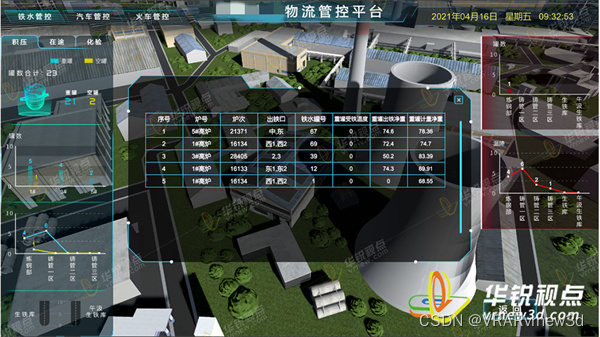
平均电压和均方根电压(RMS Voltage)
文章目录
- 平均电压和均方根电压(RMS Voltage)
- 1、概述
- 2、平均电压
- 3、均方根电压(RMS Voltage)
- 4、总结
1、概述
在 DC 状态下,只能对电压值进行一种定义,该值是明确的,并且由参考值 0 V 与 DC 信号的平线图之间的差异确定。然而,在 AC 状态下, 仅提及一个电压值可能会导致混乱。 从一个简单的正弦波形,我们至少可以列出四种不同的电压定义:

峰值(Peak Value)对应于参考值(即交流信号振荡的值)与信号最大值之间的差值。 峰峰值是峰值乘以因子2,它对应于信号的总垂直宽度。
在图1中,我们还用红色突出显示了平均值和RMS值,这是我们将重点关注的本文中的两节将分别介绍平均值和RMS值,我们将了解它们是如何定义的,如何确定它们,最后我们将了解 RMS 值的特殊之处。
2、平均电压
对于基本的对称正弦波、三角波、方波或锯齿波(参见图 2 和交流波形教程),很难说清楚平均电压值,我们将在下面标记 A。 事实上,这些类型的信号在其周期的一半期间为正,在另一半期间为负。 换句话说,信号 50% 的时间位于水平轴上方,50% 的时间位于水平轴下方。根据该观察,很容易理解,如果我们考虑整个周期上任何这些信号的平均值,则为 等于 0,无论峰值如何,因此不相关。

我们可以通过解释如何计算平均值来证明这个结果。 对于有限的一组值,平均过程包括将所有值(V1、V2、V3…)相加,然后除以该组的基数 N(该组中有多少个值):

然而,对于模拟信号来说,不可能简单地对信号在一个周期内获取的所有瞬时值(也称为中坐标)求和,因为存在无穷大。 我们不使用求和,而是使用积分运算:

对于如图 1 所示的基本波形,我们可以看到该公式的第一项和第二项相等但符号相反,因此平均值等于 0。
为了使这些信号的平均值有意义,我们更愿意分别考虑半个正周期和半个负周期,它们的一些值分别在下图 3 中以红色和绿色突出显示:

与公式 1 类似,我们可以分别定义正半周期 (A+) 和负半周期 (A–) 的平均值:

A + A_+ A+和 A – A_– A–的值取决于我们正在处理的信号及其各自的峰值 ( V p V_p Vp)。 我们在下面列出了绝对值 |A| 最常见的基本和对称交流信号的 A + A_+ A+ 和 A – A_– A–:
- 正弦波:|A|=0.637× V p V_p Vp
- 三角波:|A|=0
- 方波:|A|= V p V_p Vp
- 锯齿波:|A|=0.5× V p V_p Vp
我们可以这样总结本节:当我们想要平均信号时,如果该过程是在整个周期或更小的值上完成的,我们需要给出精度。 对于基本和对称的交流信号,无论频率、峰值或周期如何,对整个周期求平均的结果始终为 0 V。 因此,对这些信号的半周期进行平均更为合适。
3、均方根电压(RMS Voltage)
RMS(Root Mean Square) 代表均方根,它与前面介绍的平均值的运算类似,但对瞬时值进行平方,并对总分数求根:

出于与前面所述相同的原因,我们使用积分运算来定义模拟信号的 VRMS:

与平均值不同,RMS 值始终是针对信号的整个周期定义的,确定该值确实不会产生混淆。
作为示例,让我们确定峰值 V p V_p Vp 和角度的正弦波形的 RMS 值 角动量 ω V ( t ) = V p × sin ( ω t ) ω V(t)=V_p\times \sin(ωt) ωV(t)=Vp×sin(ωt)。 我们记下 f 是满足 f = ω / 2 π f=ω/2π f=ω/2π 和 T = 1 / f T=1/f T=1/f 周期的频率。
首先,我们计算我们记下的积分项 I:

我们用三角恒等式 s i n 2 ( x ) = ( 1 − c o s ( 2 x ) ) / 2 sin^2(x)=(1-cos(2x))/2 sin2(x)=(1−cos(2x))/2继续:

计算 0 和 T 之间的括号项得出 2 π / ω = T 2π/ω=T 2π/ω=T。 因此,积分项最终等于 ( π V p 2 ) / ω (πV_p^2)/ω (πVp2)/ω。 从公式4 中我们可以看出,我们仍然需要乘以 1 / T 1/T 1/T,这会导致根下的项为 [ ( π V p 2 ) / ω ] × [ ω / ( 2 π ) ] = V p 2 / 2 [(πV_p^2)/ω]×[ω/(2π)]=V_p^2/2 [(πVp2)/ω]×[ω/(2π)]=Vp2/2。
最后,求根后,正弦波形的 RMS 值的最终表达式为:

我们在下面列出了可以通过与上一节所述的基本信号和对称信号的正弦示例相同的方法计算的 RMS 值:
- 正弦波: V R M S = V p / √ 2 V_{RMS}=V_p/√2 VRMS=Vp/√2
- 三角波和锯齿波: V R M S = V p / √ 3 V_{RMS}=V_p/√3 VRMS=Vp/√3
- 方波: V R M S = V P V_{RMS}=V_P VRMS=VP
需要注意的是,VRMS>|A|,RMS值总是大于平均值的绝对值。
了解 RMS 值的基础是,它根据下图 4 在直流和交流状态之间创建了联系:

注意:电压和电流的 RMS 值是在直流状态下在电阻上产生相同功率的值。
4、总结
现代电压表或示波器可以轻松测量平均值和 RMS 值,并提供有关交流信号的信息。
平均值的数值方法包括对信号的所有值求和并将总和除以值的数量。 对于真实信号,我们更喜欢使用积分运算,它是无限组值的总和的扩展。
平均值可以有两种定义,具体取决于平均值是在整个周期还是半周期上进行的。 对称信号的特征是整个周期的平均值为 0。 仅当信号中存在直流分量或者信号围绕水平参考不对称时,全周期的平均值才不同于 0。 还可以对半周期进行平均,以便表征不同的对称信号。
RMS 值的定义与平均值类似,但每个总和值均取平方且最终结果求根。 均方根值始终高于平均值的绝对值,并在交流和直流状态之间建立了联系,这就是工程师特别使用它的原因。