摆动序列

力扣链接

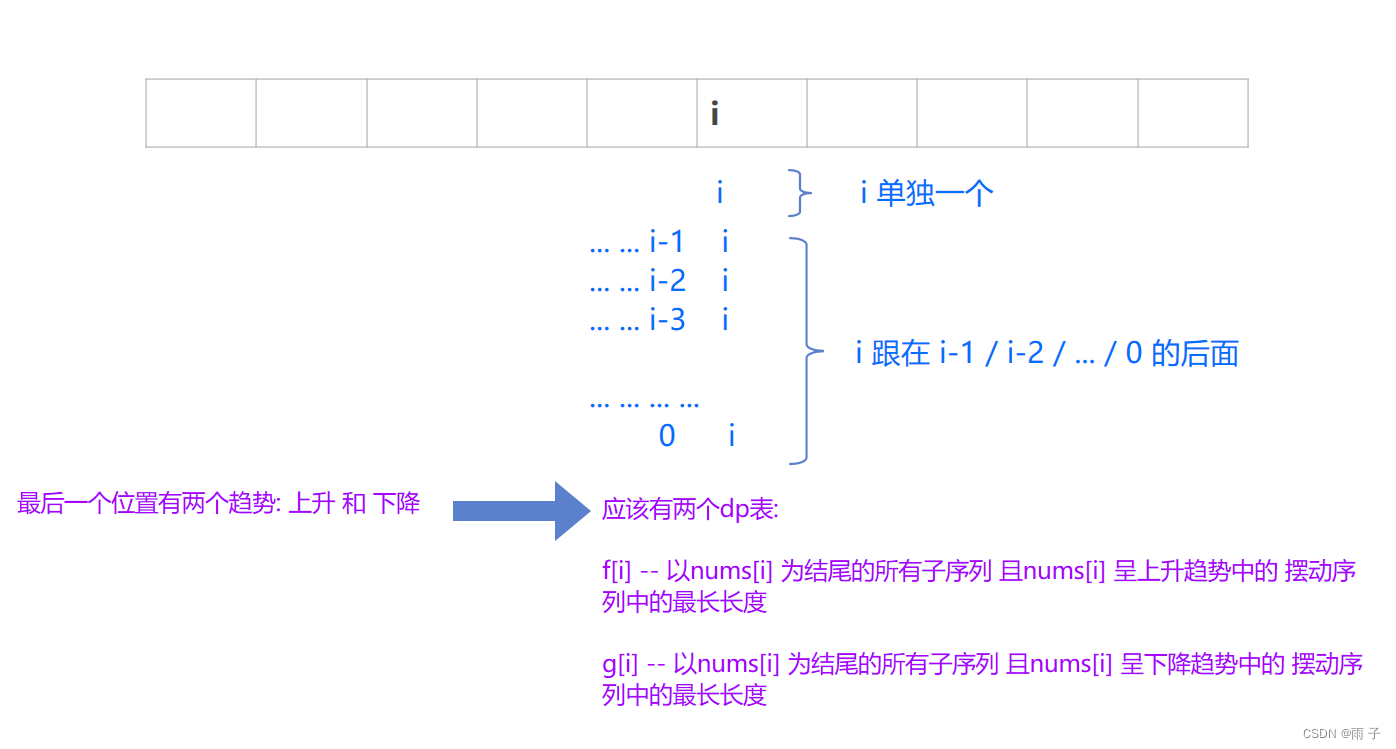
• 子序列 ⇒ dp[i]的含义: 以nums[i] 为结尾的所有子序列中的 摆动序列中的最长长度
• 子序列 ⇒ 状态转移方程: 最后一个元素的构成
  
  
• 初始化: 都初始化为 1
• 遍历方向: 从前往后
• 返回结果: f表 和 g表中的最大值

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) 
    {
        int n = nums.size();

        // 建表 + 初始化
        vector<int> f(n,1 ), g(n, 1);

        int res = 1;
        for(int i = 1; i < n; i++)
        {
            for(int j = 0; j < i; j++)
            {
                if(nums[i] > nums[j])
                    f[i] = max(g[j] + 1, f[i]);
                else if(nums[i] < nums[j])
                    g[i] = max(f[j] + 1, g[i]);
            }

            res = max(res, max(f[i], g[i]));
        }

        return res;
    }
};

---

最长递增子序列的个数

力扣链接

首先, 先分享一下我做这个题目的 新路历程:
最长递增子序列的个数, 这不就是最长递增子序列的长度的翻版题嘛
先用动态规划求得 以每一个下标结尾的最长递增子序列的长度, 同时 所有长度中的最长长度, 记作max_len
然后再 遍历dp表, 统计 dp[i] == max_len 的个数 res, 返回res即可.👇👇👇

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> dp(n,1);

        int max_len = 1;
        for(int i = 1; i < n; i++)
        {
            for(int j = 0; j < i; j++)
            {
                if(nums[i] > nums[j])
                    dp[i] = max(dp[i], dp[j] + 1);
            }

            // dp表中的最大长度
            max_len = max(max_len, dp[i]);
        }

        // 统计结果
        int res = 0;
        for(auto e : dp)
        {
            if(e == max_len)
                res++;
        }

        return res;
    }
};

就拿示例1: [1, 3, 5, 4, 7] 来说, 最长递增子序列的长度是 4, 分别是 [1, 3, 4, 7] 和 [1, 3, 5, 7]
这两个子序列都是 以同一个位置结尾的, 按照我们上面的想法, 其实是 只算了一遍的!!!

我们应该在统计最长子序列的长度的同时, 也要统计最长子序列的个数
故, 我们应该有两个状态方程:
len[i] — — 以nums[i] 为结尾的子序列中, 最长子序列的 长度
count[i] — — 以nums[i] 为结尾的子序列中, 最长子序列的 个数

• 状态转移方程:

  • 铺垫知识: 遍历一次 返回区间内的最大值 及 最大值出现的次数 ?
  • 
    
    

• 初始化: len表 和 count表都初始化为最差情况, 即都初始化为 1

• 遍历方向 : 从前往后

• 返回结果 : 返回count表中最大值出现的次数, 这个时候又可以用上面的想法
  

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) 
    {
        int n = nums.size();

        // 建表 + 初始化
        vector<int> len(n, 1), count(n, 1);

        // 统计最后的结果
        int retmax = 1, retcount = 1;

        for(int i = 1; i < n; i++)
        {
            for(int j = 0; j < i; j++)
            {
                if(nums[i] > nums[j])
                {
                    if(len[i] == len[j] + 1)
                    {
                        count[i] += count[j];
                    }
                    else if(len[j]  + 1> len[i])
                    {
                        len[i] = len[j] + 1;
                        count[i] = count[j];
                    }
                }
            }

            // 统计最后的结果
            if(retmax == len[i])
                retcount += count[i];
            else if(retmax < len[i])
            {
                retmax = len[i];
                retcount = count[i];
            }
        }

        return retcount;
    }
};

---

问世间情是何物？直教生死相许.
— — 元好问· 《摸鱼儿•雁丘辞》