要点

Batch Normalization

• 训练

若batchsize=64,某一层的某一个神经元会输出64个响应值，对这64个响应值求均值，标准差，然后标准化，对标准化的结果乘$\lambda +\beta$,其中$\lambda$和 $\beta$是需要训练的参数，并且每一个神经元都有一组$\lambda$和 $\beta$。
如此操作，即可把神经元的输出限制在$N(0,1)$标准高斯分布之中。

• 测试

与训练进行相同处理，只不过不再需要训练均值$u$、方差$\sigma$、$\lambda$和 $\beta$参数，这两个参数的值由训练期间的全部$\lambda$和 $\beta$求出，如$u_{test}=E(u_{batch})$,$\sigma =\frac{n}{n-1}E({\sigma }_{batch}^2)$.

使用batch normalization可以加快训练收敛，改善梯度，尽可能不处于饱和区，如使用sigmoid激活函数，在（0,+1）(-1,0)之间处于不饱和。

Anchor

• 将一张图片划分为$13\ast 13$的网格，即169个grid cell,每一个grid cell设置固定数量（n=5）与大小的anchor，每一个anchor的长宽等大小不同,并且与真实框IOU最大的anchor负责预测该grid cell负责的检测对象。anchor的原理类似于RCNN中存在的候选框，存在anchor，只需要每次训练预测框相对于anchor的偏移量即可。
• 在预测阶段，输出的向量对每一个anchor都有预测对象类别概率值，相对于yolov1只有每个grid cell才有类别概率。一个grid cell有5个anchor，每个anchor有$（x,y,w,h,confidence,20kindsofclasses）$。

细粒度特征

passthrough 层，将高分辨率的特征图与低分辨率的特征图融合在一起，实现多尺度的检测效果，启发于SSD检测。
例如一张特征图矩阵，大小为4*4*3,按照下方方式进行重组

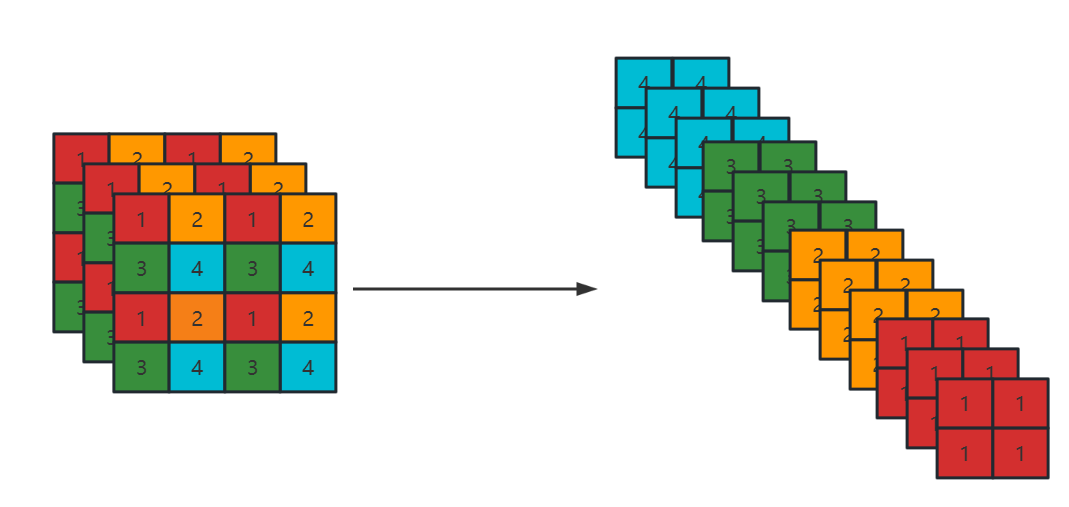
图中通道数变为4倍，大小为原来的1/4，$4\ast 4\ast 3$ --> $2\ast 2\ast 12$
将经过处理得到的特征图与原特征图经过卷积处理结果进行融合。
在实际的yolov2中，网络层中有一个$26\ast 26\ast 512$的特征图，一方面进行使用64个$1\ast 1$卷积，得到$26\ast 26\ast 64$的特征图，然后将该$26\ast 26\ast 64$的特征图送入 passthrough 层，得到$13\ast 13\ast 256$的特征图;另一方面继续进行卷积，最后得到$13\ast 13\ast 1024$的特征图，将$13\ast 13\ast 1024$特征图与$13\ast 13\ast 256$特征图进行合并，得到$13\ast 13\ast 1280$特征图，再输入到网络中即可。

损失函数

上式中求和的$i,j,k$表示$13\ast 13$grid cell的每一个$ancho{r}_k$;

第一行为anchor与真实框的IOU交并比是否满足给定阈值，满足则计算，否则不计算该项。$-b_{ijk}^0$表示该预测框不负责预测物体的置信度，越小越好。

第二行为判断是否是前12800次迭代，是则优化anchor与预测框的位置信息，使每一个anchor确定不同的自身作用，模型稳定。

第三行为负责检测物体的anchor进行该计算：其中的三个表达式分别为真实框与预测框的定位误差，真实框与anchor的IOU值和预测框置信度的误差，真实框的类别与预测框的类别误差。