一、scrapy是什么：Scrapy是一个为了爬取网站数据，提取结构性数据而编写的应用框架，可以应用在包括数据挖掘，信息处理或存储历史数据等一系列的程序
二、scrapy的安装：pip install scrapy -i https://pypi.douban.com/simple
三、scrapy项目的创建以及运行
1.win+r 进入终端
cd C:\Users\malongqiang\PycharmProjects\pythonProject\ 爬虫练习1018
注意：路径最好是你python代码放置路径（cd + 选中文件夹拉入终端）
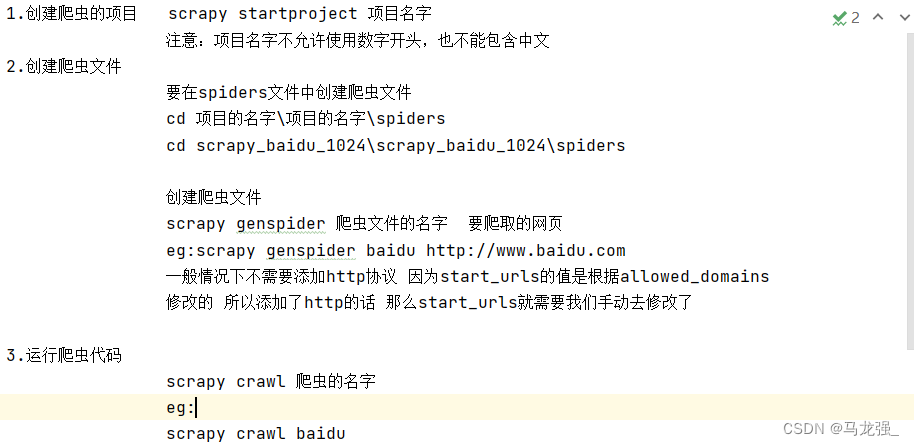
2.创建scrapy_baidu_1024文件：scrapy startproject scrapy_baidu_1024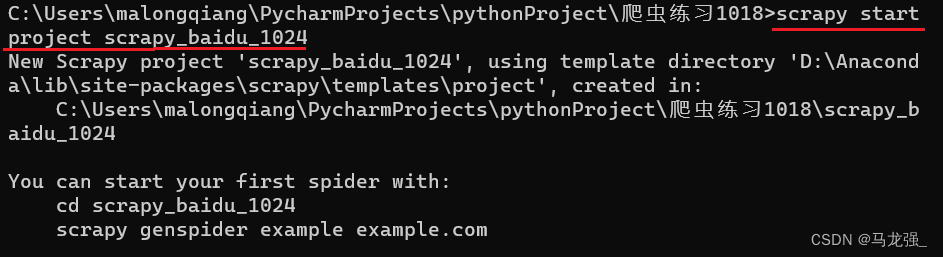
3.创建后的结果：
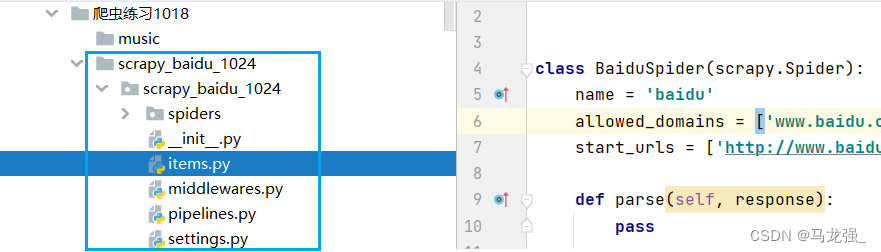4.进入spiders文件夹下：cd scrapy_baidu_1024\scrapy_baidu_1024\spiders
5.创建爬虫文件baidu.py：scrapy genspider baidu http://www.baidu.com
6.baidu.py的内容：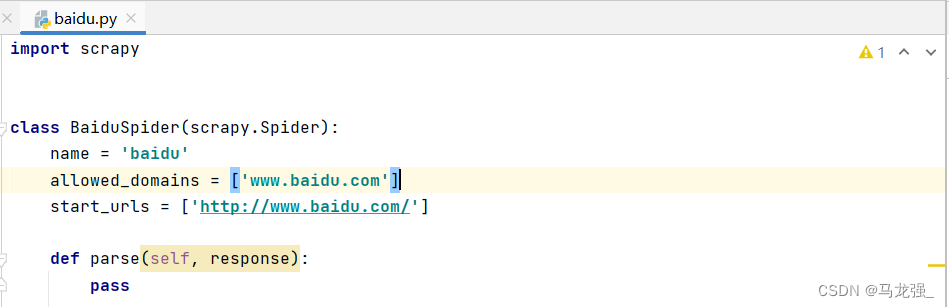
7.写入要打印的内容：my love
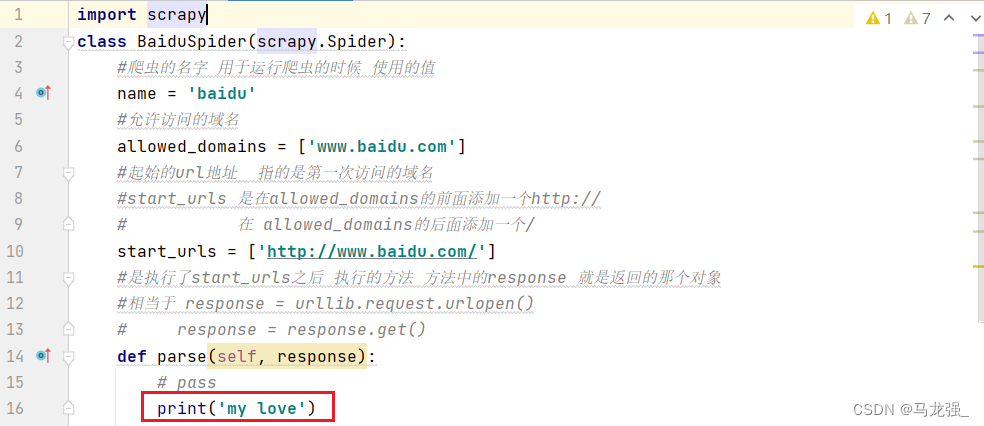8.运行爬虫文件(baidu):scrapy crawl baidu
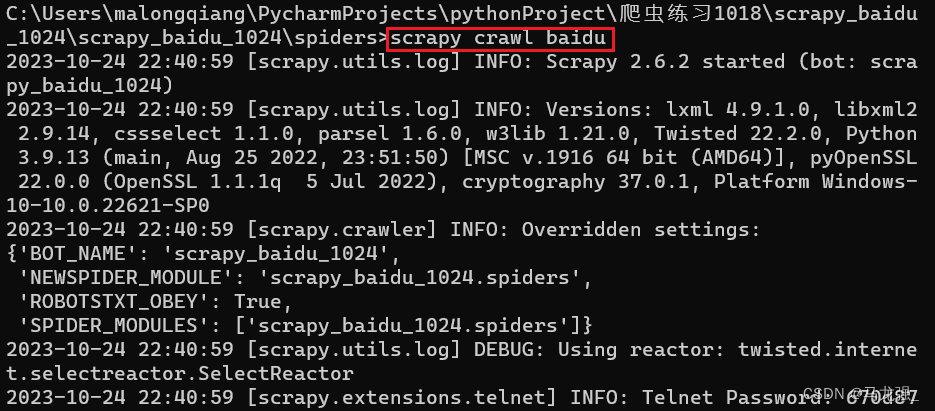9.没有结果，爬取失败，原因如下：robots.txt协议不让爬
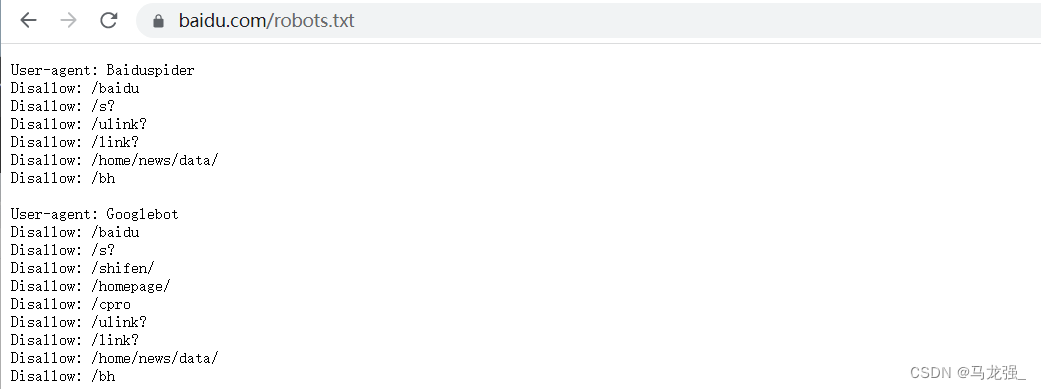10.解决办法：找到该目录下的settings注释ROBOTSTXT_OBEY = True
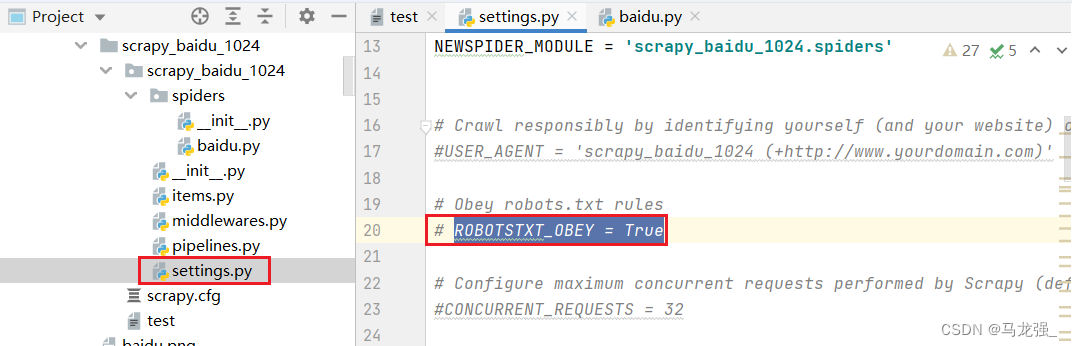11.重新运行指令,打印出来结果
四、scrapy相关内容资料:
