蜣螂优化(DBO)求解置换流水车间调度问题(PFSP)

先做一个声明：文章是由我的个人公众号中的推送直接复制粘贴而来，因此对智能优化算法感兴趣的朋友，可关注我的个人公众号：启发式算法讨论。我会不定期在公众号里分享不同的智能优化算法，经典的，或者是近几年提出的新型智能优化算法，并附MATLAB代码。

车间调度问题来自于实际的车间生产过程，根据加工过程的不同可以大致分为：单机调度(Single machine scheduling problem， SMSP)、并行机调度问题(Parallel machines scheduling problem, PMSP)、流水车间调度问题(Flow-shop scheduling problem, FSP)、作业车间调度问题(Job-shop scheduling problem, JSP)和开放车间调度问题(Open-shop scheduling problem, OSP)和。其中，流水车间调度问题(Flow-shop scheduling problem, FSP)是实际生产过程中最为常见的调度模型，广泛应用于交通运输、物流、车间生产等领域。求解FSP的方法主要分为三类：精确算法、启发式算法和智能优化算法。在处理不同规模问题时，往往采用不同的算法。例如精确算法由于时间复杂度大，仅用来解决规模较小的问题。启发式算法的优势是求解速度很快，但求得的解往往较差。因此，目前求解流水车间调度问题大多采用智能优化算法。

研究表明接近四分之一的制造、装配、服务或信息处理设施都可以视为流水车间。已经证明，当机器数m>2时，流水车间调度问题是一个强NP-hard问题。由于其在学术与工程应用中的重要性，它获得了广泛的关注与研究。FSP一般描述为：n个工件在m台机床上加工，每个工件包含h道工序，每道工序分配到不同的机床上加工。Oij表示第i个工件的第j道工序，n个工件的h道工序的加工路径相同，即Machine(Oij)=Machine(Ouj)了，其中i≠u,j=1,…,h。Oij被指定在机床Mk(k=1,...,m)上加工，pijk(i=1,..,n,j=1,.,h,k=1,...,m)表示其加工时间。固定分配机床的FSP问题是一般流水车间调度问题，每道工序被唯一指定在一台机床上加工，机床不能选择，即h=m，FSP调度任务是确定各个工件的加工次序，其目标是最大完成时间最小化。

FSP假设如下：

(1)所有工件在零时刻都准备就绪，而且工件在机器上的加工时间是确定的；

(2)每个工件加工路径相同，不允许改变；

(3)每个时刻，每台机床只能加工一道工序，工序不允许中断；

(4)一个工件不能同时在不同机床上加工；

(5)工序的准备时间忽略不计，或者包含在加工时间中，机器之间的缓冲区足够大

01
问题介绍

置换流水车间调度问题(Permutation flow-shop scheduling problem, PFSP)是流水车间调度问题(FSP)的简化模型，通常描述为n个工件J={1,...,n}在m台机器M={1,...,m)上加工，每台机器上各工件的加工顺序相同，给定工件i(i∈J)在机器j(j∈M)上的处理时间pij，目标是求得一个工件加工顺序使得某个调度目标达到最优，常用的调度目标是最大完工时间Cmax最小或总流经时间最小。

PFSP的假设如下：

(1)所有工件在零时刻都准备就绪，而且工件在机器上的加工时间是确定的；

(2)每个工件加工路径相同，不允许改变；

(3)每个时刻，每台机床只能加工一道工序，工序不允许中断；

(4)一个工件不能同时在不同机床上加工；

(5)工序的准备时间忽略不计，或者包含在加工时间中；

(6)不允许作业抢占，即在每台机器上工件一旦开始加工则不能中断，工件加工顺序在所有机器上一致。

可以发现，PFSP和FSP的本质区别在于：PFSP要求每个工件在每台机器上的加工顺序相同，如图1所示。这样一来，可知对于n工件、m台机器而言，一般流水车间调度问题(FSP)的解空间规模为(n!)^m，而置换流水车间调度问题(PFSP)的解空间规模为n!。尽管PFSP的解空间规模远小于FSP，但已证明m≥3的PFSP即为NP-hard问题。

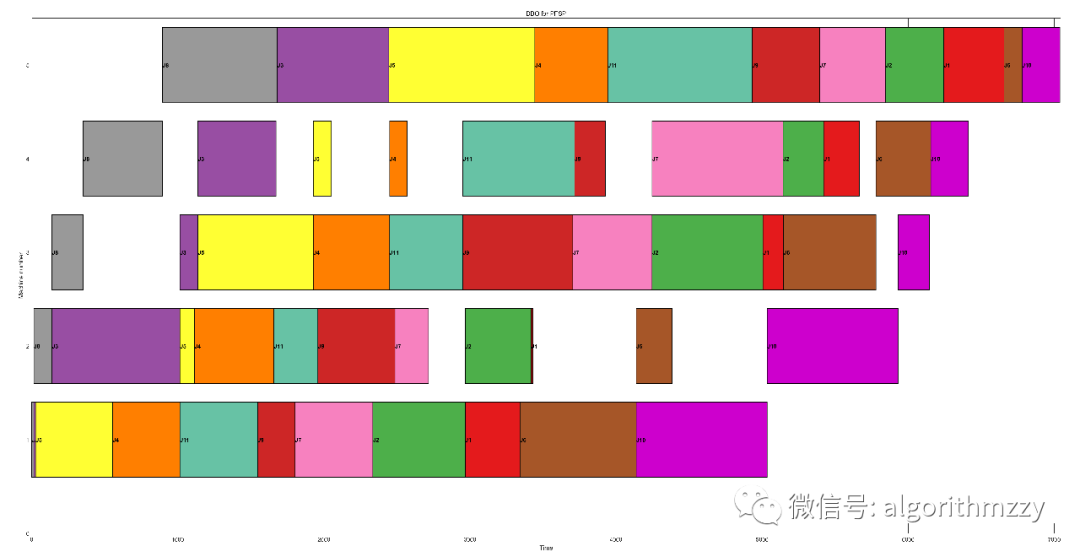
图1 11工件×5机器的PFSP甘特图举例，所有工件Ji在每台机器上的加工顺序一致

02
问题模型

与往期推送一样，公众号里不方便编辑数学公式。因此，这部分内容做成图片导入。图片截自一篇博士学位论文：

[1]刘延风. 置换流水车间调度问题的几种智能算法[D].西安电子科技大学,2013.

03
编码解码

PFSP是要解决一组工件的加工排序问题，即它是一种组合优化问题，属于离散优化。而蜣螂优化(DBO)算法本身是针对连续优化问题而提出的，因此这就需要设计候选解的编码与解码方式。

Li等提出的最大排序值法(Largest rank value, LRV)是将连续值映射成离散排列常用的方法之一。因此，本采用LRV规则将DBO种群中表示候选解个体的一组连续的优先值映射为离散的工件排序，如图2所示，LRV将代表种群个体的一组连续值按降序排列生成一组工件排序。(参考文献：[2] LI X, YIN M. An opposition-based differential evolution algorithm for permutation flow shop scheduling based on diversity measure [J]. Advances in Engineering Software, 2013, 55(8): 10-31.)

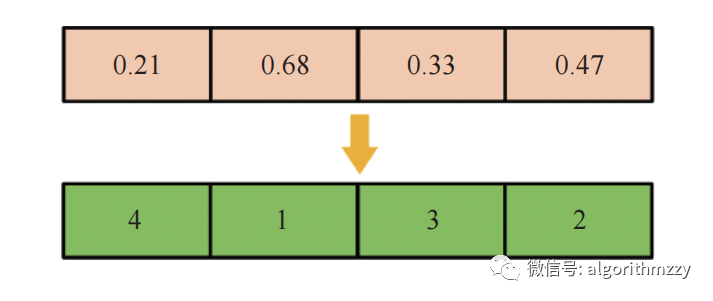
图2 最大排序值法的表示方法

04
DBO求解PFSP的流程

关于DBO算法的介绍，可翻看之前的推送，这里不再赘述。

蜣螂优化(DBO)算法(含MATLAB代码)

蜣螂优化(DBO)算法的5种最新变体(含MATLAB代码)

图3给出了DBO求解PFSP的计算流程：

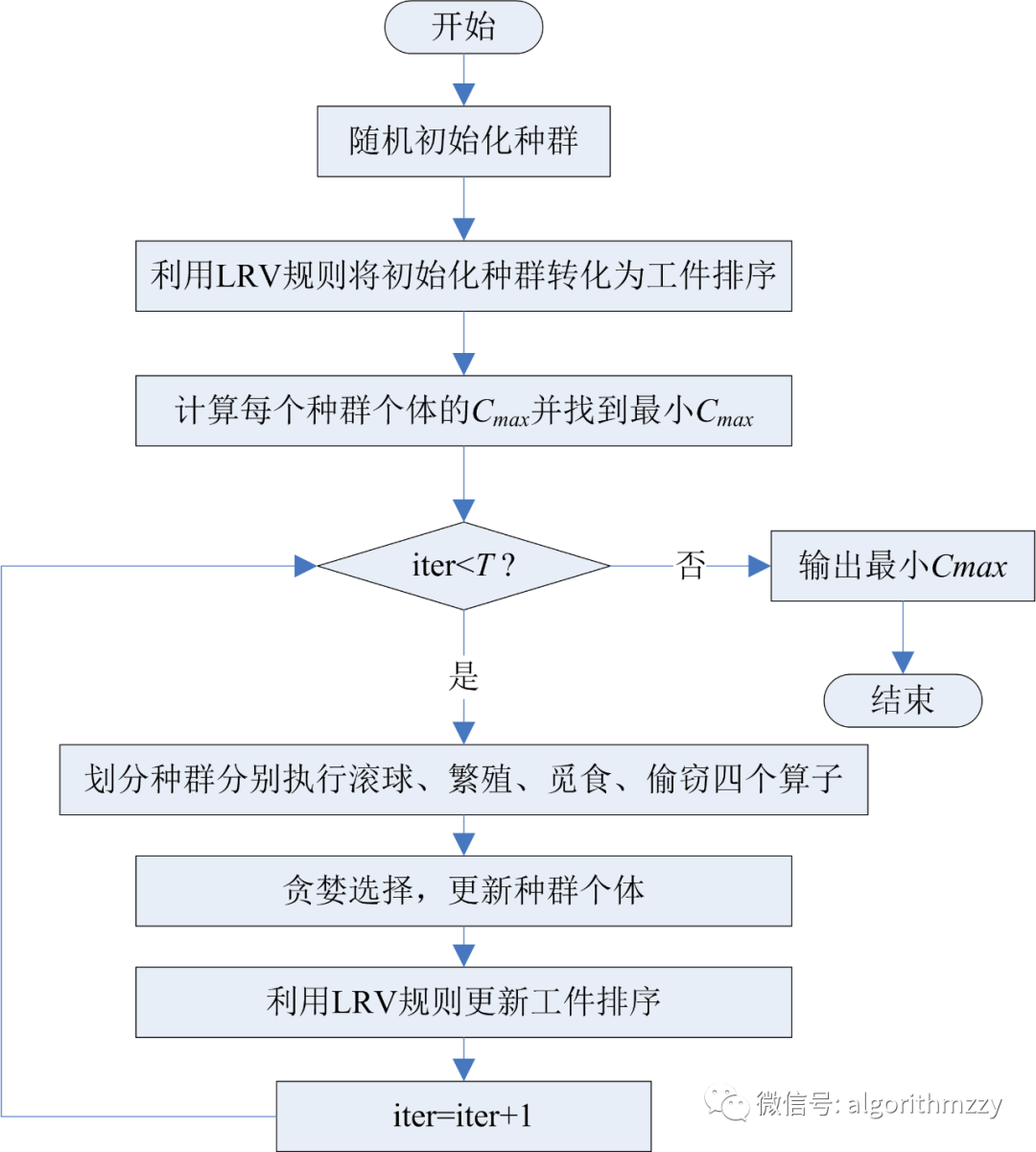
图3 DBO求解PFSP流程图

图3中，iter代表当前迭代次数，T代表最大迭代次数。

05
数值实验

对DBO求解PFSP的效果进行简单测试，调度问题算例选用Car(8个)和Rec(21个)。最大迭代次数T设置为2000，种群规模NP设为60。下面展示的结果都是算法随机运行一次得到的结果。

首先，以Car2(13工件×4机器)为例，图4绘制了种群每代的最优适宜度收敛曲线和平均适宜度收敛曲线：

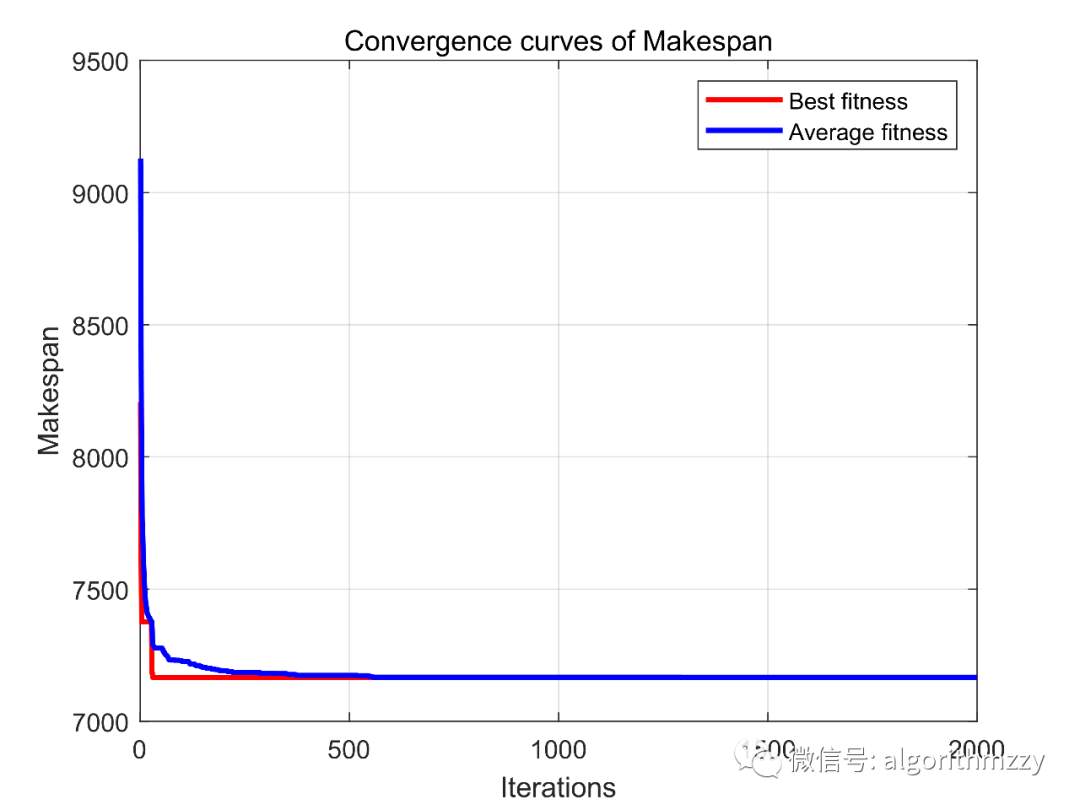
图4 DBO对于Car2的收敛曲线

图5绘制了调度结果的甘特图：

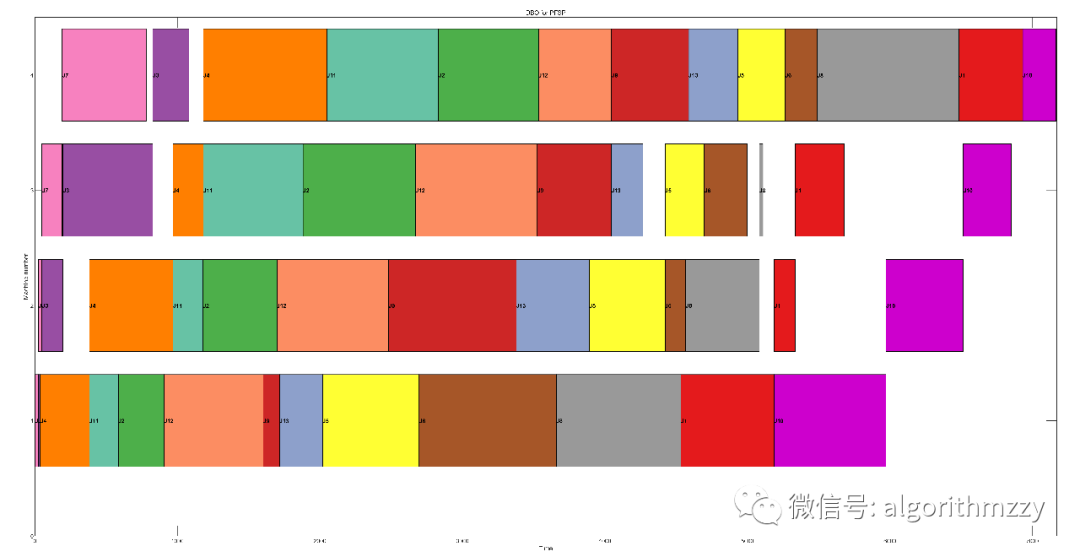
图5 DBO对于Car2的甘特图

其次，以Rec11(20工件×10机器为例)，展示DBO随机运行一次的求解结果，如图6和图7所示。

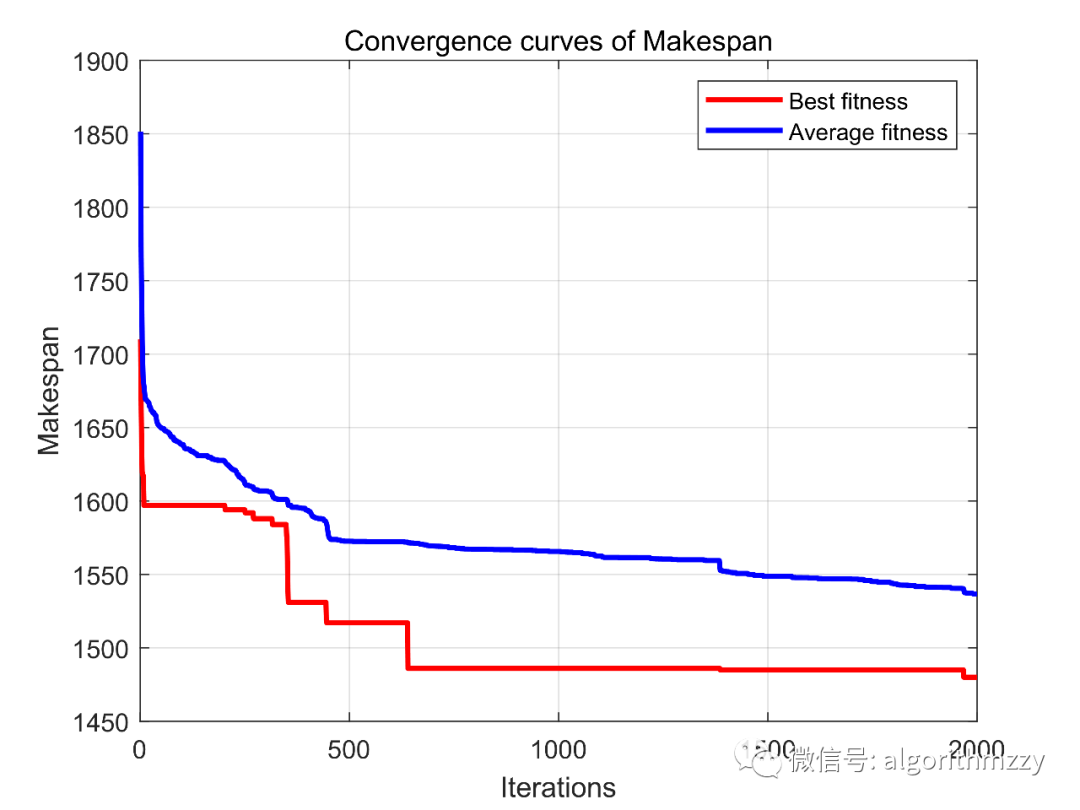
图6 DBO对于Rec11的收敛曲线

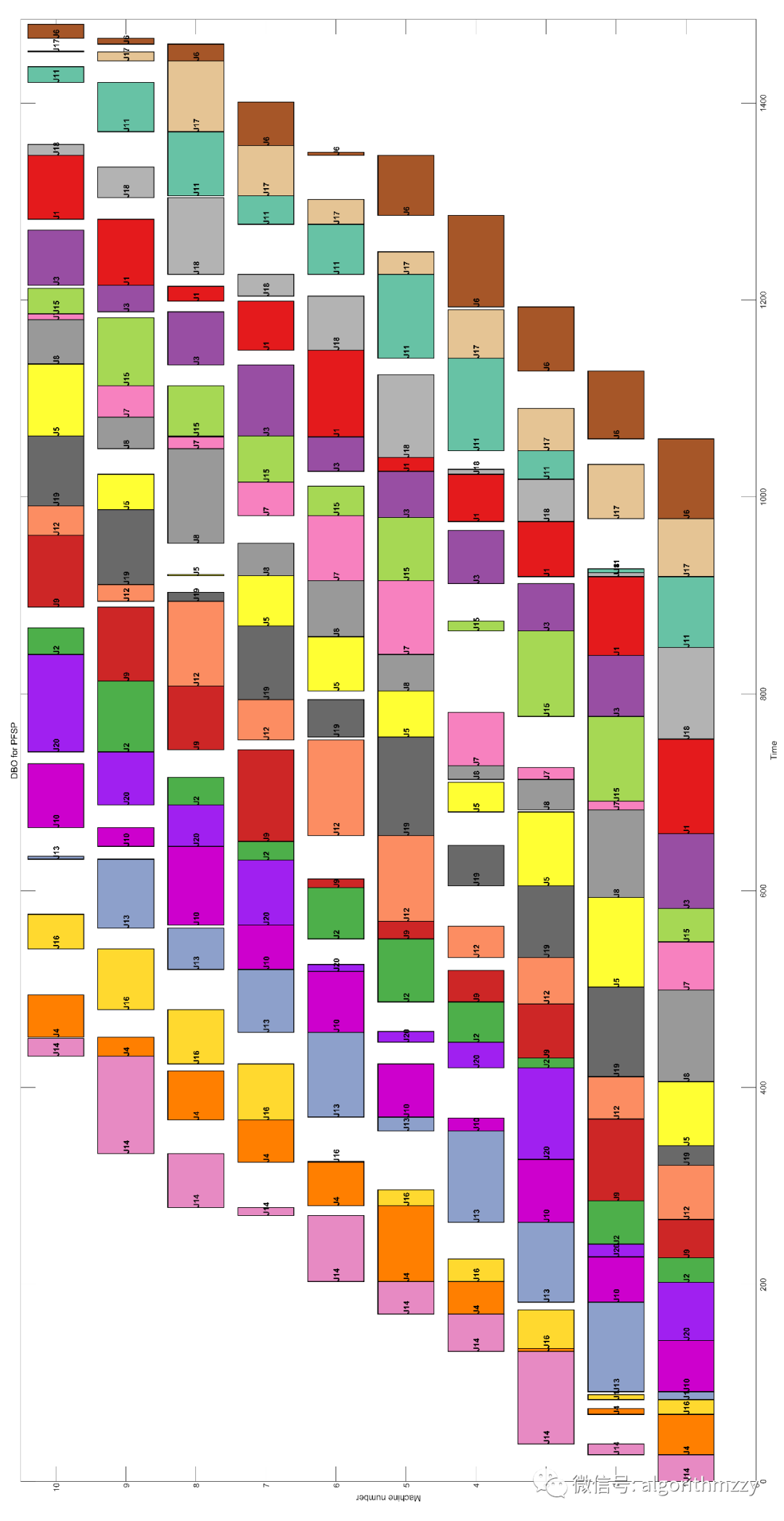
图7 DBO对于Rec11的甘特图

最后，以Rec41(75工件×20机器为例)，展示DBO随机运行一次的求解结果，如图8和图9所示。

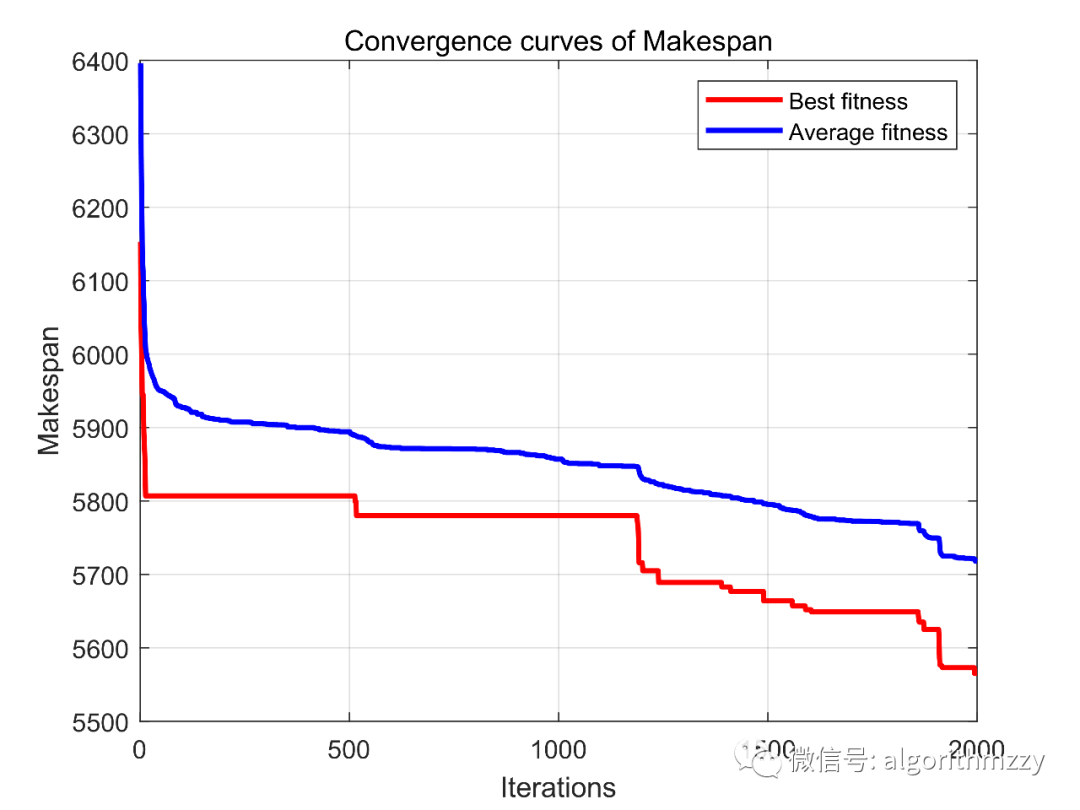
图8 DBO对于Rec41的收敛曲线

图9 DBO对于Rec41的甘特图

06
MATLAB代码

蜣螂优化(DBO)算法求解置换流水车间调度问题(Permutation flow-shop scheduling problem, PFSP)的MATLAB代码，其中：main.m是主函数，直接运行即可；DBO.m是算法的代码；color_selection用于获得甘特图的颜色配置；gantt_chart.m绘制甘特图；objective.m是目标函数，即计算Makespan；sorting.m根据调度方案计算每台机器任意时刻的加工信息(开始时间、结束时间、工件号、机器号), 用于绘制甘特图；调度算例包括Car(8个)和Rec(21个)。

输出结果包括Makespan、工件排序、计算时间、最优适宜度收敛曲线、平均适宜度收敛曲线、甘特图。

main.m主函数如下：

%%% 蜣螂优化(DBO)算法求解置换流水车间调度问题(PFSP) %%%
%%% 算法参考文献：Xue J, Shen B. Dung beetle optimizer: a new meta-heuristic algorithm %%%
%%% for global optimization[J]. The Journal of Supercomputing, 2022: 1-32. %%%
%% By 后会无期 %%
%% 2023.10.16 %%
%% 微信公众号：启发式算法讨论
%% 严格按照DBO的原始参考文献编，PFSP测试集采用Car与Rec算例(自行替换)

clear
clc

%% 数据加载
% 采用Car或Rec测试集, 自行选择测试集和实例
% Car测试集实例: Car1, Car2, Car3, Car4, Car5, Car6, Car7, Car8
% Rec测试集实例: Rec01, Rec03, Rec05, Rec07, Rec09, Rec11, ... ,Rec41
jobInfo=readmatrix('Rec.xlsx','Sheet','Rec41');  % jobInfo: 加工时间信息
jobNum=size(jobInfo,1);                          % jobNum: 工件数量
machineNum=size(jobInfo,2);                      % machineNum: 机器数量

%% 算法参数：种群数量，迭代次数
NP=60;      % 种群规模, 注意: DBO的种群规模需要设置为30的倍数
MaxIt=2000; % 最大迭代次数

tic % 计时开始
[Best_score,Best_pos,curve]=DBO(machineNum,jobNum,jobInfo,NP,MaxIt);
toc % 计时结束

disp(['Number of jobs: ',num2str(jobNum)]);              % 显示工件数
disp(['Number of machines: ',num2str(machineNum)]);      % 显示机器数
disp(['The optimal solution is: ',num2str(Best_pos)]);   % 显示最优解, 即全局最优的工件排序
disp(['The best fitness is: ',num2str(Best_score)]);     % 显示最优值, 即最小化最大完工时间

%% 绘制迭代曲线
f1=figure(1);
% 设置图片在屏幕上的位置: 显示器左下角的右侧280像素和上方400像素处
f1.Position(1:2)=[280 400];
T=1:1:MaxIt;
plot(T,curve.min,'r-','LineWidth', 2);
hold on
plot(T,curve.avg,'b-','LineWidth', 2);
grid on;
legend('Best fitness','Average fitness');
title('Convergence curves of Makespan');
xlabel('Iterations');
ylabel('Makespan');

%% 绘制甘特图
% machine_table包含每台机器任意时刻的加工信息（开始时间，结束时间，工件号，机器号）
machine_table=sorting(Best_pos,machineNum,jobNum,jobInfo); % 调用"sorting"子函数, 获得machine_table, 用于画甘特图

f2=figure(2);
% 设置图片在屏幕上的位置: 显示器左下角的右侧850像素和上方400像素处
f2.Position(1:2)=[850 400];
gantt_chart(machine_table); % 调用"gantt_chart"子函数获得配色方案, 绘制出甘特图
title('DBO for PFSP');
xlabel('Time');
ylabel('Machine number');

另外选择了九个求解PFSP的经典算法和几个近几年的高引算法。对应的MATLAB代码链接如下：

遗传算法(GA)求解PFSP	关注公众号，里面有链接
差分进化(DE)求解PFSP	关注公众号，里面有链接
粒子群优化(PSO)求解PFSP	关注公众号，里面有链接
灰狼优化(GWO)求解PFSP	关注公众号，里面有链接
鲸鱼优化算法(WOA)求解PFSP	关注公众号，里面有链接
哈里斯鹰优化(HHO)求解PFSP	关注公众号，里面有链接
麻雀搜索算法(SSA)求解PFSP	关注公众号，里面有链接
非洲秃鹫优化算法(AVOA)求解PFSP	关注公众号，里面有链接
蜣螂优化(DBO)求解PFSP	关注公众号，里面有链接
星鸦优化算法(NOA)求解PFSP	关注公众号，里面有链接
以上十种智能优化算法(GA、DE、PSO、GWO、WOA、HHO、SSA、AVOA、DBO、NOA)求解PFSP的全家桶	关注公众号，里面有链接