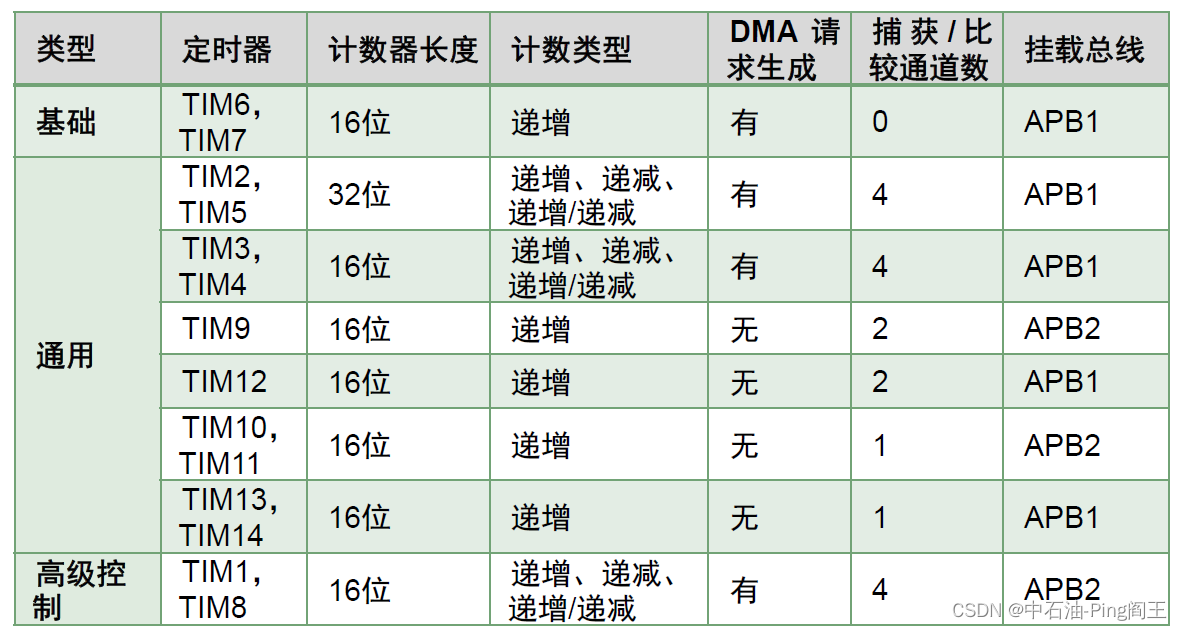
本文参考朱战力老师的数据结构与算法--使用C语言一书
文章目录
前言
一、线性表是什么?
二、具体实现
1.顺序表的定义
2.初始化ListInitiate(L)
3.求当前元素个数ListLength(L)
4.插入元素ListInsert(L,i,x)
5.删除元素ListDelete(L,i,x)
6.取元素ListGet(L,i,x)
7.小试牛刀
总结
前言
本文所介绍的内容为数据结构与算法的基础内容--顺序表操作的实现,笔者通过不断的深入学习发现,后续的数据结构中,包括堆栈、队列、串、数组、表、数和二叉树无不是通过线性表去实现,故很好的理解线性表的操作对于广大的读者来说非常的有必要!
一、线性表是什么?
线性表的抽象数据类型是线性表的逻辑结构,它表示线性表的元素、元素之间的逻辑关系以及线性表的操作集合。任何需要计算机进行管理和处理的元素都必须首先按照某种方式存储在计算机中。线性表有两种存储结构:一种是顺序存储结构,另一种是链式存储结构。一旦确定了线性表的存储结构,线性表操作集合中的所有操作就可以具体实现。
二、具体实现
1.顺序表的定义
代码如下(示例):
typedef struct {
DataType list[MaxSize];
int size;
}SeqList;其中,DataType为数组元素的数据类型,MaxSize表示数组元素的最大个数,list表示顺序表的数组成员,size表示顺序表中当前存储的数组元素个数成员,且满足条件size<=MaxSize,SeqList是结构名。
2.初始化ListInitiate(L)
代码如下(示例):
void ListInitiate(SeqList* L) {
L->size = 0;
}
说明:由于函数中要改变参数L的size域的值,因此参数L应设计为输出型参数,即参数L设计为SeqList的指针类型,否则,size域的修改值将不能带回去。
3.求当前元素个数ListLength(L)
代码如下(示例):
int ListLength(SeqList L) {
return L.size;
}
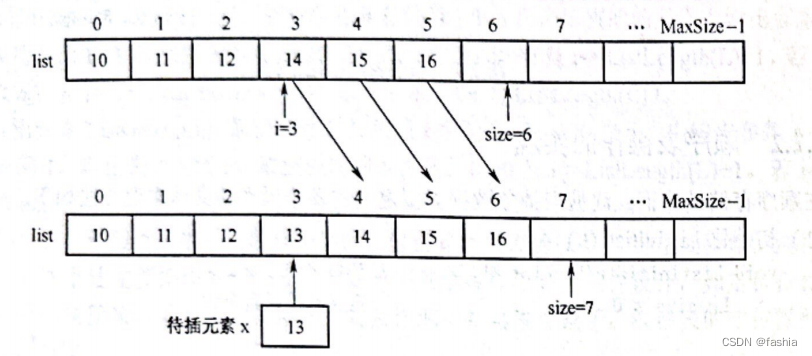
4.插入元素ListInsert(L,i,x)
代码如下(示例):
int ListInsert(SeqList* L, int i, DataType x) {
//在顺序表L的第i(0~size)个位置前插入x
//插入成功返回1,插入失败返回0
int j;
if (L->size >= MaxSize) {
printf("顺序表已满无法插入!\n");
return 0;
}
else if (i<0 || i>L->size) {
printf("参数i不合法!\n");
return 0;
}
else {
//从前向后依次后移数据,为插入做准备
for (j = L->size; j > i; j--)
{
L->list[j] = L->list[j - 1];
}
L->list[i] = x; //插入x
L->size++; //元素个数加1
return 1;
}
}
此过程中,插入成功返回1,插入失败返回0.
顺序(步骤):
(1)判断条件:
1.判断顺序表是否已满
2.判断插入的位置是否合法
(2)操作过程:
3.进行移位操作(空出插入位置)
4.直接赋值(插入)
5.使元素个数+1
图示如下:
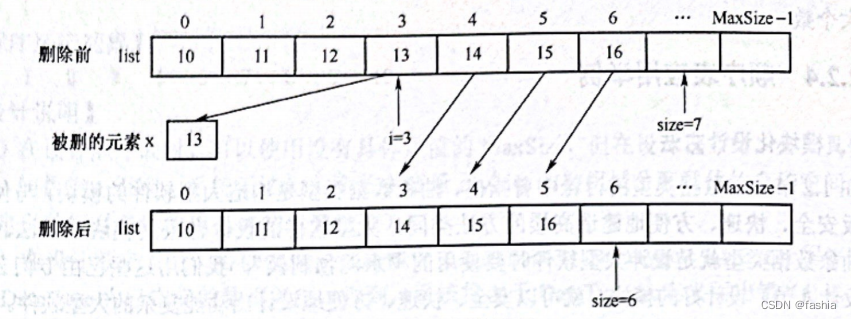
5.删除元素ListDelete(L,i,x)
代码如下(示例):
int ListDelete(SeqList* L, int i, DataType* x) {
//删除顺序表L中第i(0~size-1)个位置处的元素并保存到x中
//删除成功返回1,删除失败返回0
int j;
if (L->size <= 0) {
printf("顺序表已空无元素可删!\n");
return 0;
}
else if (i<0 || i>L->size - 1) {
printf("参数i不合法");
return 0;
}
else {
*x = L->list[i]; //保存删除元素到x中
//从前向后依次前移
for (j = i + 1; j <= L->size - 1; j++)
{
L->list[j - 1] = L->list[j];
}
L->size--;
return 1;
}
}
此过程中,删除成功返回1,删除失败返回0.
顺序(步骤):
(1)判断条件:
1.判断顺序表是否有元素可删
2.判断i是否合法
(2)操作过程:
3.使用变量x带走删除值
4.后续相应元素进行前移
5.使元素个数-1
图示如下:
6.取元素ListGet(L,i,x)
代码如下(示例):
int ListGet(SeqList L, int i, DataType* x) {
//取顺序表L中第i个元素存于x中,成功返回1,失败返回0
if (i<0 || i>L.size - 1) {
printf("参数i不合法!\n");
return 0;
}
else {
*x = L.list[i];
return 1;
}
}说明:取元素操作与删除元素操作类同,但更简单,取元素操作只需取元素list[i]到参数x中。
7.小试牛刀
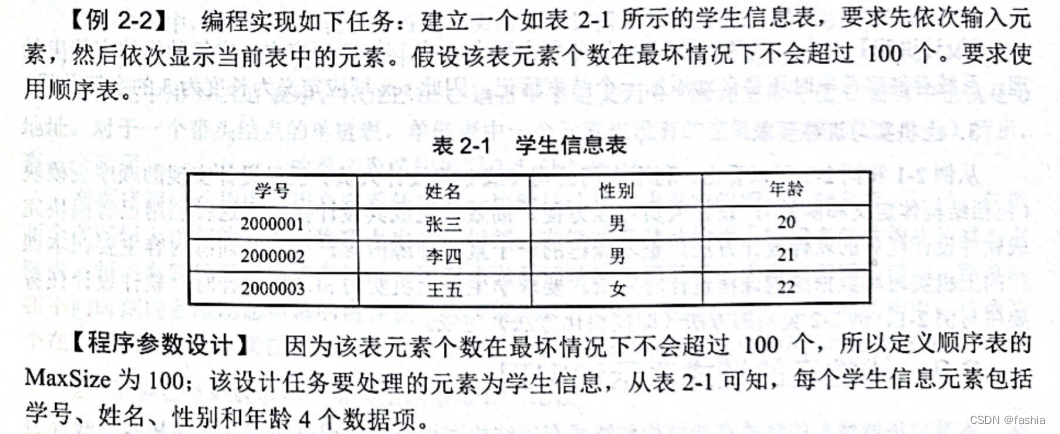
代码如下(示例):
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#define MaxSize 100
typedef struct Student {
long number; //学号数据项
char name[10]; //姓名数据项
char sex[3]; //性别数据项
int age; //年龄数据项
}StudentType; //定义学生信息结构体
typedef StudentType DataType; //定义DataType
#include"SeqList.h" //包含顺序表头文件
void main(void) {
SeqList myList;
int i;
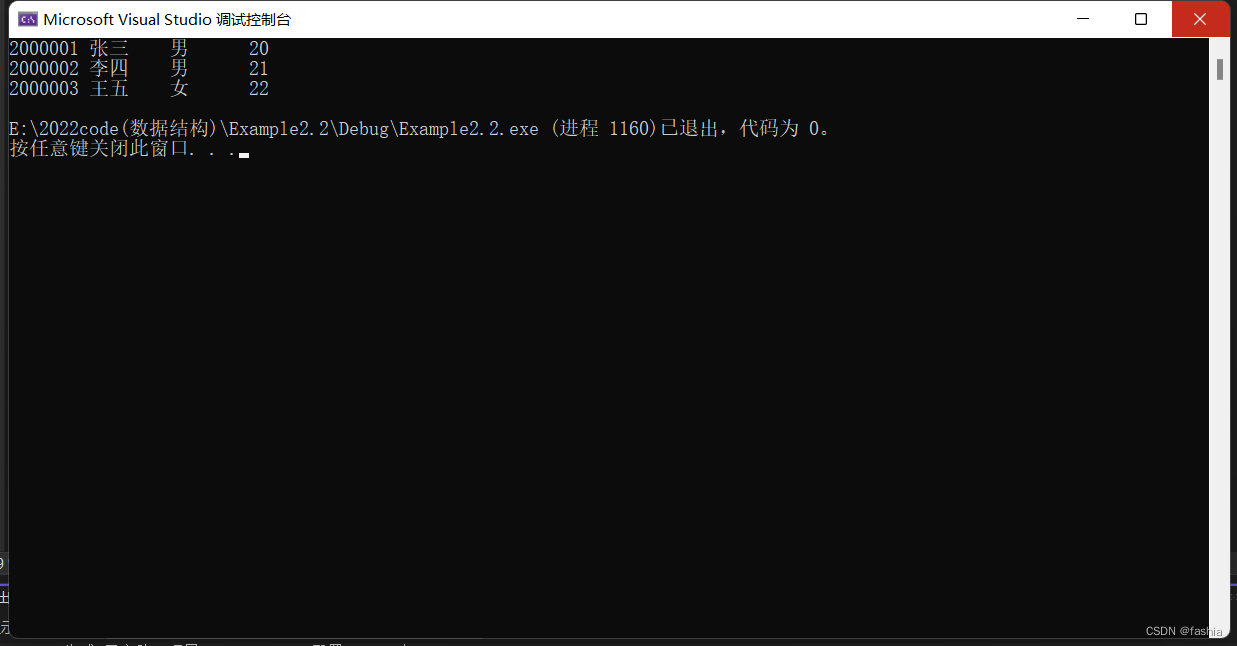
StudentType x[3] = { {2000001,"张三","男",20},{2000002,"李四","男",21},{2000003,"王五","女",22} };
StudentType s;
ListInitiate(&myList); //初始化函数调用
ListInsert(&myList, 0, x[0]); //插入函数调用
ListInsert(&myList, 1, x[1]);
ListInsert(&myList, 2, x[2]);
for (i = 0; i < ListLength(myList); i++) { //当前元素个数函数调用
ListGet(myList, i, &s); //取元素函数调用
printf("%d %s %s %d\n", s.number, s.name, s.sex, s.age);
}
}
运行结果:
总结
顺序表是一种基于顺序存储结构的数据结构,通过数组来表示元素的连续存储空间。顺序表具有快速访问任意位置的元素的优势,适用于对元素的随机访问较频繁的场景。
在顺序表中,插入和删除元素的操作可能需要移动大量的元素,导致操作的时间复杂度较高。此外,顺序表的大小是固定的,一旦存储空间被占满,就无法再插入新的元素。
总的来说,顺序表是一种简单而常见的数据结构,适用于需要快速访问元素和对存储空间连续性要求较高的场景。然而,需要注意在插入和删除操作频繁的情况下,可能会影响性能。
通过顺序表,我们可以实现元素的插入、删除、查找等基本操作,并通过下标来快速定位元素。掌握顺序表的操作,对于理解和应用其他数据结构也具有重要的意义。
通过使用顺序表,我们可以高效地组织和处理大量的数据,提高程序的运行效率和开发效率。要根据具体的需求选择合适的数据结构,以便在不同的场景中充分发挥其优势。