1 NSGA

1.1 传统多目标优化方法

1. 使用权重向量，将多目标问题转化为单目标问题：$Z={\sum }_{i=1}^N{w}_i{f}_i(x)$，$w_i$为目标的重要程度，$f_i(x)$为目标函数

所有目标权重相等会出现冲突，但是在现实需求上，需要对公式的权重优先降低以符合需求

2. 距离向量函数：
   

距离向量函数和目标权重相似，不同点在于距离向量函数需要知道每个目标函数的标，而目标权重方法则需要赋予每个目标相关重要性

3. 最大最小公式：$\min \mathcal{F}(x)=\max [{\mathcal{Z}}_j(x)]$
   

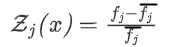
1. 适用于优先级相等的目标
2. 可以和无量纲的权重结合，以改变优先级
3. 可以和需求等级向量结合使用

1.2 多目标转为单目标的缺点

• 单目标的优化可以保证pareto最优解，但结果是单点解
• 如果某些目标有噪声或具有不连续的变量空间，这些方法可能无法有效工作。其中一些方法也很昂贵，因为它们需要在向量优化之前了解个体最优

1.3 权重向量距离说明

1. 权重向量为$(0.5,0.5)$时，说明要求$f11$和$f12$同时兼顾较小，故解为$x=1$
2. 权重向量为$(1,0)$时，说明更加强调$f11$小，因此此时的解为$x=0$
3. 权重向量为$(0,1)$时，说明更加强调$f12$小，因此此时的解为$x=2$

如果想获得图中$(0,2)$之间特殊的Pareto可行解必须要知道权重，但是这个区间的Pareto解对应的权重不易获取

1.4 NSGA方法

1.4.1 流程

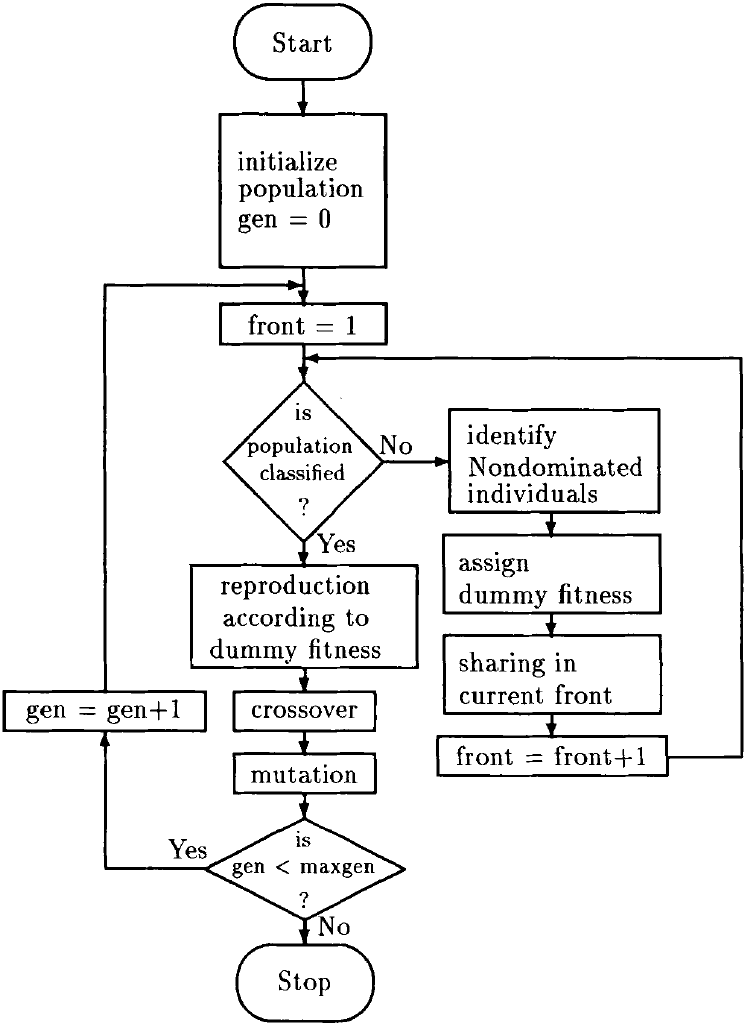
1.4.2 关键步骤

1. 对于$f_1,f_2$均为最小化问题，如果$f_1(i)<f_1(j)and{f}_2(i)<f_2(j)$，则$i$支配$j$

# 选择排序
def non_sort(matrix):
    realValue = binaryDecode(matrix)
    # realValue = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
    # y1[j] < y1[i] and y2[j] < y2[i] 说明j支配i
    ranks = []  # 等级列表
    y1 = np.array(f1(realValue))
    # y1 = np.array([2, 3, 3, 4, 4, 5, 5, 5, 6])
    y2 = np.array(f2(realValue))
    # y2 = np.array([7.5, 6, 7.5, 5, 6.5, 4.5, 6, 7, 6.5])
    while True:
        rank = []   # 同一等级的元素列表
        indexs = []   # 记录当前非支配的索引
        for i in range(y1.size):
            nondominated = True  # 当前元素知否被其它元素所支配
            for j in range(y1.size):
                if y1[j] < y1[i] and y2[j] < y2[i] and i != j:
                    nondominated = False     # i被j支配
                    break
            if nondominated == True:
                rank.append(realValue[i])
                indexs.append(i)

        if len(rank) > 0:
            ranks.append(rank)

        # 移除已经分好等级的元素
        y1 = np.delete(y1, indexs)
        y2 = np.delete(y2, indexs)
        realValue = np.delete(realValue, indexs)

        if y1.size == 0:
            break

    return ranks

2. 求小生境$niche$
   $$Sh(d_{ij})=\{\begin{array}{ll}1-(\frac{d_{ij}}{{\sigma }_{share}}{)}^2& d_{ij}<{\sigma }_{share}\\ 0& else\end{array}$$

A parameter niche count is calculated by adding the above sharing function values for all individuals in the current front.

$$nicheCount=\sum _i^{N-1}Sh$$

# 求当前等级中各元素小生境的个数，在目标空间上共享
def niche(rank):
    l = len(rank)
    counts = [0] * l
    y1 = f1(np.array(rank))
    y2 = f2(np.array(rank))
    # x = np.array(rank)
    for i in range(l):
        for j in range(l):
            if i == j:
                continue
            dij = math.pow((y1[i] - y1[j]) ** 2 + (y2[i] - y2[j]) ** 2, 0.5)
            # dij = math.fabs((x[i] - x[j]))
            if dij < shareDistance:
                counts[i] += 1 - (dij / shareDistance) ** 2
    return counts

共享可以在参数上共享也可以在目标上共享

3. 求个体适应度值
$fitness=\frac{dummyFitness}{nicheCount}$

def fitness(ranks):
    dummyFitness = 1
    fits = []
    for rank in ranks:
        counts = niche(rank)
        for count in counts:
            if count == 0:
                fit = dummyFitness
            else:
                fit = dummyFitness / count
            fits.append(fit)
        dummyFitness = dummyFitness - 1/len(ranks)
    return fits

1.5 注意

1. ${\sigma }_{share}$需要指定，指定的不合适收敛比较难
2. 在参数上共享容易提早收敛，在目标上共享会使得目标值具有多样性，但是参数变量不具有多样性。
3. 种群太小，导致非支配解过少；种群太大，容易提早收敛
4. 随着$rank$变大，$dummyFitness$ 减小。$dummyFitness$ 是自己指定的

2 NSGA-II

2.1 NSGA的缺点

1. 非支配排序计算复杂度高
2. 缺乏精英策略
3. 需要指定合适的共享参数${\sigma }_{share}$

2.2 NSGA-II在NSGA上的变动

1. 采用了快速的非支配排序(精英主义)，以达到快速收敛的目的
2. 采用拥挤度，为了使得pareto解具有多样性

2.3 NSGA-II流程

1. 父代子代混合
   
   

2. 对混合后的个体计算两个值：$n_p和Se{t}_p$
   

3. 对混合后的个体进行非支配排序
   

4. 计算拥挤度
   $i{<}_{n}j$表示$i$拥挤度支配$j$
   $$\begin{gathered} i{<}_{n}j满足下面至少一个条件 \\ {i}_{rank}<j_{rank}条件1 \\ {i}_{rank}=j_{rank}and{i}_{distance}>j_{distance}条件2 \end{gathered}$$
   将当前的个体按照目标函数进行排序
   
   对于两个目标函数拥挤距离为长方形周长的$\frac{1}{2}$
   1. 不需要计算全部拥挤度，只需要按照ranks来计算，只要个数达到N，拥挤度计算就可以停止了。
   2. 要对所有目标函数归一化。
   3. 第一个和最后一个个体的拥挤度为无穷，因为这两个点只有一边有值。
   伪代码
   
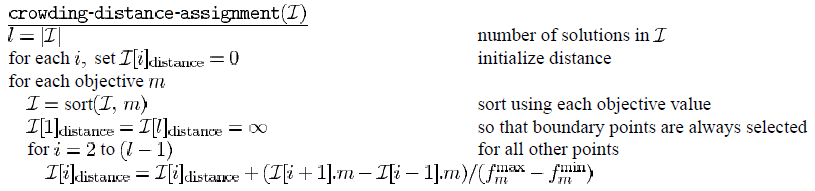
   $\mathcal{I}[i].m$：表示集合中第$i$个个体的第$m$个目标函数值
   $f_m^{max}$：表示种群中第$m$个目标函数的最大值
   $f_m^{min}$：表示种群中第$m$个目标函数的最小值

5. 相同的$rank$比较拥挤度的时候采用的是锦标赛选择算子。

   • 确定每次选择的个体数量N。（二元锦标赛选择即选择2个个体，即K = 2）
   • 从种群中随机选择K个个体(每个个体被选择的概率相同) ，根据每个个体的适应度值，选择其中适应度值最好的个体加入到下一代种群集合中。
   • 重复步骤(2)多次（重复次数为种群的大小），直到新的种群规模达到N。