大家好,我是带我去滑雪!
多变量GARCH(Generalized Autoregressive Conditional Heteroskedasticity)模型是一种用于建模多个时间序列变量之间的条件异方差性(conditional heteroskedasticity)的统计模型。它在金融、经济学和其他领域中具有广泛的用途,并具有以下用途和优点:
用途如下:
-
风险度量: 多变量GARCH模型用于度量多个资产或变量之间的风险,有助于投资者和决策者了解不同资产之间的相关性和波动性。这对于风险管理和投资组合优化至关重要。
-
资产组合优化: 在资产配置和投资组合管理中,多变量GARCH模型有助于建立更准确的风险模型,以帮助投资者构建风险调整后的收益最大化的投资组合。
-
金融衍生品定价: 多变量GARCH模型用于衍生品定价和风险管理,例如期权、期货和其他金融衍生品的定价模型。
-
宏观经济研究: 在经济学中,多变量GARCH模型可用于分析多个宏观经济变量之间的条件异方差性,以深入了解宏观经济波动和政策决策。
-
时间序列分析: 多变量GARCH模型用于对多个时间序列数据进行建模,以分析它们之间的相互作用和动态关系。
优点如下:
-
考虑了波动性的动态性: 多变量GARCH模型考虑了条件异方差性的动态性,即波动性会根据历史信息的变化而变化。这更贴近实际市场情况,尤其是金融市场中的波动性通常是时间变化的。
-
处理多个变量之间的相关性: 该模型允许分析多个相关变量的条件异方差性,因此可以揭示它们之间的相互作用和影响,这对于风险管理和资产组合管理至关重要。
-
有丰富的变种: 多变量GARCH模型有多种变种,如BEKK-GARCH、DCC-GARCH等,可根据不同问题的需求进行调整和扩展,以适应复杂的建模情境。
-
有效的风险管理工具: 通过测量不同资产或变量之间的风险和相关性,多变量GARCH模型为风险管理提供了有效的工具,使投资者能够更好地管理投资组合风险。
下面开始多变量GARCH模型的R代码实战。
(1)数据准备
数据使用Brent原油数据和Wti原油数据,研究二者之间的条件异方差性。
dat1.tmp <-read.csv("E:/brent.csv")
head(dat1.tmp)输出结果:
dat2.tmp <- read.csv("E:/wti.csv")
head(dat2.tmp)输出结果:
Dates Open High Low Last Change Settle Volume Open.Interest
1 1983/3/30 29.01 29.56 29.01 NA NA 29.40 949 470
2 1983/3/31 29.40 29.60 29.25 NA NA 29.29 521 523
3 1983/4/4 29.30 29.70 29.29 NA NA 29.44 156 583
4 1983/4/5 29.50 29.80 29.50 NA NA 29.71 175 623
5 1983/4/6 29.90 29.92 29.65 NA NA 29.90 392 640
6 1983/4/7 29.90 30.20 29.86 NA NA 30.17 817 795
dat1=xts::as.xts(dat1.tmp[,5], as.Date(dat1.tmp[,1]))#将Brent原油数据中的第五列Settle与第一列时间合并
dat2=xts::as.xts(dat2.tmp[,7], as.Date(dat2.tmp[,1]))#与上面同理
head(dat1); head(dat2)输出结果:
[,1]
1990-08-17 27.12
1990-08-20 27.38
1990-08-21 27.63
1990-08-22 30.19
1990-08-23 30.85
1990-08-24 30.10
[,1]
1983-03-30 29.40
1983-03-31 29.29
1983-04-04 29.44
1983-04-05 29.71
1983-04-06 29.90
1983-04-07 30.17
Y1x=diff(log(dat1))*100; Y2x=diff(log(dat2))*100 #计算报酬率
Data=na.omit(merge(Y1x,Y2x))
colnames(Data)=c("Brent","Wti")
head(Data)输出结果:
Brent Wti
1990-08-20 0.9541357 -0.2447982
1990-08-21 0.9089319 -0.5265942
1990-08-22 8.8608605 9.4317719
1990-08-23 2.1626007 2.2487092
1990-08-24 -2.4611579 -3.2466251
1990-08-28 -12.0610951 3.5411621
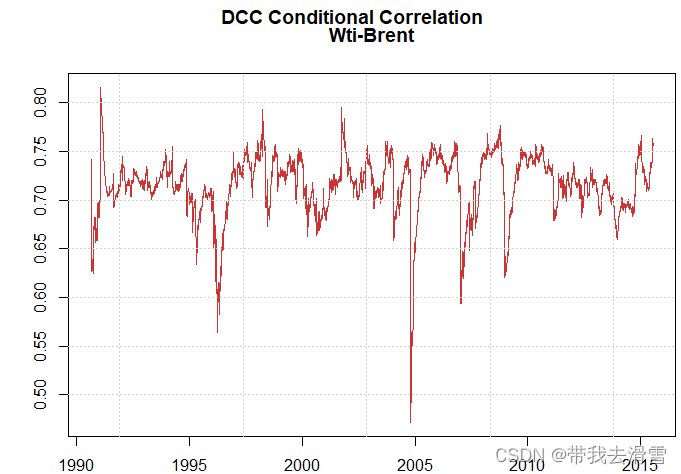
可以绘制 Brent和Wti的时间序列图,如下:
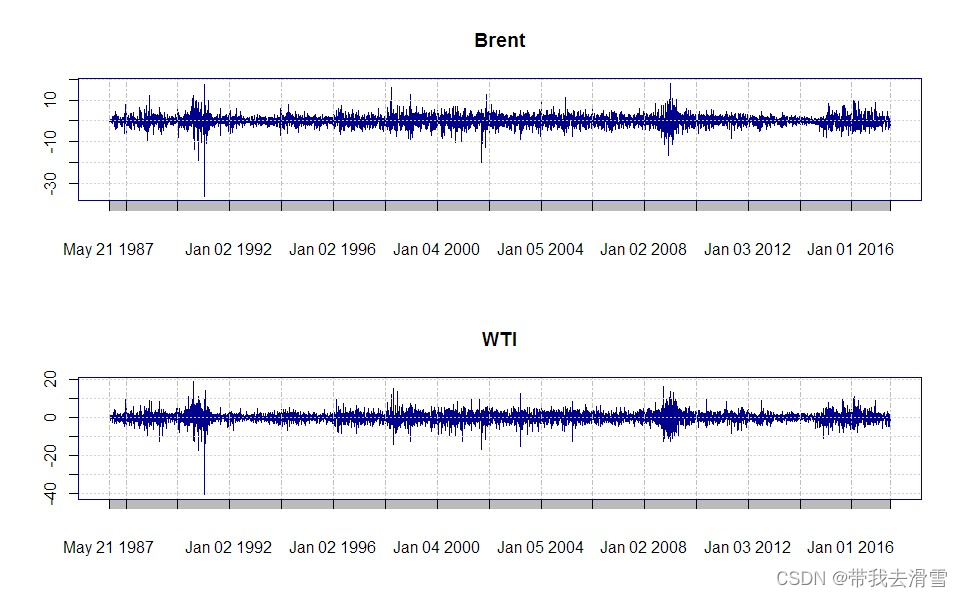
(2)估计基准DCC模型
library(rmgarch)
meanSpec=list(armaOrder=c(1,0), include.mean=TRUE, archpow=2)
varSpec=list(model="eGARCH", garchOrder = c(2,1))
distSpec = c("mvt")
spec = ugarchspec(mean.model=meanSpec, variance.model=varSpec)
mySpec0=multispec(list(spec, spec))
mySpec = dccspec(mySpec0, VAR = TRUE, robust = TRUE, lag.max =20, lag.criterion = "AIC", model="aDCC", distribution=distSpec)
fitDcc=dccfit(data=Data, mySpec, solver="solnp")
show(fitDcc)输出结果:
*---------------------------------*
* DCC GARCH Fit *
*---------------------------------*Distribution : mvt
Model : aDCC(1,1)
No. Parameters : 99
[VAR GARCH DCC UncQ] : [82+12+4+1]
No. Series : 2
No. Obs. : 6176
Log-Likelihood : -26580.6
Av.Log-Likelihood : -4.3Optimal Parameters
-----------------------------------
Estimate Std. Error t value Pr(>|t|)
[Brent].omega 0.014021 0.002192 6.39720 0.000000
[Brent].alpha1 -0.042463 0.029515 -1.43870 0.150235
[Brent].alpha2 0.034299 0.028255 1.21393 0.224775
[Brent].beta1 0.993653 0.000022 45405.17851 0.000000
[Brent].gamma1 0.145203 0.038973 3.72572 0.000195
[Brent].gamma2 -0.017929 0.037409 -0.47927 0.631746
[Wti].omega 5.035586 0.253793 19.84131 0.000000
[Wti].alpha1 0.627256 0.093282 6.72427 0.000000
[Wti].alpha2 0.242307 0.193114 1.25473 0.209576
[Wti].beta1 0.030845 0.034868 0.88462 0.376359
[Wti].gamma1 0.934502 0.134395 6.95337 0.000000
[Wti].gamma2 3.460364 0.222249 15.56975 0.000000
[Joint]dcca1 0.006693 0.003728 1.79531 0.072604
[Joint]dccb1 0.973724 0.009904 98.32013 0.000000
[Joint]dccg1 0.002541 0.003605 0.70495 0.480842
[Joint]mshape 4.000000 0.141729 28.22291 0.000000Information Criteria
---------------------
Akaike 8.6398
Bayes 8.7476
Shibata 8.6393
Hannan-Quinn 8.6772
Elapsed time : 1.39972
(3)取出对象和绘图
GARCH=sigma(fitDcc)
head(GARCH)输出结果:
Brent Wti
1990-08-20 2.221890 2.462386
1990-08-21 2.221890 2.462386
1990-08-22 2.165188 2.758191
1990-08-23 2.549332 45.850703
1990-08-24 2.616450 1370.848840
1990-08-28 2.742976 2.935267
dev.new(); plot(fitDcc,which=4)
dev.new(); nisurface(fitDcc)
COV=rcov(fitDcc)
COV
Rho=rcor(fitDcc)
Rho
COV12=as.data.frame(Cov[1,2,])
head(COV12)
Rho12=as.data.frame(Rho[1,2,])
head(Rho12)
DCCtest(Data, garchOrder = c(1,1), n.lags = 1, solver = "solnp", solver.control = list(), cluster = NULL, Z = NULL)输出结果:
(4)设置条件多样化
估计基准DCC模型中的代码使用了设定条件均一样的两笔数据。实际上 ,除了概率分布必须相同外,均值和方差的形式可以选择不一样的。
library(rmgarch)
meanSpec1<-list(armaOrder=c(1,0), include.mean=TRUE, archpow=2)
varSpec1<-list(model="eGARCH", garchOrder = c(2,1))
meanSpec2<-list(armaOrder=c(1,1), include.mean=TRUE, archpow=2)
varSpec2<-list(model="sGARCH", garchOrder = c(1,2))
distSpec<-c("mvt")
spec1<-ugarchspec(mean.model=meanSpec1, variance.model=varSpec1)
spec2<-ugarchspec(mean.model=meanSpec2, variance.model=varSpec2)
mySpec2<-multispec(list(spec1,spec2))
mySpecX<-dccspec(mySpec2, VAR = TRUE, robust = TRUE, lag.max =20 ,lag.criterion = "AIC", model="aDCC", distribution=distSpec)
fitDcc2<-dccfit(data=Data, mySpecX, solver="solnp")
show(fitDcc2)
slot(fitDcc2,"mfit")$matcoef
需要数据集的家人们可以去百度网盘(永久有效)获取:
链接:https://pan.baidu.com/s/1E59qYZuGhwlrx6gn4JJZTg?pwd=2138
提取码:2138
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!