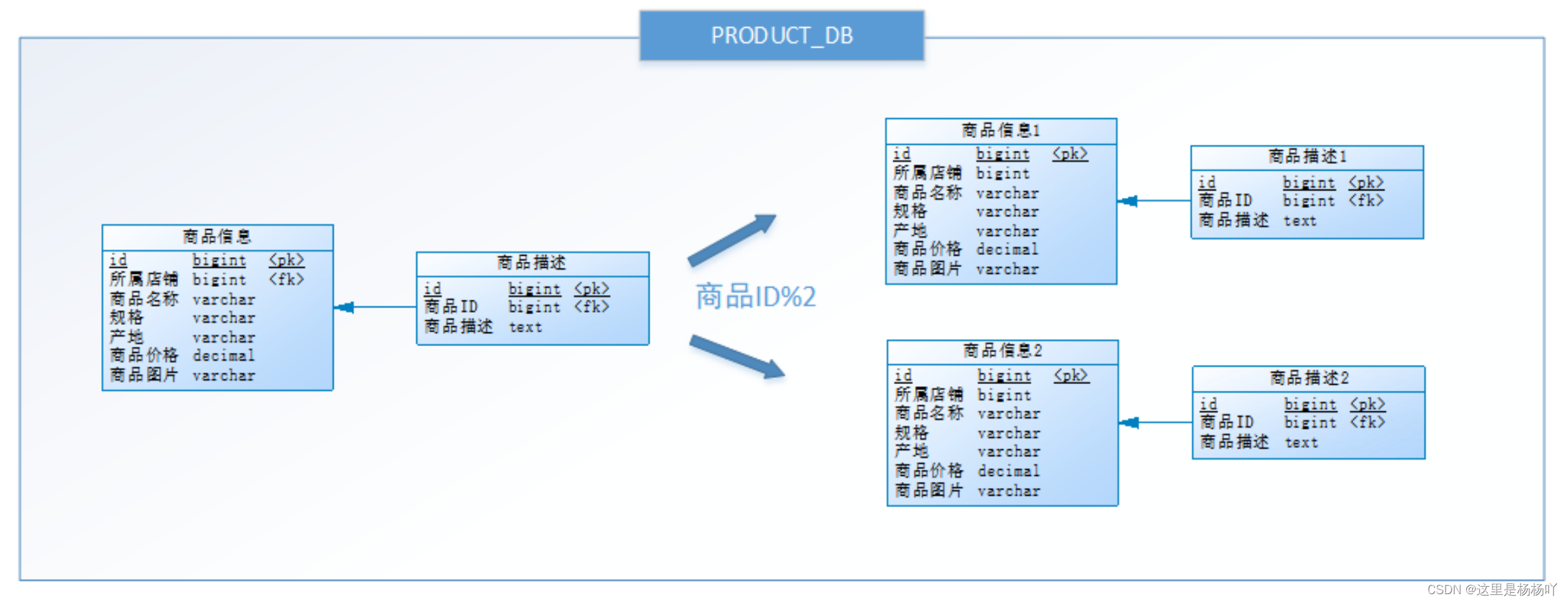
P1564 膜拜 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题意：

思路：

这是个经典模型：数列分段DP，在其他地方也出现过：(150条消息) 代码源每日一题div1 DP 数组划分_lamentropetion的博客-CSDN博客

这类DP模型核心是：

先去枚举阶段，这里的阶段是这样枚举的：

for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
        }
    }

不难看出，这样确实是保证了拓扑序，即保证了需要求的值在之前都求过了

在数组划分那道题也是这样划分阶段的

然后去枚举状态，在这里状态不需要枚举，因为在这道题中状态已经随着阶段的确定而确定了

然后去枚举决策，即枚举上一层的状态：

其实就是去枚举区间[j,i]的状态，当区间满足条件时再转移

当j确定时，状态也就确定了，这样就能从j转移过来了

对于这道题，我们设dp[i]表示选到第 i 个人需要的机房数

我们把膜拜甲记为1，膜拜乙记为-1，这样check区间就是满足区间和<=m或==i-j+1，check就是O(1)的复杂度

所以这里的小trick也可以总结一下：讨论两种东西之差时，可以编码成1和-1，这样会方便很多

Code：

#include <bits/stdc++.h>
using namespace std;
//#define int long long
const int mxn=3e3+10,mxv=4e2+10;
int n,m;
int dp[mxn],a[mxn],s[mxn];
void solve(){
    memset(dp,0x3f,sizeof(dp));
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++){
        if(a[i]==1) s[i]=s[i-1]+1;
        else s[i]=s[i-1]-1;
    }
    dp[0]=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            if((abs(s[i]-s[j-1])<=m)||(abs(s[i]-s[j-1])==i-j+1)) dp[i]=min(dp[i],dp[j-1]+1);
        }
    }
    cout<<dp[n]<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    while(__--)solve();return 0;
}