AtCoder Beginner Contest 325 题解 A-E

news2024/12/23 17:32:35

A - Takahashi san

原题链接

题目描述
给你两个字符串，将第二个字符串改为san后与第一个字符串一起输出

public static void solve() throws IOException {
    String s1 = readString(), s2 = readString();
    printWriter.println(s1 + " " + "san");
}

B - World Meeting

原题链接

题目描述
一个公司有 $N$ 个基地，第 $i$ 个基地有 $W_i$ 名员工，该基地所在区域的时间是 $X_i$ ，现在你是公司老总，想要在 $\sim 18:00$ 内开一个会议，要求让最多员工参会，求出这个员工数最多能是多少。

思路：模拟

枚举时间偏移量 $p$ ( $\sim 23$ )，再遍历 $N$ 个基地，求在 $p$ 的偏移量下能参会的最多员工。

public static void solve() throws IOException {
    int n = readInt();
    Pair[] pairs = new Pair[n + 1];
    for (int i = 1; i <= n; i++) {
        int a = readInt(), b = readInt();
        pairs[i] = new Pair(a, b);
    }
    long max = 0;
    for (int i = 0; i < 24; i++) {
        long cur = 0;
        for (int j = 1; j <= n; j++) {
            int t = (pairs[j].second + i) % 24;
            if (t >= 9 && t <= 17) cur += pairs[j].first;
        }
        max = Math.max(max, cur);
    }
    printWriter.println(max);
}

C - Sensors

原题链接

题目描述
有一个 $n$ 行 $m$ 列的二维网格，网格的部分点上有传感器，传感器会向自己相邻的 $8$ 个方向上的点传染，如果两个传感器相邻，那么他们发挥的作用等于一个传感器，求出最终发挥作用的传感器有多少个。

思路：深度优先搜索

遍历每一个未被遍历过的传感器，让其不断向自己相邻的传感器传染。

static char[][] map;
static boolean[][] vis;
static int n, m;

public static void solve() throws IOException {
    n = readInt(); m = readInt();
    map = utils.nextCharArray(n, m);
    vis=  new boolean[n + 1][m + 1];
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (!vis[i][j] && map[i][j] == '#') {
                cnt++;
                dfs(i, j);
            }
        }
    }
    printWriter.println(cnt);
}
// 偏移量，用于枚举8个方向
static int[] dx = new int[] {-1, -1, 0, 1, 1, 1, 0, -1}, dy = new int[] {0, 1, 1, 1, 0, -1, -1, -1};

public static void dfs(int a, int b) {
    for (int i = 0; i < 8; i++) {
        int nx = a + dx[i], ny = b + dy[i];
        if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && !vis[nx][ny] && map[nx][ny] == '#') {
            vis[nx][ny] = true;
            dfs(nx, ny);
        }
    }
}

D - Printing Machine

题目描述
有 $N$ 份产品在传送带上传送，传送带旁有一台打印机，第 $i$ 份产品将在 $T_i$ 秒内进入打印机的打印范围内，并在 $D_i$ 秒内离开打印机。现已知打印机一秒内最多只能打印一份产品，问打印机最多可以打印多少份产品。

思路：贪心+排序

首先对产品进入打印机打印范围的时间升序排序，方便多个打印机同时入队。
用一个优先队列(小顶堆)贪心地维护产品离开打印机的时间，让离开时间早的尽早打印。

public static void solve() throws IOException{
    int n = readInt();
    Pair[] pairs = new Pair[n + 1];
    for (int i = 1; i <= n; i++) {
        pairs[i] = new Pair(readLong(), readLong());
    }
    // 按进入打印机时间升序排序，方便入队
    Arrays.sort(pairs, 1, n + 1, (a, b) -> Long.compare(a.first, b.first));
    // 按离开打印机的时间升序排序
    PriorityQueue<Long> queue = new PriorityQueue<>();
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        queue.offer(pairs[i].first + pairs[i].second);
        // 进入打印机的时间相同，同时入队
        while (i + 1 <= n && pairs[i + 1].first == pairs[i].first) {
            queue.offer(pairs[i + 1].first + pairs[i + 1].second);
            i++;
        }
        long t = pairs[i].first;
        long bound = i + 1 <= n ? pairs[i + 1].first : Long.MAX_VALUE;
        // 在下一个产品来临之前打印
        while (queue.size() > 0 && t < bound) {
            long endTime = queue.poll();
            if (t <= endTime) {// 可以在对应时间离开打印机
                t++;
                cnt++;
            }
        }
    }
    printWriter.println(cnt);
}

E - Our clients, please wait a moment

题目描述
某国有 $N$ 座城市，你要从 $1$ 号城市到达 $N$ 号城市。现在有两种交通工具可供选择：公司汽车和火车。从城市 $i$ 到城市 $j$ 所需的时间如下：

乘公司汽车需 $D_{i,j} \times A$ 分钟
乘火车需 $D_{i,j} \times B + C$ 分钟

你可以从公司汽车换乘火车，但不能反之，而且你可以不花时间换乘。问从城市 $1$ 到城市 $N$ 最少需要多少分钟？

思路：分层图最短路+链式前向星存图

构造三条边，① $\to j$ ，距离为 $D_{i,j} \times A$ ② $\to (i + n)$ ，距离为 $0$ ③ $\to (j + n)$ ，距离为 $D_{i,j} \times B + C$
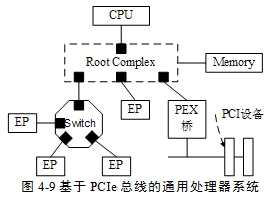
更复杂的分层图类似长下面这样，每两层之间至少有两个点相连

static int[] head;
static long[] d;
static Edge[] edges;
static int n, a, b, c;
static boolean[] st;

public static void solve() throws IOException{
    n = readInt(); a = readInt(); b = readInt(); c = readInt();
    head = new int[n * 2 + 10];
    edges = new Edge[(2 * n) * (2 * n) + 10];
    Arrays.setAll(edges, edge -> new Edge());
    d = new long[n * 2 + 10];
    Arrays.fill(d, Long.MAX_VALUE);
    st = new boolean[n * 2 + 10];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            int d = readInt();
            add(i, j, 1l * d * a);// 坐汽车
            add(i , i + n, 0l);// 两层之间建边，消费为0
            add(i + n, j + n, 1l * d * b + c);// 坐火车
        }
    }
    dijkstra();

    printWriter.println(Math.min(d[n], d[2 * n]));
}

public static void dijkstra() {
    PriorityQueue<long[]> queue = new PriorityQueue<>((a, b) -> Long.compare(a[1], b[1]));
    d[1] = 0;
    queue.offer(new long[] {1, 0});
    while (queue.size() > 0) {
        int t = (int) queue.poll()[0];
        if (st[t]) continue;
        st[t] = true;
        for (int i = head[t]; i != 0; i = edges[i].pe) {
            int to = edges[i].to;
            long w = edges[i].w;
            if (d[to] > d[t] + w) {
                d[to] = d[t] + w;
                queue.offer(new long[] {to, d[to]});
            }
        }
    }
}

public static void add(int a, int b, long c) {
    edges[idx] = new Edge(b, head[a], c);
    head[a] = idx++;
}