平衡二叉树(AVL)【java实现+图解】

一、平衡二叉树(AVL)

二、平衡二叉树的四种旋转

1.右旋转

2.左旋转

3. 左右旋转

4. 右左旋转

三、基于二叉搜索树之平衡二叉树的代码实现

1.具体方法思路

2.java代码实现

一、平衡二叉树(AVL)

一种自平衡二叉搜索树，它是在每个节点上增加一个平衡因子，然后通过调整树中节点的高度来保持树的平衡。平衡因子是左子树的高度减去右子树的高度，用它可以表示出当前节点的平衡程度。对于任意一个结点，左子树和右子树的高度差不能超过1，当一个节点的平衡因子绝对值大于1时，这个节点就被称为不平衡节点。

二、平衡二叉树的四种旋转

1.右旋转

    //左旋转
    public Node leftSpin(Node x){
        Node y = x.right;
        Node t2 = y.left;

        x.right = t2;
        y.left = x;
        //更新节点的高度
        x.height = Math.max(getHight(x.left),getHight(x.right))+1;
        y.height = Math.max(getHight(y.left),getHight(y.right))+1;
        return y;
    }

2.左旋转

    //右旋转
    public Node rightSpin(Node x){
        Node y = x.left;
        Node t2 = y.right;

        x.left = t2;
        y.right = x;
        //更新节点的高度
        x.height = Math.max(getHight(x.left),getHight(x.right))+1;
        y.height = Math.max(getHight(y.left),getHight(y.right))+1;
        return y;
    }

3. 左右旋转

先旋转成上面只需要右旋转的情况，再经过右旋转成平衡二叉树

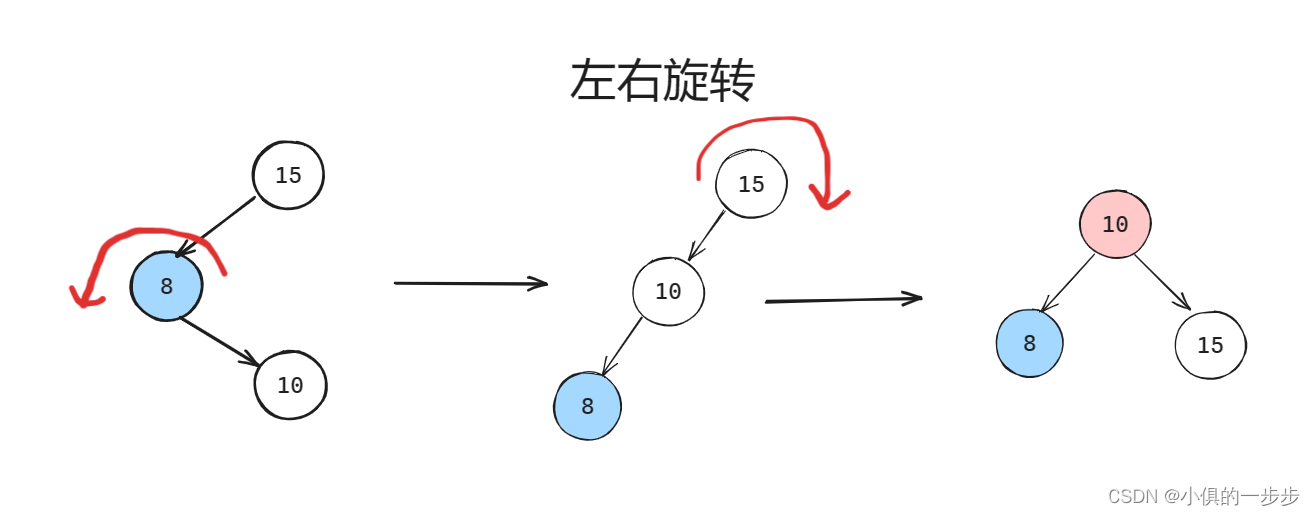
4. 右左旋转

先旋转成上面只需要左旋转的情况，再经过左旋转成平衡二叉树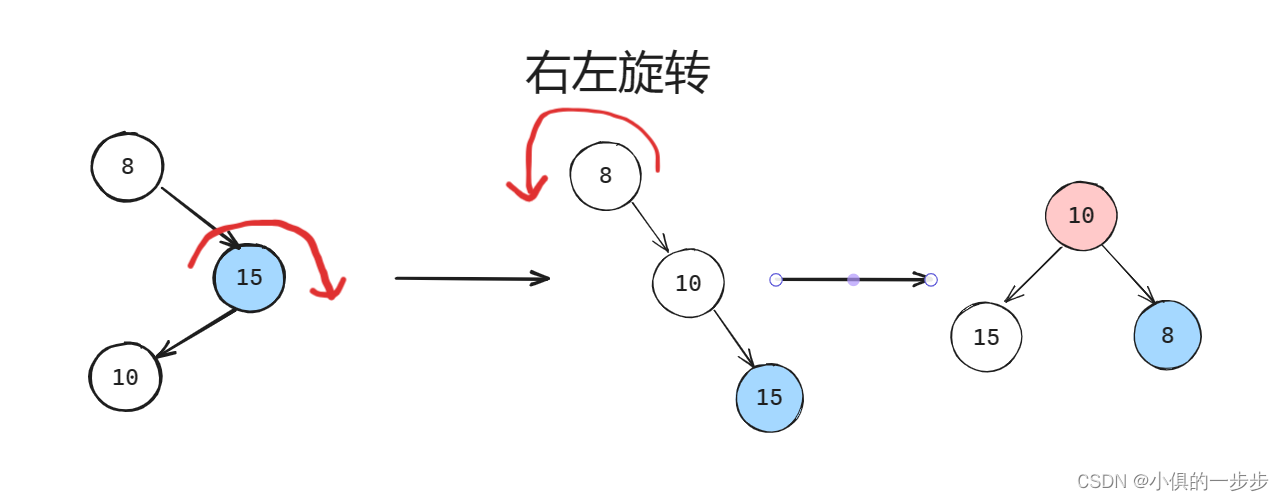

三、基于二叉搜索树之平衡二叉树的代码实现

1.具体方法思路

主要方法：

添加：每次添加一个节点后更新输的高度，平衡因子可能改变，依据平衡因子对二叉树进行调整；

删除：每删除一个节点后，也需要更新输的高度，平衡因子可能改变，依据平衡因子对二叉树进行调整。

辅助方法：

判断是否是二叉搜索树：通过中序遍历，将节点的前一个值与后一个值比较；

判断是否是平衡二叉树：通过判断每个子树的平衡因子的是否在[-1，1]区间内。

2.java代码实现

import java.util.*;
import java.util.stream.Collectors;

public class AVL<T extends Comparable<T>> {

    public class Node {
        T val;
        Node left;
        Node right;
        //以该节点为根的树的高度
        int height;

        //统计单词出现的次数
        int count;

        public Node(T val) {
            this.val = val;
            this.height = 1;//默认高度为1
            this.count = 1;
        }

        @Override
        public String toString() {
            return String.format("val:%s,heiget:%d,count:%d",this.val,this.height,this.count);
        }
    }

    private Node root;
    private Integer size;

    public AVL() {
        this.root = null;
        this.size = 0;
    }

    public boolean isEmpt() {
        return this.size == 0;
    }

    public Integer getSize() {
        return this.size;
    }


    //验证是否是二叉搜索树
    public  boolean isBinaryTree(){
        List<T> list = new ArrayList<>();
        midTraversal(list,this.root);
        for (int i = 1; i < list.size(); i++) {
            if (list.get(i-1).compareTo(list.get(i))>0){
                return false;
            }
        }
        return true;
    }

    //获取当前节点的高度
    public int getHight(Node node){
        if (node==null){
            return 0;
        }
        return node.height;
    }
    //获取当前节点的平衡因子
    public int getBalanceFactor(Node node){
        if (node==null){
            return 0;
        }
        return getHight(node.left)-getHight(node.right);
    }
    

    public boolean isBalanceTree(){
        return isBalanceTree(this.root);
    }

    //判断以node为节点的树是否是平衡二叉树
    private boolean  isBalanceTree(Node node){
        if (node==null){
            return true;
        }
        int balanceFactor = Math.abs(getBalanceFactor(node));

        if (balanceFactor>1){
            return false;
        }else {
            return isBalanceTree(node.left)&&isBalanceTree(node.right);
        }
    }
    
    //左旋转
    public Node leftSpin(Node x){
        Node y = x.right;
        Node t2 = y.left;

        x.right = t2;
        y.left = x;
        //更新节点的高度
        x.height = Math.max(getHight(x.left),getHight(x.right))+1;
        y.height = Math.max(getHight(y.left),getHight(y.right))+1;
        return y;
    }
    //右旋转
    public Node rightSpin(Node x){
        Node y = x.left;
        Node t2 = y.right;

        x.left = t2;
        y.right = x;
        //更新节点的高度
        x.height = Math.max(getHight(x.left),getHight(x.right))+1;
        y.height = Math.max(getHight(y.left),getHight(y.right))+1;
        return y;
    }

    //添加
    public void add(T val) {
        this.root = add(this.root, val);
    }

    private Node add(Node node, T val) {
        if (node == null) {
            this.size++;
            Node leafNode = new Node(val);
            return leafNode;
        }
        //当前节点的值小于添加的val,因此val做右孩子
        if (node.val.compareTo(val) < 0) {
            node.right = add(node.right, val);
            //更新高度
            node.height = Math.max(getHight(node.left),getHight(node.right))+1;
        } else if (node.val.compareTo(val) > 0){
            node.left = add(node.left, val);
            //更新高度
            node.height = Math.max(getHight(node.left),getHight(node.right))+1;
        }else {
            node.count++;
        }

        //添加后还要判断是否是平衡二叉树
        Node resNode = node;
        int balanceFactor = getBalanceFactor(node);
        if (balanceFactor>1&&getBalanceFactor(node.left)>=0){
            //右
            resNode = rightSpin(node);
        }else if (balanceFactor>1&&getBalanceFactor(node.left)<0){
            //左右
            node.left = leftSpin(node.left);
            resNode = rightSpin(node);
        }else if (balanceFactor<-1&&getBalanceFactor(node.right)<=0){
            //左
            resNode = leftSpin(node);
        }else if (balanceFactor<-1&&getBalanceFactor(node.right)>0){
            //右左
            node.right = rightSpin(node.right);
            resNode = leftSpin(node);
        }
        return resNode;
    }


    //删除操作
    //删除树中的val
    public void remove(T val){
        if (!contain(val)){
            return;
        }
        this.root = remove(this.root,val);
    }

    /**
     * 删除val
     * @param node
     * @param val
     * @return
     */
    public Node remove(Node node, T val){
        //    递归终止条件
        if (node == null) {
            return null;
        }
        Node resNode = null;
        if (node.val.compareTo(val) == 0) {
            this.size--;
            if (node.right==null){
                //右子树为空
                resNode = node.left;
            }else if (node.left==null){
                //左子树为空
                resNode = node.right;
            }else {
                //    左右子树都不为空
                //    1.找到删除节点的后继
                 Node suffixNode = getMinDG(node.right);
                // 2.删除后继
                suffixNode.right = remove(node.right,getMinDG(node.right).val);
                // 3.连接
                suffixNode.left = node.left;
                this.size++;
                //    返回删除后的根
                resNode = suffixNode;
            }
        }else if (node.val.compareTo(val)<0){
            node.right = remove(node.right,val);
            resNode = node;
        }else {
            node.left = remove(node.left,val);
            resNode =  node;
        }

        //删除节点可能为叶子结点
        if (resNode==null){
            return null;
        }
        //更新高度
        resNode.height = Math.max(getHight(resNode.left),getHight(resNode.right))+1;
        int balanceFactor = getBalanceFactor(resNode);
        if (balanceFactor>1&&getBalanceFactor(resNode.left)>=0){
            //右
            resNode = rightSpin(resNode);
        }else if (balanceFactor>1&&getBalanceFactor(resNode.left)<0){
            //左右
            resNode.left = leftSpin(resNode.left);
            resNode = rightSpin(resNode);
        }else if (balanceFactor<-1&&getBalanceFactor(resNode.right)<=0){
            //左
            resNode = leftSpin(resNode);
        }else if (balanceFactor<-1&&getBalanceFactor(resNode.right)>0){
            //右左
            resNode.right = rightSpin(resNode.right);
            resNode = leftSpin(resNode);
        }
        return resNode;
    }

    private Node getMinDG(Node node) {
        // 递归终止条件
        if (node.left == null) {
            return node;
        }
        //   递归操作
        return getMinDG(node.left);
    }

    public String midTraversal() {
        List<T> res = new ArrayList<>();
        midTraversal(res, this.root);
        return res.stream().map(item -> item.toString()).collect(Collectors.joining(","));
    }

    /**
     * 中序遍历
     *
     * @param result
     * @param node   当前节点
     * @return
     */
    private void midTraversal(List<T> result, Node node) {
        if (node == null) {
            return;
        }
        midTraversal(result, node.left);
        result.add(node.val);
        midTraversal(result, node.right);
    }

    public void showTree(){
        showTree(this.root);
    }
    private void showTree(Node node){
        if (node == null) {
            return;
        }
        showTree(node.left);
        System.out.print(node);
        System.out.println("BalanceFactor:"+getBalanceFactor(node));
        showTree(node.right);
    }

    //查询是否存在val
    public boolean contain(T val){
        return contain(this.root,val);
    }
    private boolean contain(Node node,T val){
    //    递归的终止条件
    //    查询到低也没有找到
        if (node==null){
            return false;
        }
    //    递归操作
        if (node.val.compareTo(val)==0){
            return true;
        }else if (node.val.compareTo(val)<0){
            return contain(node.right,val);
        }else {
            return  contain(node.left,val);
        }
    }
    //测试
    public static void main(String[] args) {
        AVL<String> bst = new AVL<>();

        List<String> list = ReadBookUtil.readBook("pride-and-prejudice.txt");
        list.stream().forEach(item->{
            bst.add(item);
        });
        System.out.println("是否是二分搜索树"+bst.isBinaryTree());
        System.out.println("是否是平衡二叉树"+bst.isBalanceTree());
        bst.showTree();
  
    }
}