实用数据结构【并查集】 - 原理
[一个问题]
若某个部落过于庞大,则部落成员见面也有可能不认识。
已知某个部落的成员关系图,任意给出其中两个人,判断是否有亲戚关系。规定:①若x、y 是亲戚,y 和z 是亲戚,则x 和z 也是亲戚;②若x、y是亲戚,则x 的亲戚也是y 的亲戚,y 的亲戚也是x 的亲戚。
如何才能快速判断两个人是否有亲戚关系呢?
以上规定中的第①条是传递关系,第②条相当于两个集合的合并,因此对该问题可以采用并查集轻松解决。
并查集是一种树形数据结构,用于处理集合的合并查询问题。
【算法步骤】
① 初始化。
将每个节点所在的集合号都初始化为其自身编号。
② 查找。
查找两个元素所在的集合,即找祖宗。查找时,采用递归的方法找其祖宗,找到祖宗(集合号等于自身)时停止;然后回归,回归时将祖宗到当前节点路径上的所有节点都统一为祖宗的集合号。
③ 若两个节点的集合号不同,则将两个节点合并为一个集合,合并时只需将一个节点的祖宗集合号修改为另一个节点的祖宗集合号。擒贼先擒王,只改祖宗即可!
【举个栗子】
假设现在有7个人,首先输入亲戚关系图,然后判断两个人是否有亲戚关系。
① 初始化
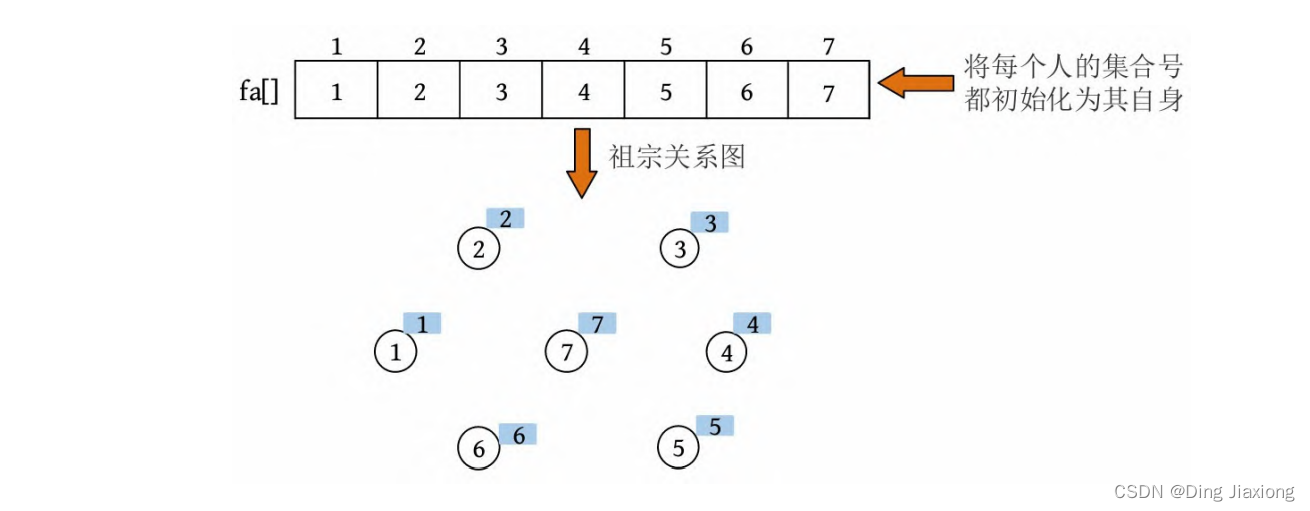
② 查找。
输入亲戚关系2、7,查找到2的集合号为2,7的集合号为7。
③ 合并。
两个元素的集合号不同,将两个元素合并为一个集合。在此约定将小的集合号赋值给大的集合号, 因此修改fa[7]=2。
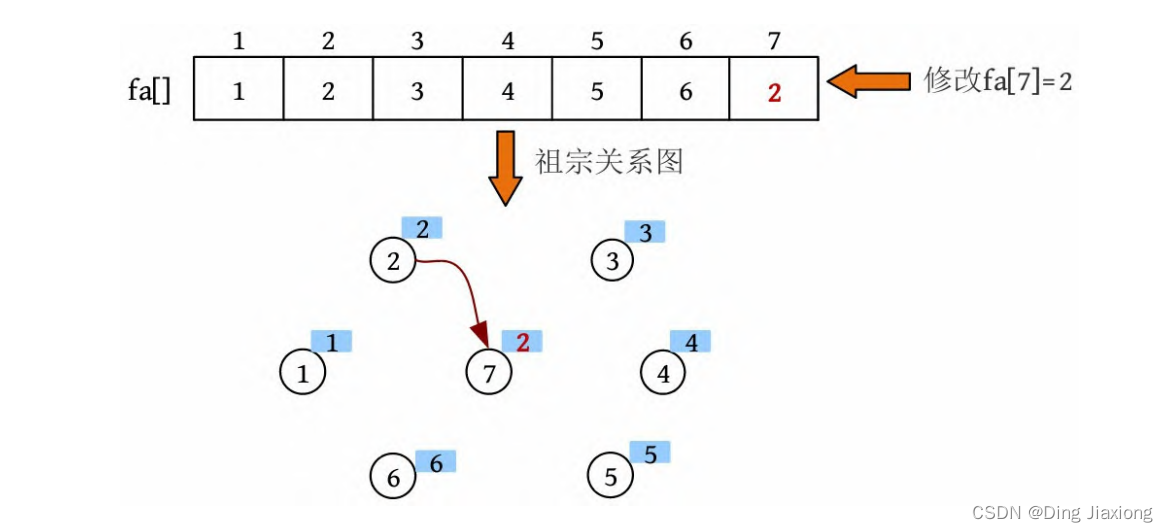
④ 查找。
输入亲戚关系4、5,查找到4的集合号为4,5的集合号为5。
⑤ 合并。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[5]=4。

⑥ 查找。输入亲戚关系3、7,查找到3的集合号为3,7的集合号为2。
⑦ 合并。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[3]=2。
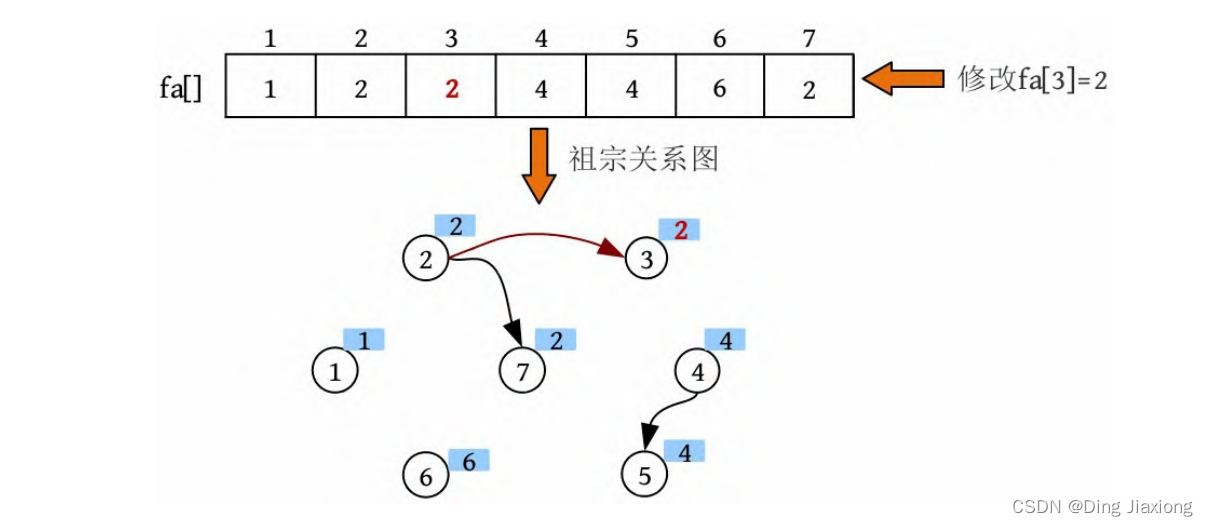
⑧ 查找。输入亲戚关系4、7,查找到4的集合号为4,7的集合号为2。
⑨ 合并。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[4]=2。
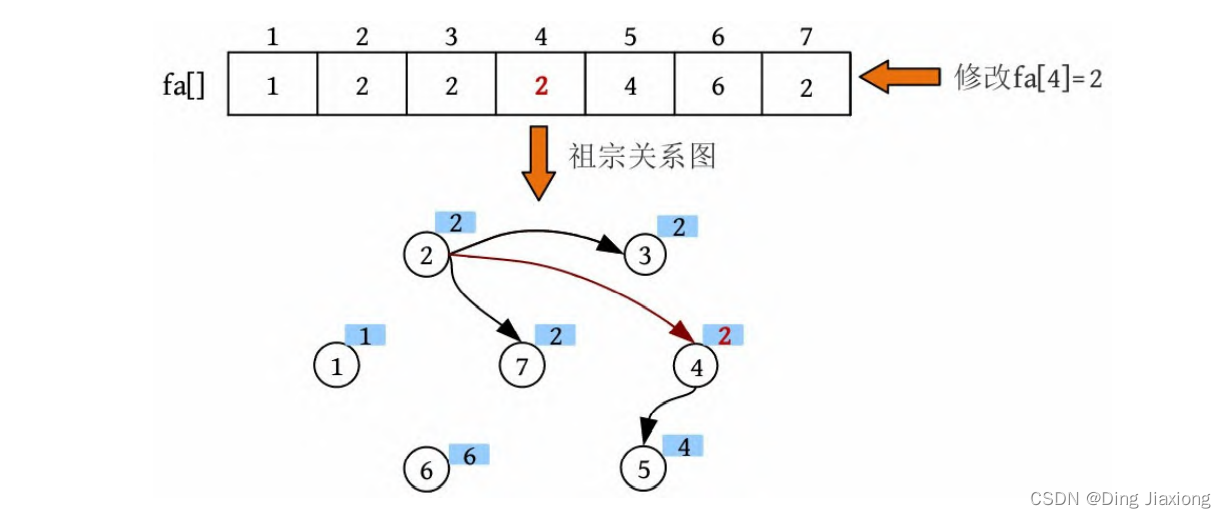
擒贼先擒王,只改祖宗即可!有两个节点的集合号为4,只需修改两个节点中的祖宗,无须将集合号为4的所有节点都检索一遍,这正是并查集的巧妙之处!
⑩ 查找。输入亲戚关系3、4,查找到3的集合号为2,4的集合号为2。
⑪ 合并。两个元素的集合号相同,无须合并。
⑫ 查找。输入亲戚关系5、7,查找到7的集合号为2,查找到5的集合号不等于5,所以找5的祖宗。首先找到其父节点4,4的父节点为2,2的集合号等于2(祖宗),搜索停止。返回时,将祖宗到当前节点路径上所有节点的集合号都统一为祖宗的集合号。更新5的集合号为祖宗的集合号2。
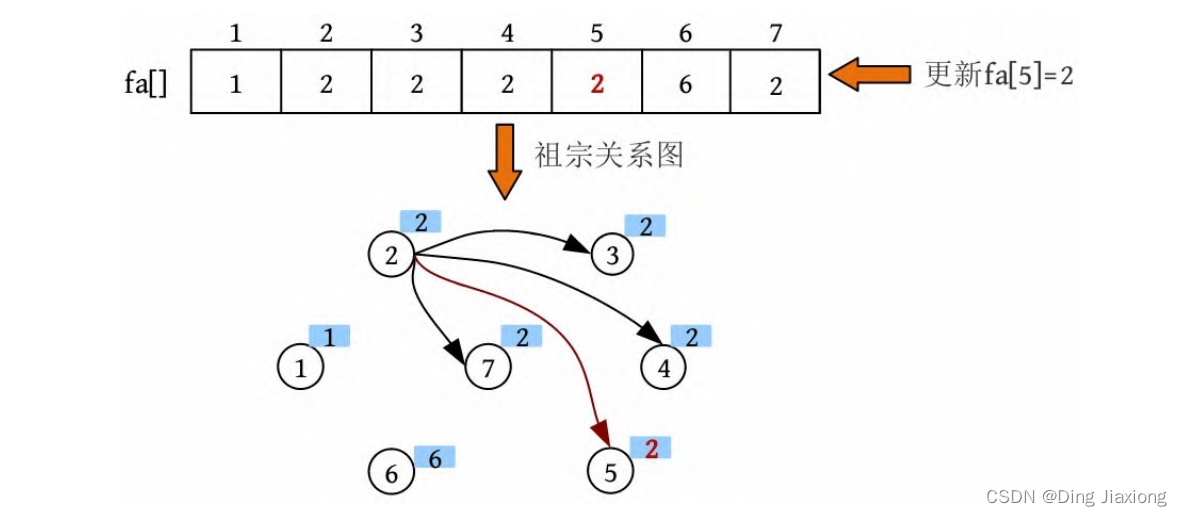
⑬ 合并。两个元素的集合号相同,无须合并。
⑭ 查找。输入亲戚关系5、6,查找到5的集合号为2,6的集合号为6。
⑮ 合并。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[6]=2。
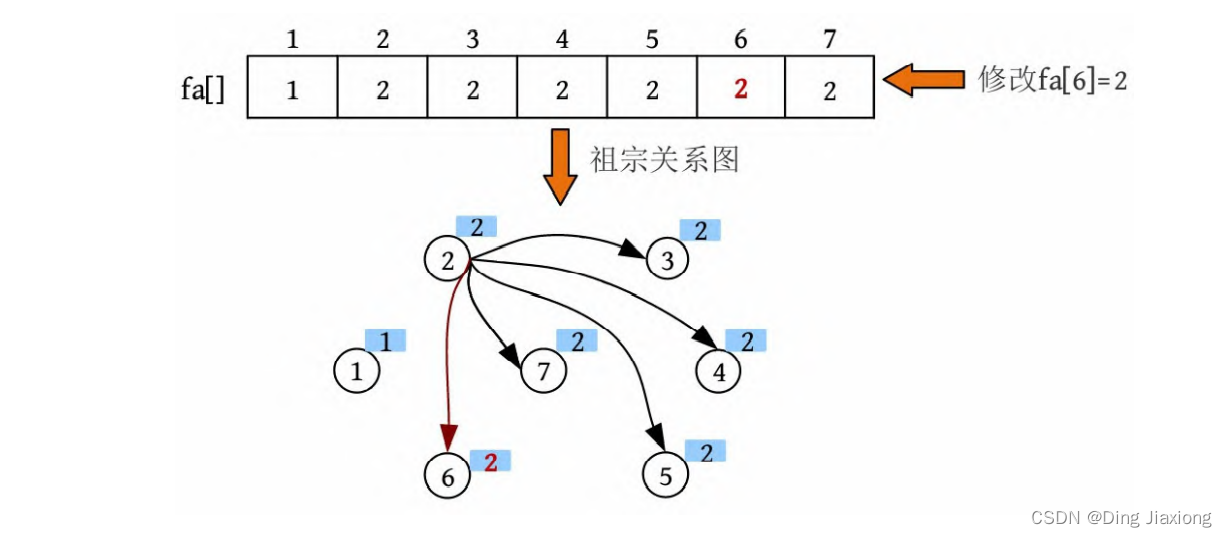
⑯ 查找。输入亲戚关系2、3,查找到2的集合号为2,3的集合号为2。
⑰ 合并。两个元素的集合号相同,无须合并。
⑱ 查找。输入亲戚关系1、2,查找到1的集合号为1,2的集合号为2。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[2]=1。
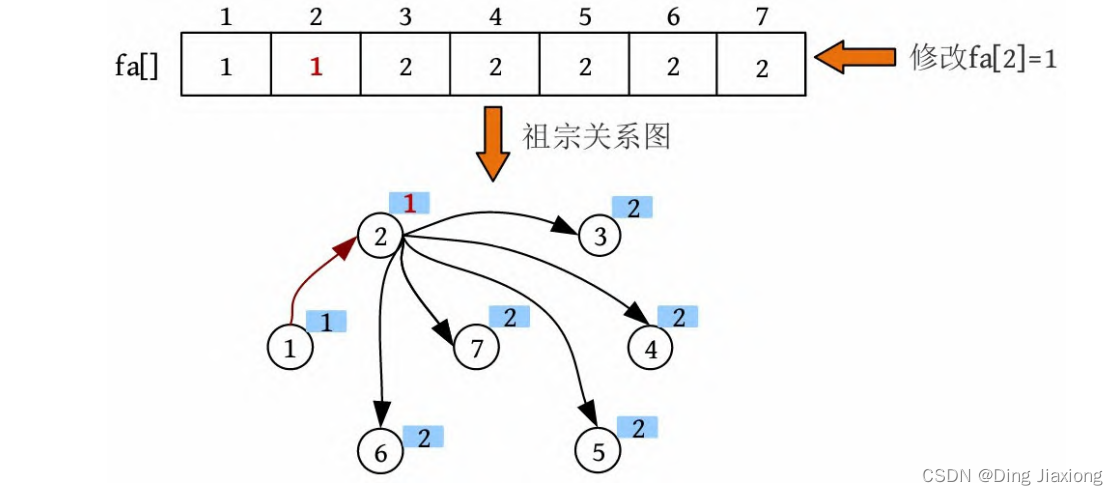
OK。假设到此为止,亲戚关系图已经输入完毕。可以看到3、4、5、6、7这些节点的集合号并没有被修改为1,这样做真的可以吗?
现在,判断5和2是不是亲戚关系,则过程如下。
① 查找到5的集合号为2,5的集合号不等于5,找其祖宗。首先查找到5的父节点2,2的父节点1,1的集合号为1(祖宗),搜索停止。将祖宗1到5这条路径上所有节点的集合号都更新为1。
② 查找到2的集合号为1,找其祖宗。2的祖宗为1,1的集合号为1(祖宗),搜索停止。将祖宗1到2这条路径上所有节点的集合号都更新为1。
③ 5和2的集合号都为1,因此5和2是亲戚关系。
【算法实现】
① 初始化。将节点i 的集合号初始化为其自身编号。
void init(){ //初始化集合号
for(int i = 1; i <= n ; i ++){
fa[i] = i; //把节点i 的集合号初始化为其 自身编号
}
}
② 查找。查找两个元素所在的集合,即找祖宗。查找时,采用递归的方法找其祖宗(集合号等于自身)。回归时,将祖宗到当前节点路径上的所有节点都统一为祖宗的集合号。
void Find(int x){ //查找
if(x != fa[x]){
fa[x] = Find(fa[x]);
}
return fa[x];
}
fa[x ]表示x 的集合号,若x !=fa[x ],则说明x 节点不是祖宗。继续向上找,找到祖宗后返回。回归时将祖宗到当前节点路径上的所有节点都统一为祖宗的集合号,如下图所示。
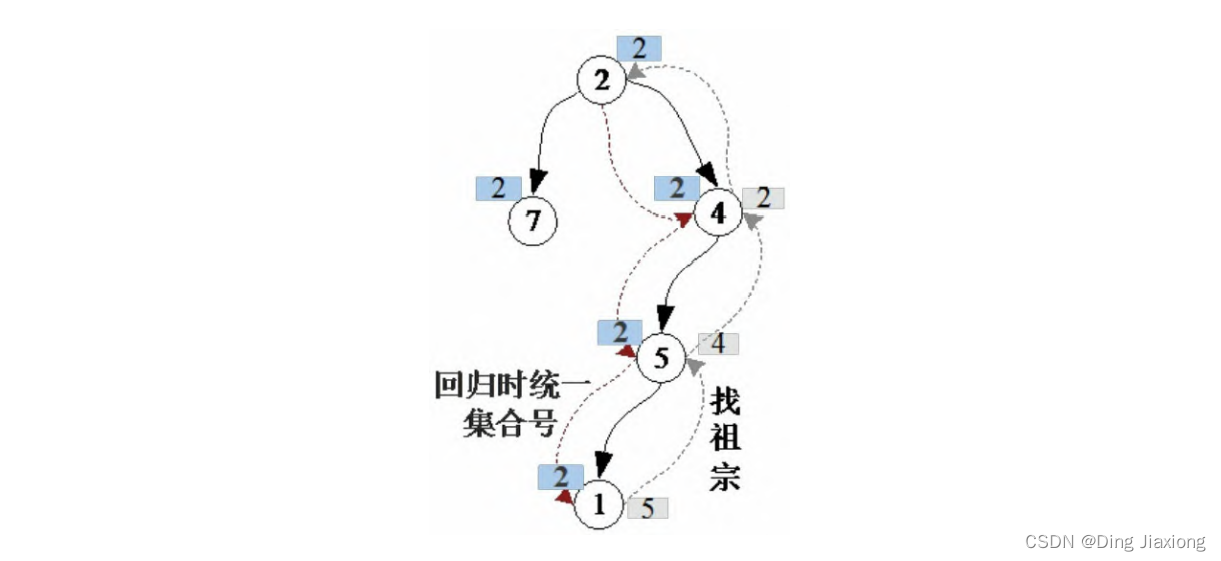
③ 合并。先找到x 的集合号a ,y 的集合号b ,若a 和b 相等,则无须合并。若a 和b 不相等,则将a 的集合号修改为b ,或者将b 的集合号修改为a 。擒贼先擒王,只改祖宗即可
void Union(int x, int y){ //合并
int a = Find(x);
int b = Find(y);
if(a != b){
fa[b] = a;
}
}
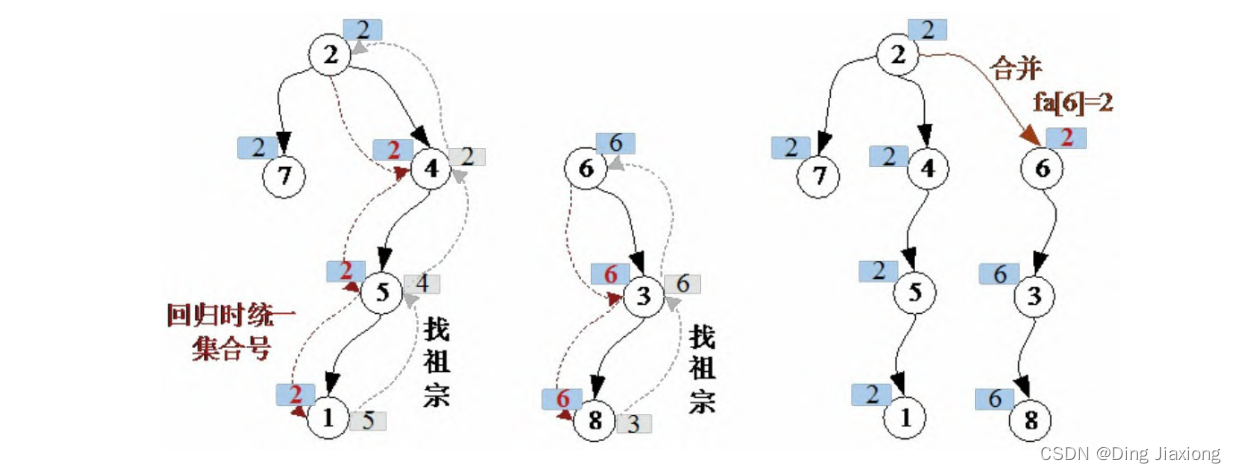
输入1和8的亲戚关系,先找到1的祖宗2,8的祖宗6,将6的集合号修改为2即可。
【算法分析】
若有n 个节点、e 条边(关系),则每条边(u , v )进行集合合并时,都要查找u 和v 的祖宗,查找的路径为从当前节点一直到根节点,n 个节点组成的树的平均高度为logn ,因此并查集中,合并集合的时间复杂度为O (e logn )。