第五章:双指针、离散化、二进制运算与区间合并
- 一、双指针
- 1、什么是双指针?
- 2、双指针的模板
- 3、双指针例题
- (1)思路:
- (2)解答:
- C++版:
- C版:
- 二、离散化
- 1、什么是离散化?
- 2、离散化映射
- 3、模板
- (1)C++
- (2)C
一、双指针
1、什么是双指针?
双指针运算常用在数组中,其实就是创建两个下标通过一定的规律去访问数组。基本上,两个指针最多都只会遍历数组一次,那么利用双指针算法的时间复杂度就是O(N)。除此之外,利用双指针算法的题目,大部分可以套双层循环去遍历,那么这种暴力方式的时间复杂度就是O(N^2^)。
因此双指针算法可以大大地降低时间复杂度。
2、双指针的模板
C++和C的模板是一致的。
int j=0;
for(int i=0;i<n;i++)
{
while(j<n&&check(j))j++;
}
这个模板中的重点是check函数的思考。
3、双指针例题
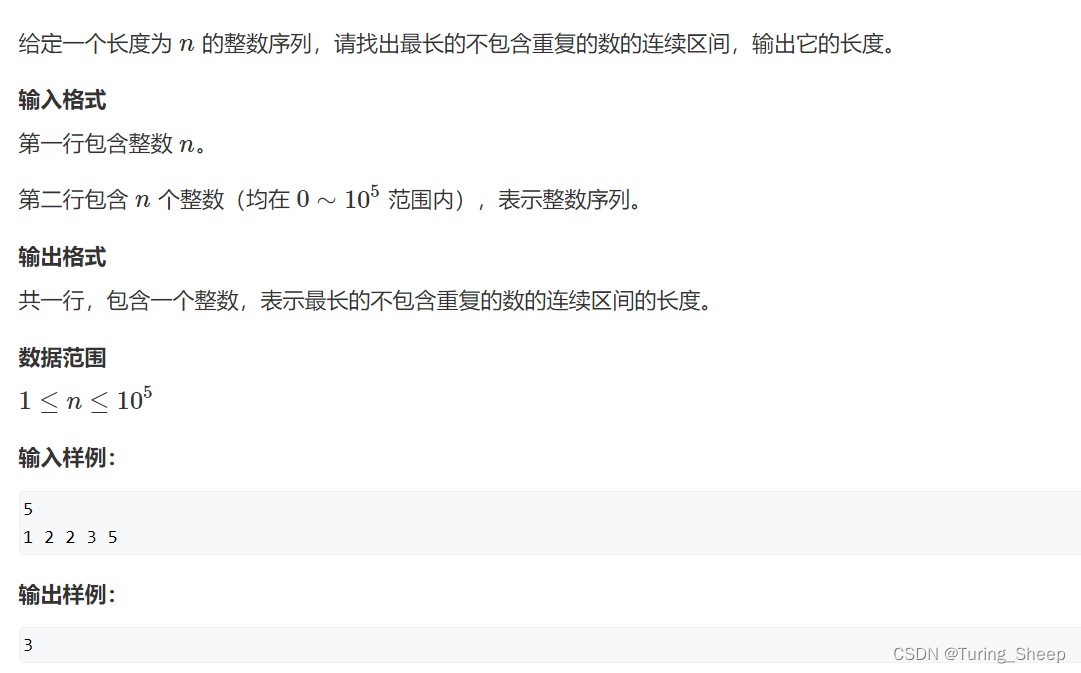
(1)思路:
我们创建两个指针,让j,i分别指向一段序列的两端,然后去判断这一段是否有重复的数字。倘若没有重复的元素,我们会记录此时的长度。
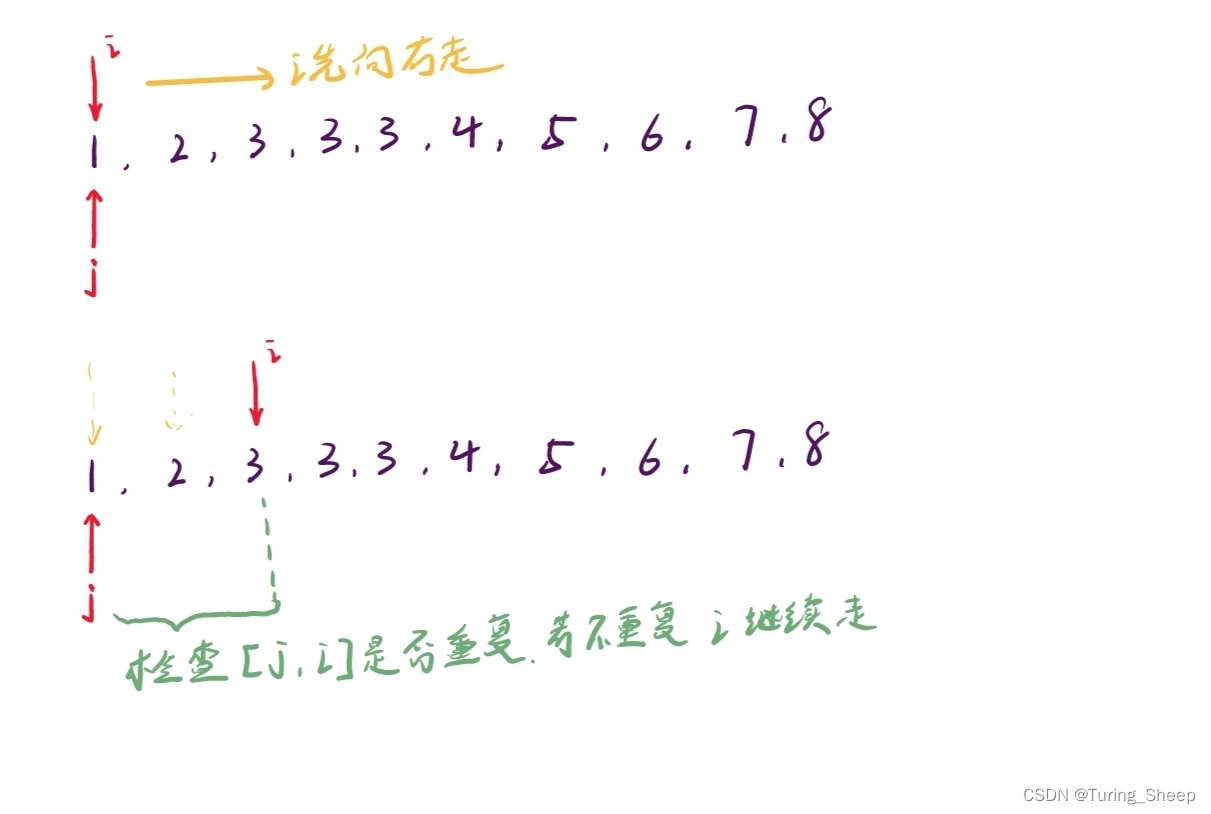
那么我们假设遇到重复,我们又该如何修正呢?
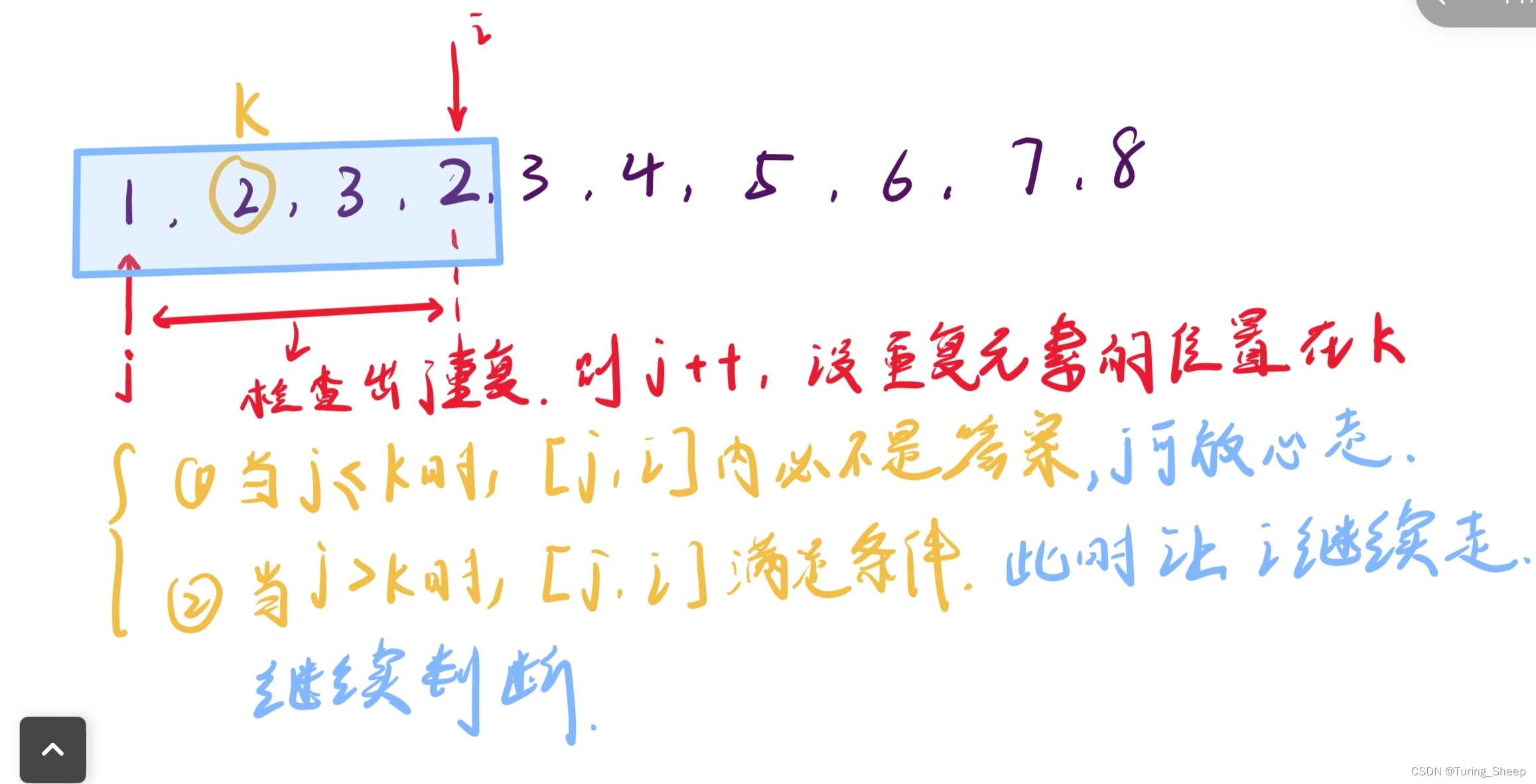
我们先明白以下的逻辑:
序列出现重复,一定是因为i所指的数组元素与序列中的某个元素重复了。
此时我们让j去寻找这个重复元素,在找到之前,此时i,j所包含的序列一定不是答案, 因此我们可以放心的移动。
当我们找到重复元素后,我们让j指向它的下一个元素,此时就排除了这个重复元素,那么此时的i,j区间的序列,满足了不重复的条件,那么此时我们继续让i去移动。
由上述操作:
我们就能够总结出i和j的作用:
(1)i是为了尽可能地寻找最长的序列。
(2)j是为了找到重复的序列。
那么我们的check函数如何写呢?
如下图所示:
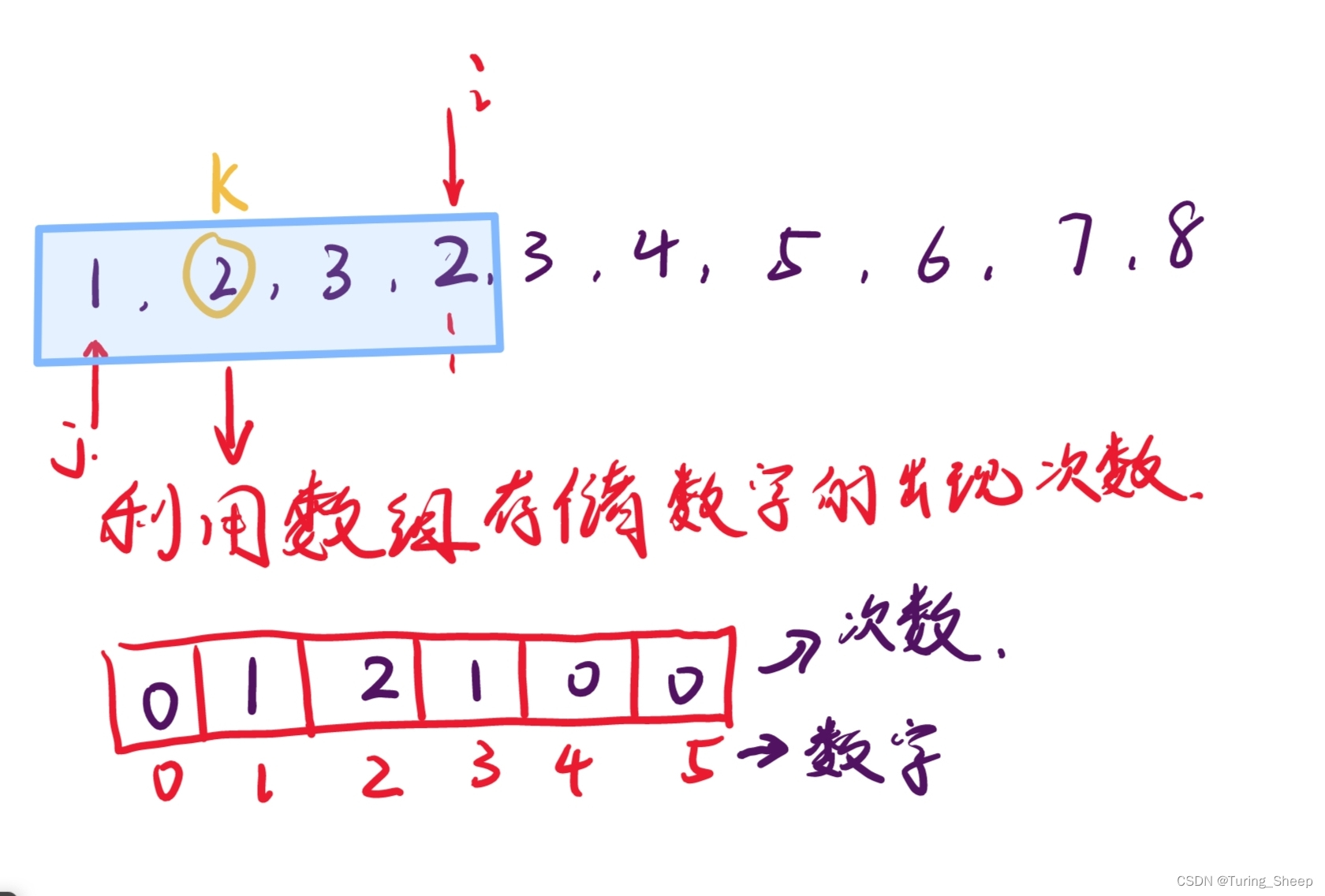
因为一个序列是在变化的,那么我们如何维护一个动态的判断数组?
如下图所示:

(2)解答:
C++版:
#include<iostream>
using namespace std;
const int N=100010;
int arr[N];
int S[N];
int main()
{
int n,res=0,j=0;
cin>>n;
for(int i=0;i<n;i++)scanf("%d",arr+i);
for(int i=0;i<n;i++)
{
S[arr[i]]++;
while(S[arr[i]]>1)
{
S[arr[j]]--;
j++;
}
res=max(res,i-j+1);
}
cout<<res<<endl;
return 0;
}
C版:
#include<stdio.h>
int arr[100010];
int S[100010];
int max(int a,int b)
{
return a>b?a:b;
}
int main()
{
int n;
int res=0,j=0;
scanf("%d",&n);
for(int i=0;i<n;i++)scanf("%d",arr+i);
for(int i=0;i<n;i++)
{
S[arr[i]]++;
while(S[arr[i]]>1)
{
S[arr[j]]--;
j++;
}
res=max(res,i-j+1);
}
printf("%d",res);
return 0;
}
二、离散化
1、什么是离散化?
假设一个数组的长度是10,但是每个元素的数据范围是1-100,那么假设这个数组是:
1,44,77,34,23,45,56,12,2,100。
这个例子就是一个离散化的,他的数据的元素范围是大于这个数组长度范围的。我们可以用下面的图片进一步体会什么是离散化。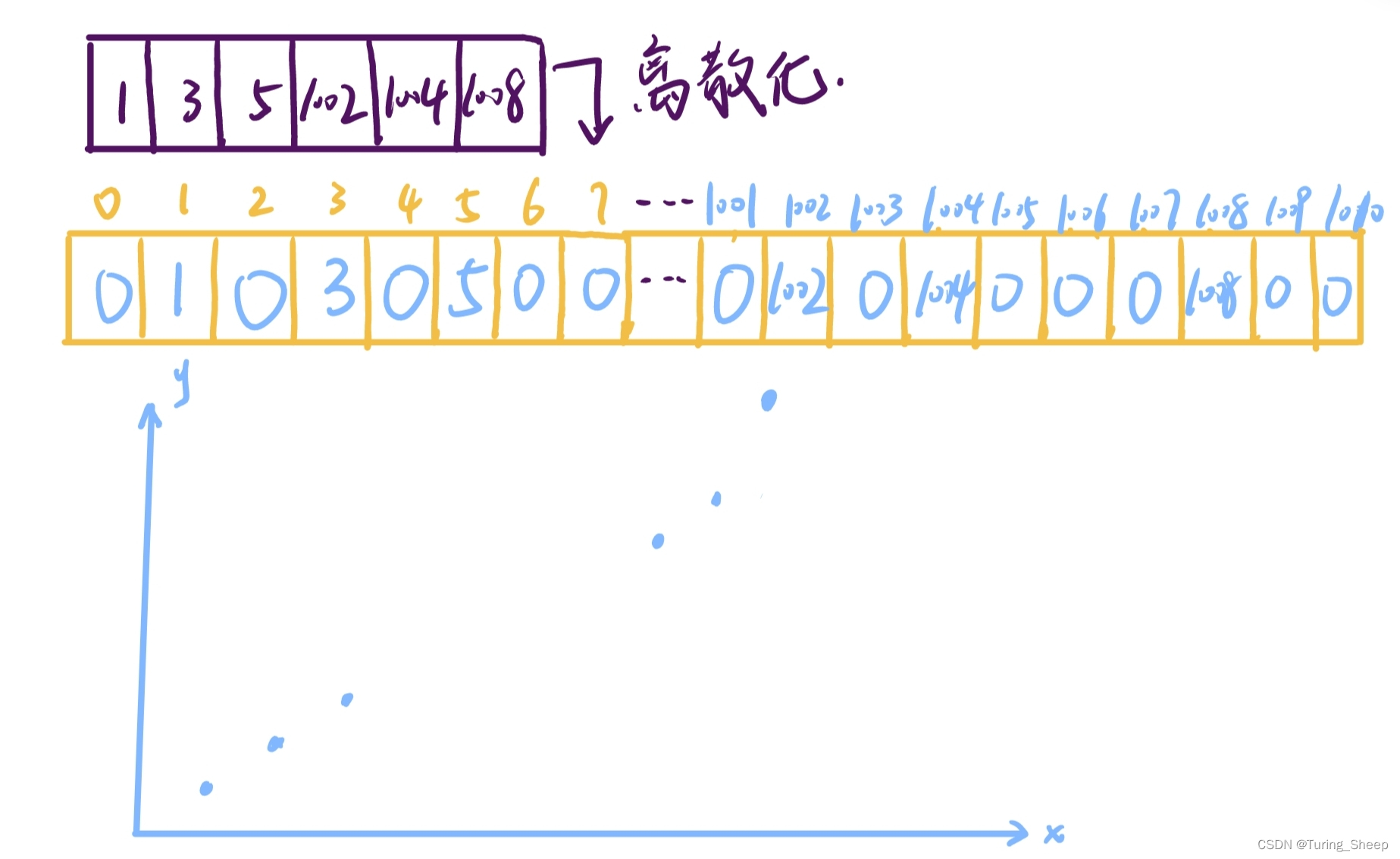
上图所示,我们将6个元素之间数值差距很大的数组,放到黄色数组中,黄色数组的特点就是元素的下表和元素内容是一致的,这种情况下,我们的黄框数组就浪费了非常大的空间。
2、离散化映射
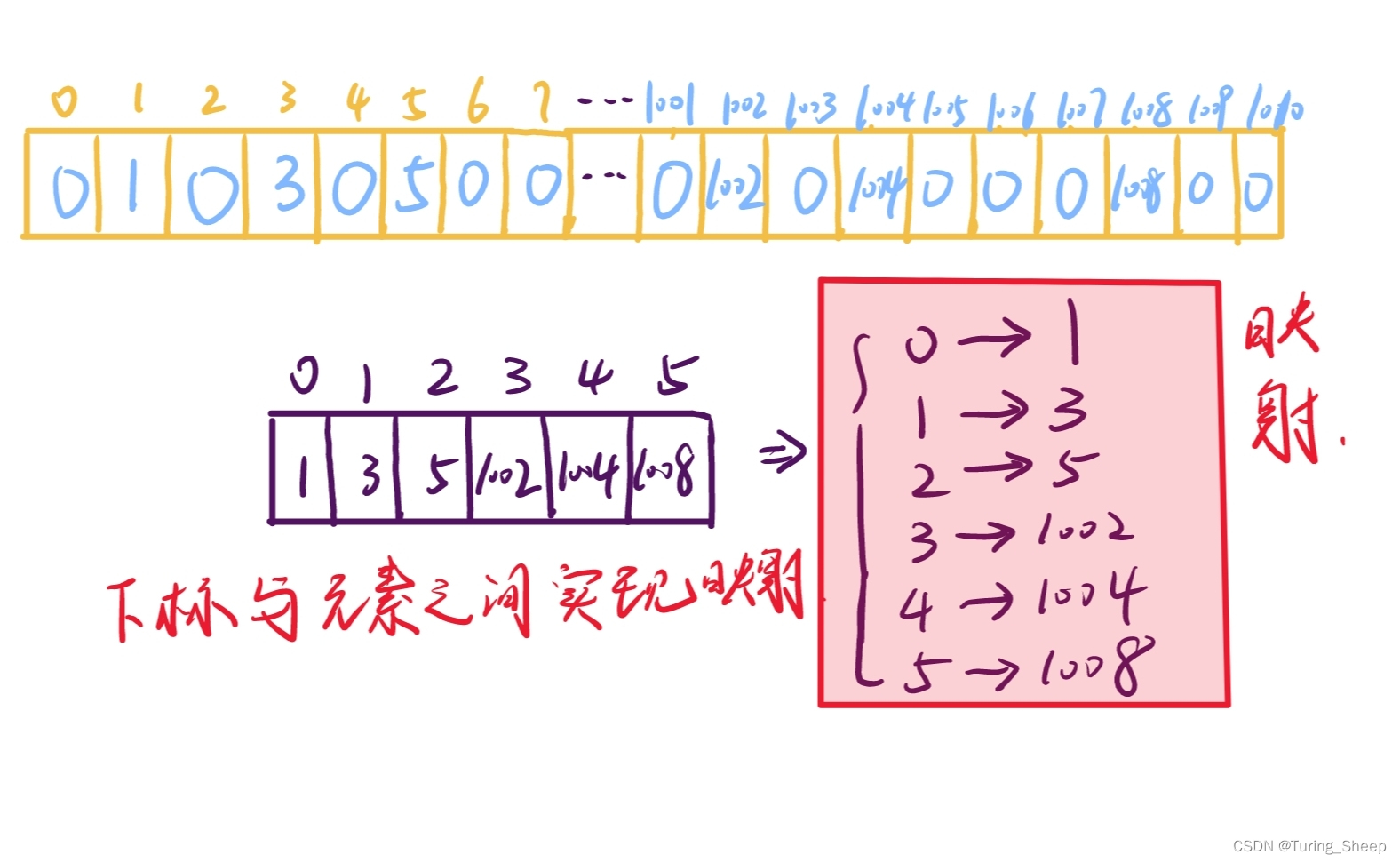
因此,实现映射的话,即将几个分散的数据去通过下表的方式聚合到一起。我们就可以通过下表访问具体的被聚合到一起的离散化数据。
但是,说到这里,大家一定还不明白为什么要实现离散化的映射?
所以我们看下面的例子:

我们看到这道题,思考五分钟后,在处理某个位置加上一个常数的操作,大家可能想到的是下面这个思路:我们开一个非常大的数组,然后通过下标来访问特定的位置,实现数值的插入。
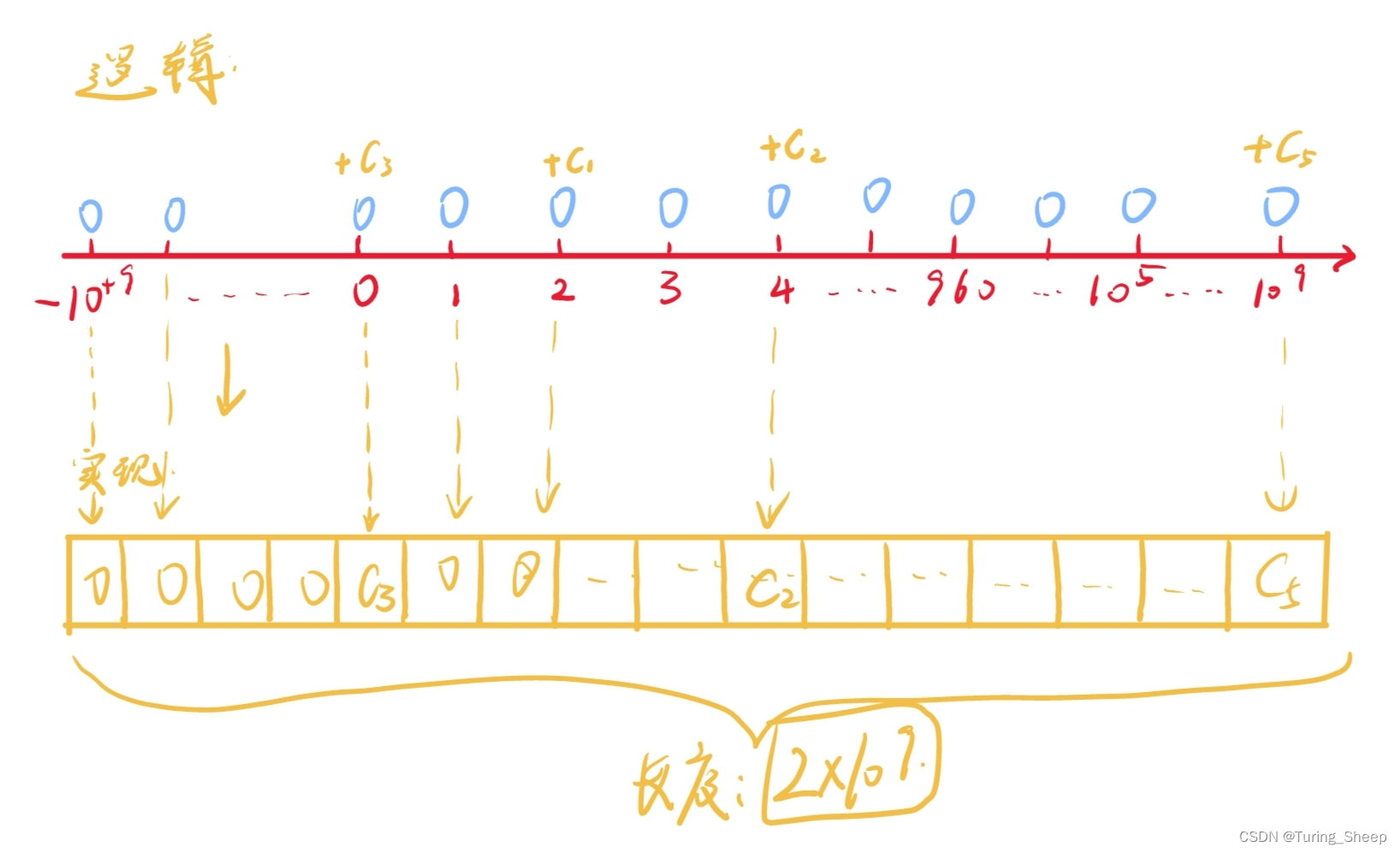
这个想法理论上是可以的,但是实现起来是非常困难的,因为我们很难在堆区去开辟这么大的一块内存。
说到这里,就需要我们所提到的**离散化映射的算法。**离散化的对象就是每次访问的下标。
具体的做题思路如下:
- 将每次插入的位置,以及最终求和的区间进行离散化映射处理。将其映射到一个数组中。
- 通过访问映射后的位置,去实现数据的插入。
- 通过前缀和运算去实现区间内的元素和。
3、模板
(1)C++
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N=3e5+10;
int a[N];
int S[N];
vector<int>alls;
vector<pair<int,int>>add,quary;
int find(int x)
{
int l=0;
int r=alls.size()-1;
while(l<r)
{
int mid=(l+r)>>1;
if(alls[mid]>=x)r=mid;
else l=mid+1;
}
return r+1;
}
int main()
{
int n,m;
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++)
{
int x,c;
scanf("%d %d",&x,&c);
add.push_back({x,c});
alls.push_back(x);
}
for(int i=0;i<m;i++)
{
int l,r;
scanf("%d %d",&l,&r);
quary.push_back({l,r});
alls.push_back(l);
alls.push_back(r);
}
sort(alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()),alls.end());
for(int i=0;i<add.size();i++)
{
int x=find((add[i]).first);
a[x]+=(add[i]).second;
}
for(int i=1;i<=alls.size();i++)
{
S[i]=S[i-1]+a[i];
}
for(int i=0;i<m;i++)
{
int l=find((quary[i]).first);
int r=find((quary[i]).second);
printf("%d\n",S[r]-S[l-1]);
}
return 0;
}
(2)C
#include <stdlib.h>
#include <stdio.h>
typedef struct pair
{
int first;
int second;
}pair;
int alls[300010];
pair add[300010];
pair quray[300010];
int a[300010];
int b[300010];
int cmp(const void*num1,const void*num2)
{
int ret=*(int*)num1-*(int*)num2;
return ret;
}
int unique(int*arr,int len)
{
int j = 0;
for(int i=0;i<len;i++)
{
if(i==0||arr[i]!=arr[i-1])arr[j++]=arr[i];
}
return j;
}
int find(int x,int len)
{
int l=0,r=len-1;
while(l<r)
{
int mid=(l+r)>>1;
if(alls[mid]>=x)r=mid;
else l=mid+1;
}
return l+1;
}
int main()
{
int n,m;
int count=0;
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++)
{
int x,c;
scanf("%d %d",&x,&c);
add[i].first=x;
add[i].second=c;
alls[count++]=x;
}
for(int i=0;i<m;i++)
{
int l,r;
scanf("%d %d",&l,&r);
quray[i].first=l;
quray[i].second=r;
alls[count++]=l;
alls[count++]=r;
}
//排序去重
qsort(alls,count,sizeof(int),cmp);
int newcount=unique(alls,count);
count=newcount;
for(int i=0;i<n;i++)
{
int p=find(add[i].first,newcount);
a[p]+=add[i].second;
}
for (int i = 1; i <= newcount; i++)
{
b[i] = b[i - 1] + a[i];
}
for(int i=0;i<m;i++)
{
int l=find(quray[i].first,newcount);
int r=find(quray[i].second,newcount);
printf("%d\n",b[r]-b[l-1]);
}
return 0;
}