在Java中计算Levenshtein莱文斯坦（相似度）编辑距离

在本教程中，我们将研究 Levenshtein 距离算法，该算法也称为编辑距离算法，用于比较单词的相似性。

什么是列文施泰因距离

Levenshtein距离算法由俄罗斯科学家Vladimir Levenshtein创建。

Levenshtein 距离算法通过计算将一个字符串转换为另一个字符串所需的最小更改/替换次数来比较单词的相似性。这些更改包括：

插入字符
删除字符
字符替换

该算法用于不同的应用或作为以下基础：

拼写检查
语音识别
基因匹配
抄袭检测

列文施泰因距离如何工作

该算法使用暴力技术将源字符串转换为目标字符串。它查看所有排列，以找到执行转换所需的最小更改数。列文施泰因距离算法也称为编辑距离算法。

例如，考虑源词狗和目标词闪避。这两个单词之间的编辑距离是 2，因为狗可以通过在 g 之前插入 d 和之后插入 e 来转换为闪避。

Levenshtein 距离算法还可以为每种类型的编辑分配不同的成本。例如，插入和删除的成本可能为 2，替换成本可能较低，成本为 1。

列文施泰因距离和动态规划

在本教程中，我们将遵循动态编程方法来实现 Levenshtein 距离算法。为了说明这种方法，我们将使用如下所示的矩阵。

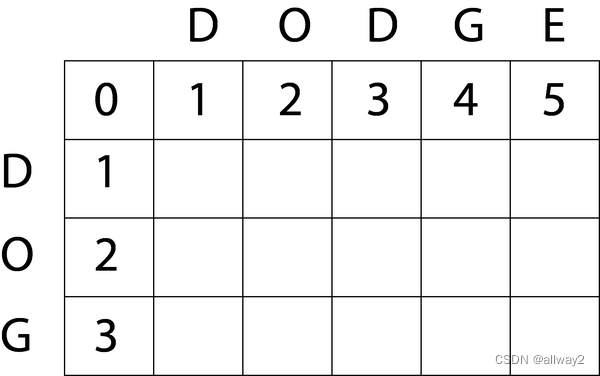
上面的矩阵使用行和列来表示源单词 dog，而目标单词 dashge。矩阵将用于计算编辑距离。矩阵的行表示要转换的源单词，其条目是插入每个字符的成本。此外，矩阵中的列用于要转换的目标单词，条目是删除的成本。

我们使用上面的矩阵来测量源词和目标词中字符之间的距离。单元格（行，列）是给定列索引处的行字符和列字符之间的距离。
矩阵将从左上角填充到右下角。
水平或垂直的每个移动都表示插入或删除。
源词和目标词之间的列文施泰因距离结果将显示在右下角。

为了计算每个单元格中的值，我们将使用一个公式，例如：

1	minCost(value of left diagonal + substitution cost, value above + deletion cost, left value + insertion cost)

我们将使用以下值作为编辑成本。

1
2
3

insertion: 1
deletion: 1
substitution: 1

此外，在上面的公式中，我们将始终将插入和删除的成本设置为 1，并且如果索引（row：col）处的字符不同，我们将仅使用替换值 1。

让我们看一个计算第一个单元格的示例。对于此单元格，位置值将为：

1
2
3

left diagonal: 0
value above: 1
left value:  1

编辑成本将为：

1
2
3

substitution: 0 – characters are the same
insertion: 1 – 1 is a constant value
deletion: 1 – 1 is a constant value

所以：

1	minCost(0 + 0, 1 + 1, 1 + 1) → min(0, 2, 2) = 0

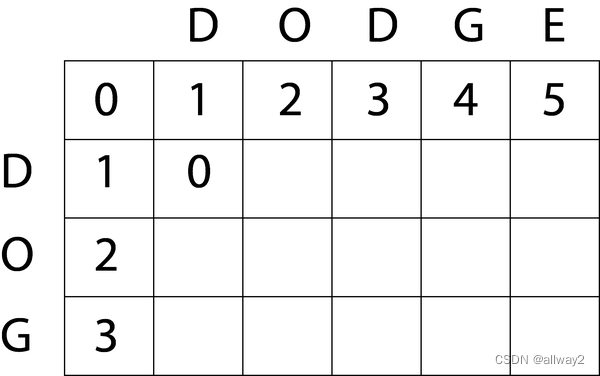
让我们继续看单元格（1，2）。对于此单元格，值将为：

1	min(1 + 1, 2 + 1, 0 + 1) → min(2, 3, 1) = 1

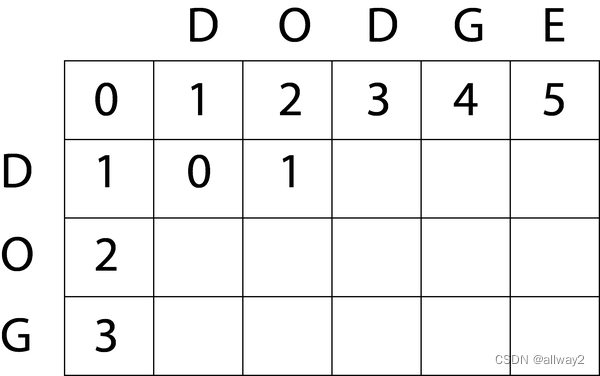
我们将继续对其余细胞进行处理。计算完这些值后，我们得到了如下所示的矩阵。

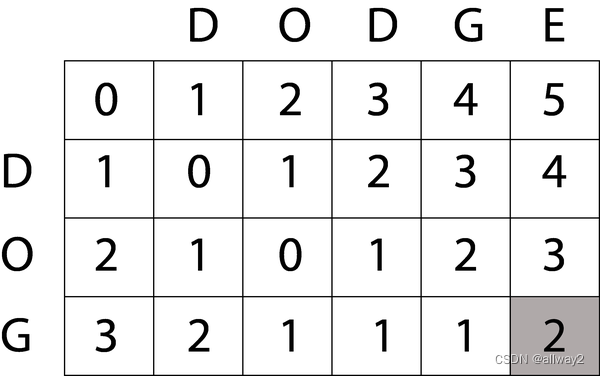
在上面的矩阵中，右下角的值是列文施泰因距离计算的结果。在这种情况下，单词 dog 和 dakge 之间的最小编辑距离为 2。

在分析上述算法时，我们可以看到该算法以二次复杂度 O（MN）执行，因为将源 M 中的每个字符与目标 N 中的每个字符进行比较以生成完全填充的矩阵。

列文施泰因距离实现

让我们编写一些代码来实现上述算法。

首先，我们将允许可配置编辑的成本：

public LevenshteinDistance(int insertionCost, int deletionCost, int substitutionCost) {
    AssertUtils.gte(insertionCost, 0, "Insertion cost must be greater than or equal to 0");
    AssertUtils.gte(deletionCost, 0, "Deletion cost must be greater than or equal to 0");
    AssertUtils.gte(substitutionCost, 0, "Substitution cost must be greater than or equal to 0");

    this.insertionCost = insertionCost;
    this.deletionCost = deletionCost;
    this.substitutionCost = substitutionCost;
}

接下来我们将编写一些代码来计算距离。

public int calculateDistance(CharSequence source, CharSequence target) {
    AssertUtils.notNull(source, "Source cannot be null");
    AssertUtils.notNull(target, "Target cannot be null");

    int sourceLength = source.length();
    int targetLength = target.length();

    int[][] matrix = new int[sourceLength + 1][targetLength + 1];
    matrix[0][0] = 0;

    for (int row = 1; row <= sourceLength; ++row) {
        matrix[row][0] = row;
    }

    for (int col = 1; col <= targetLength; ++col) {
        matrix[0][col] = col;
    }

    for (int row = 1; row <= sourceLength; ++row) {
        for (int col = 1; col <= targetLength; ++col) {
            matrix[row][col] = calcMinCost(source, target, matrix, row, col);
        }
    }

    return matrix[sourceLength][targetLength];
}

我们现在将解释上面列出的代码。在上面的代码中，我们首先使用源和目标长度初始化矩阵：

1	int[][] matrix = new int[sourceLength + 1][targetLength + 1];

我们还将矩阵行和列大小设置为比源和目标字长多 1。这样我们就可以通过添加矩阵第一行和第一列的默认值来填充空矩阵。

for (int row = 1; row <= sourceLength; ++row) {
    matrix[row][0] = row;
}

for (int col = 1; col <= targetLength; ++col) {
    matrix[0][col] = col;
}

上面的代码填充矩阵第一行和第一列的默认值。矩阵完全初始化后，下一步是计算矩阵中每个单元格的值。

for (int row = 1; row <= sourceLength; ++row) {
    for (int col = 1; col <= targetLength; ++col) {
        matrix[row][col] = calcMinCost(source, target, matrix, row, col);
    }
}

上面，我们遍历矩阵的每个单元格，计算其成本。完成此步骤后，可以在矩阵的最后一个单元格中找到最小距离：

1	return matrix[sourceLength][targetLength];

现在，让我们看看如何计算每个单元的最小成本。

private int calcMinCost(CharSequence source, CharSequence target,
                        int[][] matrix, int row, int col) {
    return Math.min(
            calcSubstitutionCost(source, target, matrix, row, col), Math.min(
                    calcDeletionCost(matrix, row, col),
                    calcInsertionCost(matrix, row, col))
    );
}

该方法查找单元格编辑的最小成本。它计算替换、插入和删除成本。此方法使用该方法返回计算成本的最小值。calcMinCostMath.min

完整的代码清单如下所示：

public class LevenshteinDistance {
    private final int insertionCost;
    private final int deletionCost;
    private final int substitutionCost;

    public LevenshteinDistance() {
        this(1, 1, 1);
    }

    public LevenshteinDistance(int insertionCost, int deletionCost, int substitutionCost) {
        AssertUtils.gte(insertionCost, 0, "Insertion cost must be greater than or equal to 0");
        AssertUtils.gte(deletionCost, 0, "Deletion cost must be greater than or equal to 0");
        AssertUtils.gte(substitutionCost, 0, "Substitution cost must be greater than or equal to 0");

        this.insertionCost = insertionCost;
        this.deletionCost = deletionCost;
        this.substitutionCost = substitutionCost;
    }

    public int calculateDistance(CharSequence source, CharSequence target) {
        AssertUtils.notNull(source, "Source cannot be null");
        AssertUtils.notNull(target, "Target cannot be null");

        int sourceLength = source.length();
        int targetLength = target.length();

        int[][] matrix = new int[sourceLength + 1][targetLength + 1];
        matrix[0][0] = 0;

        for (int row = 1; row <= sourceLength; ++row) {
            matrix[row][0] = row;
        }

        for (int col = 1; col <= targetLength; ++col) {
            matrix[0][col] = col;
        }

        for (int row = 1; row <= sourceLength; ++row) {
            for (int col = 1; col <= targetLength; ++col) {
                matrix[row][col] = calcMinCost(source, target, matrix, row, col);
            }
        }

        return matrix[sourceLength][targetLength];
    }

    private int calcMinCost(CharSequence source, CharSequence target,
                            int[][] matrix, int row, int col) {
        return Math.min(
                calcSubstitutionCost(source, target, matrix, row, col), Math.min(
                        calcDeletionCost(matrix, row, col),
                        calcInsertionCost(matrix, row, col))
        );
    }

    private int calcInsertionCost(int[][] matrix, int row, int col) {
        return matrix[row][col - 1] + insertionCost;
    }

    private int calcDeletionCost(int[][] matrix, int row, int col) {
        return matrix[row - 1][col] + deletionCost;
    }

    private int calcSubstitutionCost(CharSequence source, CharSequence target,
                                     int[][] matrix, int row, int col) {
        int cost = 0;
        if (source.charAt(row - 1) != target.charAt(col - 1)) {
            cost = substitutionCost;
        }
        return matrix[row - 1][col - 1] + cost;
    }
}

最后，我们将展示用于验证实现的测试：

@Test
public void calculateDistance() {
    LevenshteinDistance calculator = new LevenshteinDistance(1,1,1);
    final int result = calculator.calculateDistance("dog", "dodge");
    assertEquals(2,result);
}

结论

在本教程中，我们研究了 levenshtein 距离算法及其一些应用。我们还研究了使用动态规划实现它的一种方法。我们实现了一种以二次复杂度O（MN）执行的算法。因此，可以使用不同的技术来提高该算法的性能。就目前而言，该算法在相对于 O（MN）的时间内执行，因此，如果不进行一些调整，它可能不会表现出生产用例所需的性能，例如高效的拼写检查器。