题目：给定数据集dataSet，每一行代表一组数据记录,每组数据记录中，第一个值为房屋面积（单位：平方英尺），第二个值为房屋中的房间数，第三个值为房价（单位：千美元），试用梯度下降法，构造损失函数，在函数gradientDescent中实现房价price关于房屋面积area和房间数rooms的线性回归，返回值为线性方程𝑝𝑟𝑖𝑐𝑒=𝜃0+𝜃1∗𝑎𝑟𝑒𝑎+𝜃2∗𝑟𝑜𝑜𝑚𝑠中系数𝜃𝑖(𝑖=0,1,2)的列表。

%matplotlib inline

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from numpy import genfromtxt
dataPath = r"./Input/data1.csv"
dataSet = pd.read_csv(dataPath,header=None)
print(dataSet)
price = []
rooms = []
area = []
for data in range(0,len(dataSet)):
    area.append(dataSet[0][data])
    rooms.append(dataSet[1][data])
    price.append(dataSet[2][data])
print(area)

执行结果：

def gradientDescent(rooms, price, area):
    epochs = 500
    alpha = 0.00000001
    theta_gradient = [0,0,0]
    const = [1,1,1,1,1]
    theta = [1,2,1]
    loss = []
    
    for i in range(epochs):
        
        theta0 = np.dot(theta[0],const)
        theta1 = np.dot(theta[1],area)
        theat2 = np.dot(theta[2],rooms) 
        predict_tmp = np.add(theta0,theta1)
        predict = np.add(predict_tmp,theat2) 
        loss_ = predict - price
        theta_gradient[0] = (theta_gradient[0] + np.dot(const,loss_.transpose()))/5
        theta_gradient[1] = (theta_gradient[1] + np.dot(area,loss_.transpose()))/5
        theta_gradient[2] = (theta_gradient[2] + np.dot(rooms,loss_.transpose()))/5
        loss_t = np.sum(np.divide(np.square(loss_),2))/5
        if i%50==0:
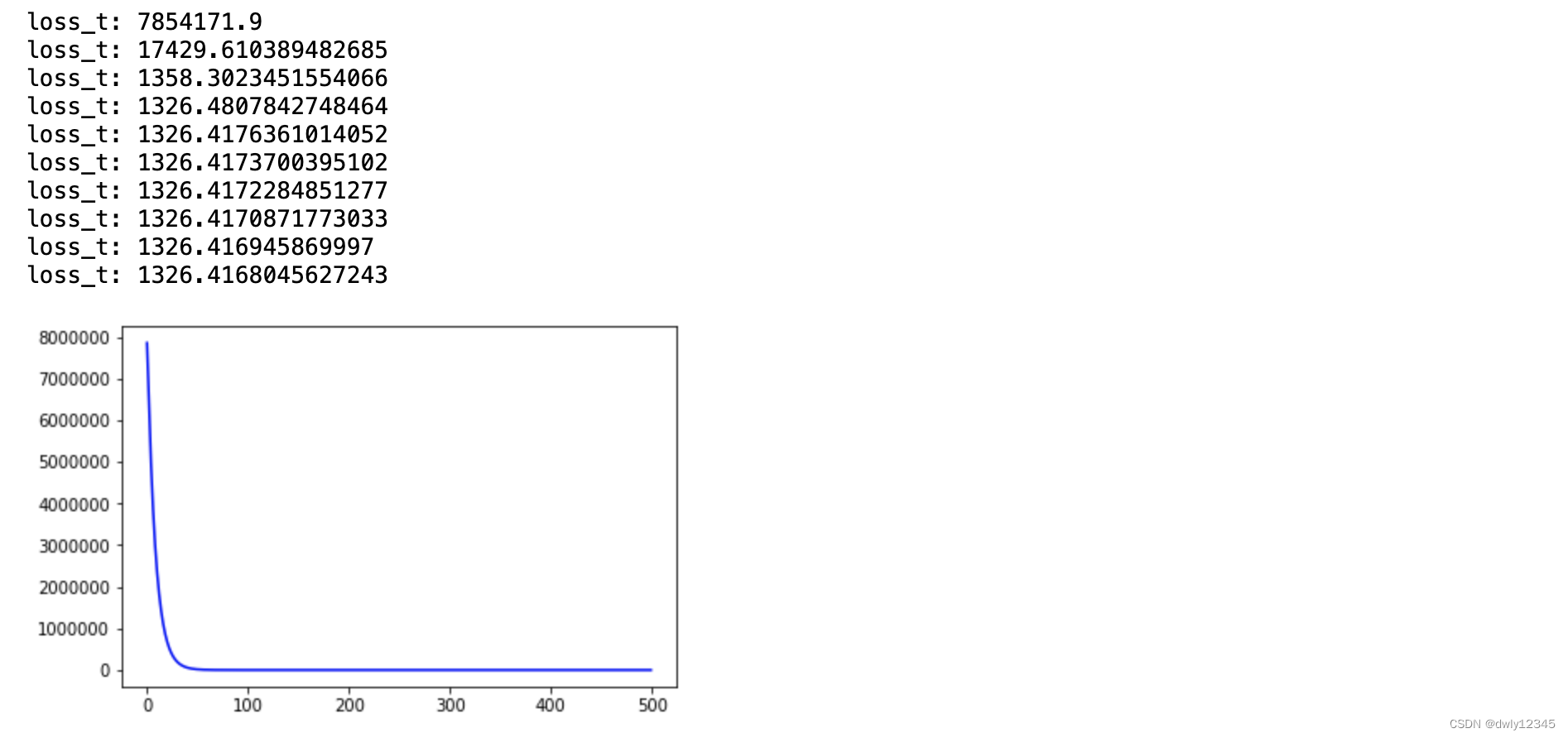
            print("loss_t:",loss_t)
        loss.append(loss_t)
        theta[0] = theta[0] - alpha * theta_gradient[0]
        theta[1] = theta[1] - alpha * theta_gradient[1]
        theta[2] = theta[2] - alpha * theta_gradient[2]
    plt.plot(loss,c='b')
    plt.show()
    return theta

def demo_GD():
    
    theta_list = gradientDescent(rooms, price, area)
demo_GD()

j结果展示：