5281. 扩展字符串
一、题目要求
某字符串序列 s0,s1,s2,… 的生成规律如下:
- s0=
DKER EPH VOS GOLNJ ER RKH HNG OI RKH UOPMGB CPH VOS FSQVB DLMM VOS QETH SQB - sn=
DKER EPH VOS GOLNJ UKLMH QHNGLNJ A+sn−1+AB CPH VOS FSQVB DLMM VOS QHNG A+sn−1+AB,其中 n≥1
你需要回答 q个询问,其中第 i 个询问给定两个整数 n,k,并请你输出字符串 sn 中的第 k 个字符(字符串中的字符索引编号从 1 开始),如果 sn 的长度小于 k,则输出 ‘.’。
输入格式
第一行包含整数 q。
接下来 q行,每行包含两个整数 n,k,表示一个询问。
输出格式
共一行,一个长度为 q 的字符串,其中第 i 个字符表示第 i 个询问的答案。
保证答案的首尾字符不是空格。
数据范围
前 3 个测试点满足 0≤n≤5。
所有测试点满足 1≤q≤10,0≤n≤10^5,1≤k≤10^18。
输入样例1:
3
1 1
1 2
1 1000000000000000000
输出样例1:
DK.
输入样例2:
5
0 69
1 194
1 139
0 47
1 66
输出样例2:
EFGHI二、思路
1.预处理字符串的长度 f[i] ,代表第i个字符串的长度
2. 通过递归找到第i个字符串长度的第k个位置的字符是多少
3.推导递归的规律

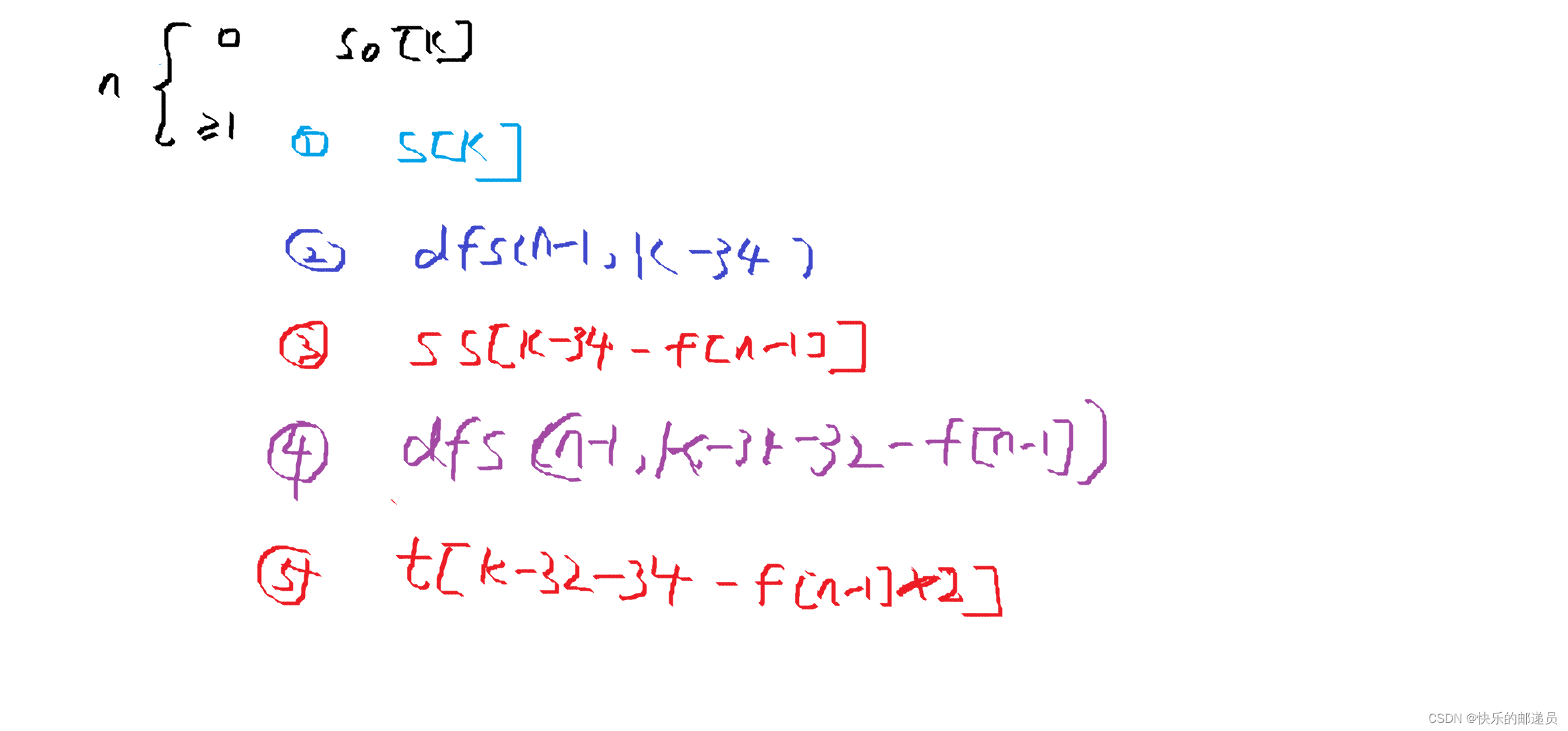
三、代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=1e5+10;
const int inf=0x3f3f3f3f;
int n,k=0;
int f[N];
string s="#DKER EPH VOS GOLNJ UKLMH QHNGLNJ A";//长度34
string ss="#AB CPH VOS FSQVB DLMM VOS QHNG A";//长度32
string t="#AB";//长度2
string s0="#DKER EPH VOS GOLNJ ER RKH HNG OI RKH UOPMGB CPH VOS FSQVB DLMM VOS QETH SQB";
//s0长度75
struct node
{
int f,x;
} q[N];
void init()//预处理字符串的长度
{
int i;
f[0]=75;
for(i=1;;i++)
{
f[i]=f[i-1]*2+68;//s+ss+s0=34+32+2=68;
if(f[i]>1e18)
break;
}
for(i++;i<=1e5;i++)//当n还未达到1e5的时候,若对应的字符串长度达到了1e18
{
f[i]=f[i-1];//让之后的字符串长度就等于接近1e18那时候的最大长度
}
}
char dfs(int n,int k)
{
if(n==0)
return s0[k];
else if(k<=34)
return s[k];
else if(k<=34+f[n-1])
return dfs(n-1,k-34);
else if(k<=34+f[n-1]+32)
return ss[k-34-f[n-1]];
else if(k<=34+32+f[n-1]*2)
return dfs(n-1,k-34-32-f[n-1]);
else
return t[k-32-34-f[n-1]*2];
}
void solve()
{
init();
cin>>n;
// cout<<"s0="<<s0.size()<<' '<<"s="<<s.size()<<' '<<"ss="<<ss.size()<<' '<<"t="<<t.size()<<endl;
int i,j;
for(i=1; i<=n; i++)
{
cin>>q[i].f>>q[i].x;
}
for(i=1;i<=n;i++)
{
if(q[i].x>f[q[i].f])
cout<<'.';
else
cout<<dfs(q[i].f,q[i].x);
}
cout<<endl;
}
signed main()
{
int t=1;
while(t--)
{
solve();
}
return 0;
}