AB试验(六)A/B实验常见知识点的Python计算
前面理论知识上提到了很多的知识点需要计算,作为一个实用主义的博主,怎么可以忍受空谈呢?所以本期就给大家分享如何利用Python对这些知识点进行计算。
均值类指标
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy import stats
import math
import seaborn as sns
from statsmodels.stats import weightstats as ws
from statsmodels.stats.proportion import proportion_effectsize
from statsmodels.stats.power import zt_ind_solve_power
from statsmodels.stats.power import tt_ind_solve_power
from statsmodels.stats.proportion import proportions_ztest
from statsmodels.stats.proportion import confint_proportions_2indep
from statsmodels.stats.multitest import multipletests
import pingouin as pg
from statsmodels.stats.proportion import proportion_effectsize
# 绘图初始化
%matplotlib inline
sns.set(style="ticks")
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
构造历史样本
# 构造数据
np.random.seed(0)
x=np.random.normal(85, 23, 1000)
plt.hist(x, 30, density=True)
plt.show()
指标波动置信区间
- 均值类指标波动置信区间=样本均值 $ \pm $z分数*标准误差(SE)
- S E = s 2 n = ∑ ( x i − x ˉ ) 2 n ( n − 1 ) SE=\sqrt\frac{s^2}{n}=\sqrt{\frac{\sum(x_i-\bar{x})^{2}}{n(n-1)}} SE=ns2=n(n−1)∑(xi−xˉ)2
# 计算均值类指标波动置信区间
def numbers_cal_ci(x, alpha=0.05):
'''
x:均值类样本
alpha:显著性水平
return:样本波动的置信区间
'''
se=np.std(x, ddof = 1)/np.sqrt(x.size) # 标准误
z=stats.norm.ppf(1-alpha/2) # z值
l=np.mean(x)-z*se
r=np.mean(x)+z*se
return [l, r]
numbers_cal_ci(x)
[82.55134770619344, 85.36684374925758]
样本量估算
- 样本量:$ n=\frac{(Z_{1-{\frac{\alpha}{2}}}+Z_{1-\beta})2}{(\frac{\delta}{\sigma_{pooled}})2}=\frac{(Z_{1-{\frac{\alpha}{2}}}+Z_{power})2}{(\frac{\delta}{\sigma_{pooled}})2} $
- $ \delta = \mu_{test} - \mu_{control}$
- $ \sigma_{pooled}^2 = 2S^2 = \frac{2*\sum_{i}^{n}(x_i - \bar x)^2}{n-1} $ (以样本方差代替综合方差)
# 公式法计算样本量
def numbers_cal_sample(u1, u2, s, alpha=0.05, beta=0.2):
'''
u1:对照组均值
u2:实验组均值
s:样本标准差(历史数据计算得出)
alpha:显著性水平,默认为0.05
beta:默认为0.2
return:均值类指标样本量
'''
z1=stats.norm.ppf(1-alpha/2)
z2=stats.norm.ppf(1-beta)
delta=u2-u1
sigma2=2*s**2
n=(z1+z2)**2/(delta**2/sigma2)
return math.ceil(n)
s=np.std(x, ddof = 1)
u1=85
u2=86
print(numbers_cal_sample(u1,u2,s))
# 第三方包计算样本量
def numbers_cal_sample_third(u1, u2, s, alpha=0.05, beta=0.2, ratio=1, alternative="two-sided"):
'''
u1:对照组均值
u2:实验组均值
s:样本标准差(历史数据计算得出)
alpha:显著性水平,默认为0.05
beta:默认为0.2
ratio:对照组/实验组的比例
alternative:检验方式[two-sided(default), larger, smaller]
return:均值类指标样本量
'''
effect_size=(u2-u1)/s
n=tt_ind_solve_power(effect_size=effect_size,
alpha=alpha,
power=1-beta,
ratio=ratio,
alternative=alternative)
return math.ceil(n)
print(numbers_cal_sample_third(u1,u2,s))
8099
8100
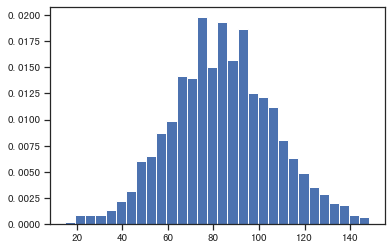
构造A/B实验样本
# 构造实验数据
np.random.seed(1)
control=np.random.normal(85.1, 23, 8108)
test=np.random.normal(86.01, 22.8, 8110)
sns.kdeplot(test, color='g', linestyle='-', linewidth=1.2, alpha=0.5)
sns.kdeplot(control, color='r', linestyle='--', linewidth=1.2, alpha=0.5)
plt.show()
样本比例校验
- 样本比例服从二项分布
- 概率类指标置信区间=样本均值 $ \pm $z分数*标准误差(SE)
- S E = p ( 1 − p ) n SE=\sqrt{\frac{{p}(1-{p})}{n}} SE=np(1−p)
# 样本比例校验
def two_sample_proportion_test(n1, n2, p1, p2, alpha=0.05):
'''
n1:对照组实际样本量
n2:实验组实际样本量
p1:对照组预设样本比例
p2:实验组预设样本比例
alpha:显著性水平
return:(对照组样本比例置信区间,实验组样本比例置信区间)
'''
se=np.sqrt((p1*p2)/(n1+n2))
z=stats.norm.ppf(1-alpha/2)
# 计算两组样本比例置信区间
control_prob=[p1-z*se, p1+z*se]
test_prob=[p2-z*se, p2+z*se]
# 计算实际两组样本比例
control_prob_real=n1/(n1+n2)
test_prob_real=n2/(n1+n2)
# 判断样本比例是否在置信区间内
if control_prob_real>=control_prob[0] and control_prob_real<=control_prob[1]:
control_flag=1
else:
control_flag=0
if test_prob_real>=test_prob[0] and test_prob_real<=test_prob[1]:
test_flag=1
else:
test_flag=0
# 判断是否检验通过
if control_flag==1&test_flag==1:
print('两样本比例校验: 通过')
else:
print('两样本比例校验不通过')
print(f'对照组样本比例置信区间:{control_prob}', f'对照组实际样本比例:{control_prob_real}')
print(f'实验组样本比例置信区间:{test_prob}', f'实验组实际样本比例:{test_prob_real}')
n1=control.size
n2=test.size
p1=p2=0.5
two_sample_proportion_test(n1, n2, p1, p2)
两样本比例校验: 通过
特征一致性校验
详见下面的特征分布一致性校验
计算效应量
# 公式法计算效应量
def numbers_cal_es(x, y):
'''
x:对照组样本
y:实验组样本
return: cohen d方法计算的效应量es
'''
n1, n2 = len(x), len(y)
s1, s2 = np.var(x, ddof=1), np.var(y, ddof=1)
s = math.sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))
u1, u2 = np.mean(x), np.mean(y)
return (u1 - u2) / s
# 第三方包计算效应量
def numbers_cal_es_third(x, y):
'''
x:对照组样本
y:实验组样本
return: cohen d方法计算的效应量es
'''
return pg.compute_effsize(x, y, eftype='cohen')
# 输入参数为统计量
def numbers_cal_es_stats(u1, s1, n1, u2, s2, n2):
'''
n1:对照组样本量
n2:实验组样本量
s1:对照组样本方差
s2:实验组样本方差
u1:对照组均值
u2:实验组均值
return: cohen d方法计算的效应量es
'''
s = math.sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))
return (u1 - u2) / s
numbers_cal_es_third(test, control)
0.04827141870721603
- 样本大小、显著性水平、功效、效应值,给定任意三个值,可以推算出第四个值。这里的 e s = δ σ p o o l e d es=\frac{\delta}{\sigma_{pooled}} es=σpooledδ
- 在A/B/n实验中,通过比较不同实验组与对照组的效应值大小选择最优实验组。
显著性检验
# 均值类指标检验,输出t统计量,p值,差值的置信区间
def numbers_cal_significant(x, y, alpha=0.05, alternative='two-sided', levene_print=True):
'''
x:实验组样本
y:对照组样本
alpha:显著性水平
return:t统计量,p值,差异值的置信区间
'''
levene_p=stats.levene(x, y)[1]
if levene_p>alpha:
equal_var=True
usevar='pooled'
if levene_print:
print('方差齐性校验结果:方差相同')
else:
equal_var=False
usevar='unequal'
if levene_print:
print('方差齐性校验结果:方差不同')
# 计算检验统计量及p值
t, p = stats.ttest_ind(x, y, alternative=alternative, equal_var=equal_var)
# 计算置信区间
des1=ws.DescrStatsW(x)
des2=ws.DescrStatsW(y)
comp=ws.CompareMeans(des1, des2)
l, r=comp.tconfint_diff(alpha=alpha, alternative=alternative, usevar=usevar)
return (t, p , [l, r])
# 输入参数为统计量 忽略方差齐性检验(认为方差未知但相同)
def numbers_cal_significant_stats(u1, s1, n1, u2, s2, n2, alpha=0.05):
'''
n1:对照组样本量
n2:实验组样本量
s1:对照组样本方差
s2:实验组样本方差
u1:对照组均值
u2:实验组均值
'''
# 计算检验统计量及p值
std1, std2 = math.sqrt(s1), math.sqrt(s2)
t, p = stats.ttest_ind_from_stats(u1, std1, n1, u2, std2, n2)
# 计算置信区间
mu_diff = u1-u2
df = n1+n2-2
sw = np.sqrt(((n1-1)*s1+(n2-1)*s2)/df)
d = sw*np.sqrt(1/n1+1/n2)
tl, tr = stats.t.interval(1-alpha, df)
l, r = mu_diff+tl*d, mu_diff+tr*d
return (t, p , [l, r])
print(numbers_cal_significant(test, control))
u1, u2 = np.mean(test), np.mean(control)
n1, n2 = len(test), len(control)
s1, s2 = np.var(test, ddof=1), np.var(control, ddof=1)
print(numbers_cal_significant_stats(u1, s1, n1, u2, s2, n2))
方差齐性校验结果:方差相同
(3.0736804306795347, 0.0021178678616854507, [0.40032026505442575, 1.8096106890034274])
(3.0736804306795347, 0.0021178678616854507, [0.4003202650543972, 1.809610689003399])
在日常业务中,考虑到样本数据量过大,一般会直接计算好样本统计量。
概率类指标
构造历史样本
# 构造数据
x=stats.bernoulli.rvs(0.4, size=10000, random_state=0)
plt.hist(x, 30, density=True)
plt.show()

指标波动置信区间
- 概率类指标置信区间=样本均值 $ \pm $z分数*标准误差(SE)
- S E = p ( 1 − p ) n SE=\sqrt{\frac{{p}(1-{p})}{n}} SE=np(1−p)
# 计算概率类指标置信区间
def prob_cal_ci(p, n, alpha=0.05):
'''
p1:样本概率
alpha:显著性水平
return:样本波动的置信区间
'''
se=np.sqrt((p*(1-p))/n)
z=stats.norm.ppf(1-alpha/2)
l=p-z*se
r=p+z*se
return [l, r]
p=np.mean(x)
n=x.size
prob_cal_ci(p, n)
[0.38462208374405027, 0.4037779162559497]
样本量估算
- 样本量:$ n=\frac{(Z_{1-{\frac{\alpha}{2}}}+Z_{1-\beta})2}{(\frac{\delta}{\sigma_{pooled}})2}=\frac{(Z_{1-{\frac{\alpha}{2}}}+Z_{power})2}{(\frac{\delta}{\sigma_{pooled}})2} $
- $ \delta = \mu_{test} - \mu_{control}$
- $ \sigma_{pooled}^2=p_{test}(1-p_{test})+p_{control}(1-p_{control}) $
- $ p_{test}=p_{control}+\delta $
# 公式法计算样本量
def prob_cal_sample(p1, p2, alpha=0.05, beta=0.2):
'''
p1:对照组均值
p2:实验组均值
alpha:显著性水平,默认为0.05
beta:默认为0.2
return:概率类指标样本量
'''
z1=stats.norm.ppf(1-alpha/2)
z2=stats.norm.ppf(1-beta)
delta=p2-p1
sigma2=p2*(1-p2)+p1*(1-p1)
n=(z1+z2)**2/(delta**2/sigma2)
return math.ceil(n)
# 第三方包计算样本量
def prob_cal_sample_third(p1, p2, alpha=0.05, beta=0.2, ratio=1, alternative="two-sided"):
'''
p1:对照组均值
p2:实验组均值
alpha:显著性水平,默认为0.05
beta:默认为0.2
ratio:对照组/实验组的比例
alternative:检验方式[two-sided(default), larger, smaller]
return:均值类指标样本量
'''
effect_size=proportion_effectsize(prop1=p1, prop2=p2)
n=zt_ind_solve_power(effect_size=effect_size,
alpha=alpha,
power=1-beta,
ratio=ratio,
alternative=alternative)
return math.ceil(n)
p1=0.39
p2=0.42
print(prob_cal_sample(p1, p2))
print(prob_cal_sample_third(p1, p2))
4200
4202
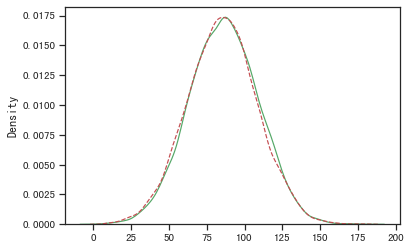
构造A/B实验样本
# 构造实验数据
control=stats.bernoulli.rvs(0.401, size=4203, random_state=1)
test=stats.bernoulli.rvs(0.433, size=4206, random_state=1)
plt.hist(control, 30, color='g', linestyle='-')
plt.hist(test+0.03, 30, color='r', linestyle='--')
plt.show()
样本比例校验
# 样本比例校验
n1=control.size
n2=test.size
p1=p2=0.5
two_sample_proportion_test(n1, n2, p1, p2)
两样本比例校验: 通过
特征一致性校验
详见下面的特征分布一致性校验
计算效应量
# 公式法计算效应量
def prob_cal_es(p1, p2):
return 2*(np.arcsin(math.sqrt(p1)) - np.arcsin(math.sqrt(p2)))
# 第三方包计算效应量
def prob_cal_es_third(p1, p2):
return proportion_effectsize(p1, p2)
p1, p2 = np.mean(test), np.mean(control)
prob_cal_es_third(p1, p2)
0.06779547842527989
显著性检验
# 概率类指标检验,输出z统计量,p值,差值的置信区间
# 手动计算两比例样本置信区间
def two_proprotions_confint(count1, nobs1, count2, nobs2, alpha=0.05):
'''
count1:转化次数1
nobs1:观察次数1
count2:转化次数2
nobs2:观察次数2
alpha:显著性水平
return:置信区间
'''
prop_x=count1/nobs1
prop_y=count2/nobs2
s2=prop_x*(1-prop_x)/nobs1+prop_y*(1-prop_y)/nobs2
se=np.sqrt(s2)
# 计算z
confidence=1-alpha
z=stats.norm(loc=0, scale=1).ppf(confidence+alpha/2)
# 计算置信区间
prop_diff = prop_x - prop_y
l=prop_diff-z*se
r=prop_diff+z*se
return (l, r)
def prob_cal_significant(count1, nobs1, count2, nobs2, alpha=0.05):
'''
count1:转化次数1
nobs1:观察次数1
count2:转化次数2
nobs2:观察次数2
alpha:显著性水平
return:z统计量,p值,差异值的置信区间
'''
counts=np.array([count1,count2])
nobs=np.array([nobs1,nobs2])
# 计算检验统计量及p值
z, p=proportions_ztest(counts, nobs)
# # 计算置信区间
# l,r=two_proprotions_confint(count1, nobs1, count2, nobs2, alpha=alpha)
# 第三方包计算
l,r=confint_proportions_2indep(count1, nobs1, count2, nobs2, alpha=alpha)
return (z, p , [l, r])
count1=test.sum()
nobs1=test.size
count2=control.sum()
nobs2=control.size
prob_cal_significant(count1, nobs1, count2, nobs2)
(3.1077966572498585,
0.0018848770736162972,
[0.012362934368799147, 0.054539748981100436])
Bootstrapping
指标波动置信区间
- 多次重复抽样得到样本均值的分布
- 通过经验法(百分位法),即按样本均值大小排序剔除前后
2.5%的区间作为置信区间- 同样本多次AA实验计算置信区间类似,实践中更多应用Bootstrapping法,故不做详述
# 构造单样本数据
np.random.seed(0)
bt=np.random.randint(10, 5000, 10000)
plt.hist(bt, 30, density=True)
plt.show()
# 定义单次抽样函数
def bootstrap_one(data, leng=100, func=np.mean):
'''
data:数据
leng:抽样长度,大于0的数,当长度为(0,1)间的浮点数时,定义为抽样比例。
func:计算函数,默认为均值
return:一次抽样的函数计算结果
'''
leng=int(leng*len(data)) if leng<1 else int(leng)
bs_sample=np.random.choice(data, leng)
return func(bs_sample)
# bootstrap计算指标波动置信区间
def bootstrap_cal_ci(data, leng=100, func=np.mean, scale=100, alpha=0.05):
'''
data:数据
leng:抽样长度,大于0的数,当长度为(0,1)间的浮点数时,定义为抽样比例。
func:计算函数,默认为均值
scale:抽样次数
alpha:显著性水平
return:置信区间和标准误
'''
bs_result=np.empty(scale)
for i in range(scale):
np.random.seed(i)
bs_result[i]=bootstrap_one(data)
l,r=np.percentile(bs_result, [alpha/2*100, (1-alpha/2)*100])
se=np.std(bs_result) # 输出多次抽样均值的标准差,即抽样均值标准误
return ([l,r], se)
bootstrap_cal_ci(bt, scale=10000)
([2223.547, 2792.2925], 144.78451383376327)
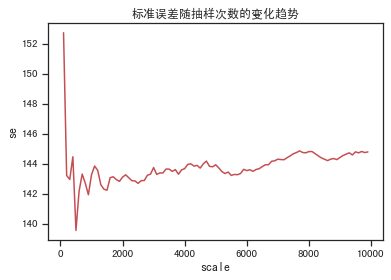
# 观察标准误 随着抽样次数的增多逐渐趋于稳定
x=[]
se=[]
for i in range(100, 10000, 100):
x.append(i)
se.append(bootstrap_cal_ci(bt, scale=i)[1])
plt.plot(x, se, 'r-')
plt.title('标准误差随抽样次数的变化趋势')
plt.xlabel('scale')
plt.ylabel('se')
plt.show()
指标差值置信区间
# 构造两样本数据
np.random.seed(1)
test=np.random.randint(10, 200, 9997)
control=np.random.randint(30, 120, 10003)
plt.subplot(1, 2, 1)
plt.hist(test, 30, density=True)
plt.subplot(1, 2, 2)
plt.hist(control, 30, density=True)
plt.tight_layout()
plt.show()
# bootstrap计算样本差值置信区间
def bootstrap_cal_ci_2samples(x, y, leng=100, func=np.mean, scale=100, alpha=0.05):
'''
x:数据1
y:数据2
leng:抽样长度,大于0的数,当长度为(0,1)间的浮点数时,定义为抽样比例。
func:计算函数,默认为均值
scale:抽样次数
alpha:显著性水平
return:置信区间
'''
bs_diff=np.empty(scale)
for i in range(scale):
np.random.seed(i)
bs_diff[i]=bootstrap_one(x)-bootstrap_one(y)
# 计算差异的置信区间
l,r=np.percentile(bs_diff, [alpha/2*100, (1-alpha/2)*100])
return [l,r]
bootstrap_cal_ci_2samples(test, control, scale=10000)
[18.939500000000013, 42.65124999999999]
多重检验问题校正
def multiple_tests_adjust(pvalues, method='fdr_bh', alpha=0.05):
'''
pvalues:p值序列
method:校正方式,默认为bh法
alpha:需比较的显著性水平,默认为0.05
return:(拒绝H0的结果序列, 校正后的p值序列, Bonferroni校正的alpha)
'''
result=multipletests(pvalues, method=method, alpha=alpha)
reject=result[0]
adjust_p=result[1]
adjust_alpha=result[3] # Bonferroni方法
return reject,adjust_p,adjust_alpha
pvalues=[0.02, 0.03, 0.18, 0.04, 0.002, 0.005]
multiple_tests_adjust(pvalues)
(array([ True, True, False, True, True, True]),
array([0.04 , 0.045, 0.18 , 0.048, 0.012, 0.015]),
0.008333333333333333)
特征分布一致性校验
实践中往往需要保证不同样本特征分布是相似的,例如A/B中的实验组和对照组、机器学习的训练集和测试集等
数据准备
from faker import Faker
from faker.providers import BaseProvider, internet
from random import randint
from scipy.stats import bernoulli
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from scipy import stats
from scipy.stats import kstest
from scipy.stats import ks_2samp
from collections import defaultdict
import toad
import matplotlib.pyplot as plt
import seaborn as sns
# 绘图初始化
%matplotlib inline
sns.set(style="ticks")
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 自定义数据
fake = Faker('zh_CN')
class MyProvider(BaseProvider):
def myCityLevel(self):
cl = ["一线", "二线", "三线", "四线+"]
return cl[randint(0, len(cl) - 1)]
def myGender(self):
g = ['F', 'M']
return g[randint(0, len(g) - 1)]
def myDevice(self):
d = ['Ios', 'Android']
return d[randint(0, len(d) - 1)]
fake.add_provider(MyProvider)
# 构造假数据
uid=[]
cityLevel=[]
gender=[]
device=[]
age=[]
activeDays=[]
for i in range(100000):
uid.append(i+1)
cityLevel.append(fake.myCityLevel())
gender.append(fake.myGender())
device.append(fake.myDevice())
age.append(fake.random_int(min=18, max=65))
activeDays.append(fake.random_int(min=0, max=180))
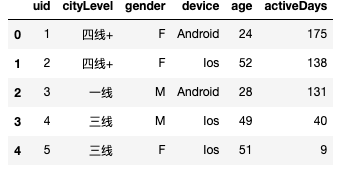
raw_data= pd.DataFrame({'uid':uid,
'cityLevel':cityLevel,
'gender':gender,
'device':device,
'age':age,
'activeDays':activeDays,
})
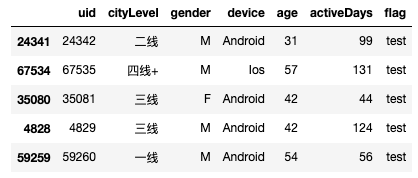
raw_data.head()
模拟A/B实验分流
# 数据随机切分,模拟实验分流
test, control= train_test_split(raw_data.copy(), test_size=.5, random_state=0)
test['flag'] = 'test'
control['flag'] = 'control'
df = pd.concat([test, control])
df.head()
数据探索
# 查看离散变量的分布
fig, ax =plt.subplots(1, 3, constrained_layout=True, figsize=(12, 3))
for i, x in enumerate(['cityLevel', 'gender', 'device']):
sns.countplot(x=x, data=df, hue='flag', ax=ax[i])
plt.show()
# 查看连续变量的分布
fig, ax =plt.subplots(1, 2, constrained_layout=True, figsize=(12, 3))
for i, x in enumerate(['age', 'activeDays']):
sns.histplot(x=x, data=df, hue='flag', ax=ax[i])
plt.show()
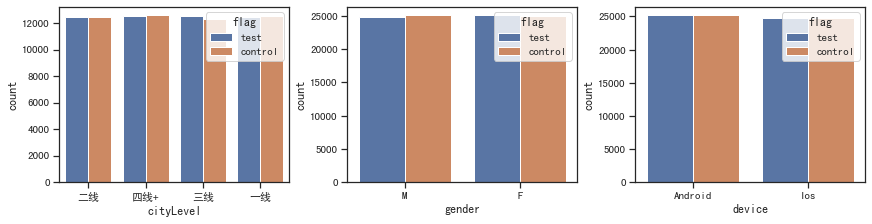
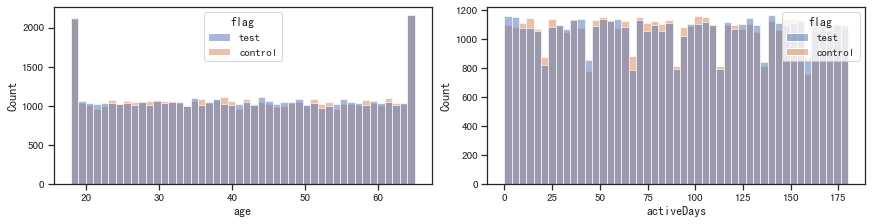
- 构造数据是随机的,因此在不同维度上表现的基本都是取值概率相等。这里目的是验证特征分布的一致性,暂不考虑实际业务场景
- 整体上看实验、对照组在各特征上的分布接近
样本相似性校验
卡方检验
- 通过列联表检验不同离散变量对分组是否有影响
- 将连续变量分箱为离散变量
# 连续变量离散化
df['age_bins'] = pd.qcut(df['age'], q=5, labels=range(5))
df['activeDays_bins'] = pd.cut(df['activeDays'], bins=[-1, 20, 120, 180], labels=['低', '中', '高'])
for x in ['cityLevel', 'gender', 'device', 'age_bins', 'activeDays_bins']:
df_ = pd.pivot_table(df, values = ['uid'], index = [x], columns='flag', aggfunc = 'count')
chi2, p, _, _, = stats.chi2_contingency(df_)
print(f'{x}:','不相似' if p<0.05 else '相似')
cityLevel: 相似
gender: 相似
device: 相似
age_bins: 相似
activeDays_bins: 不相似
KS检验
- 检验一个分布f(x)与理论分布g(x)是否一致
- 两个观测值分布是否有显著差异的检验方法
# 验证样本是否符合正态分布
# P值远小于显著性水平,拒绝原假设,即不服从正态分布
kstest(df['age'], 'norm')
KstestResult(statistic=1.0, pvalue=0.0)
# 回归正题,验证两样本分布是否一致
for x in ['cityLevel', 'gender', 'device', 'age', 'activeDays']:
_, p = ks_2samp(test[x], control[x])
print(f'{x}:','不相似' if p<0.05 else '相似')
cityLevel: 相似
gender: 相似
device: 相似
age: 相似
activeDays: 不相似
相对熵
- KL散度是用于衡量分布P相对于分布Q的差异性。二者越相似,KL散度越小。
- 同kl散度,JS散度的取值范围在0-1之间,完全相同时为0。
def JS_divergence(p,q):
M=(p+q)/2
return 0.5*stats.entropy(p, M, base=2)+0.5*stats.entropy(q, M, base=2)
# 连续变量离散化
df['age_bins'] = pd.qcut(df['age'], q=5, labels=range(5))
df['activeDays_bins'] = pd.cut(df['activeDays'], bins=[-1, 20, 120, 180], labels=['低', '中', '高'])
for x in ['cityLevel', 'gender', 'device', 'age_bins', 'activeDays_bins']:
a=df[df['flag']=='test'][x].value_counts()/df[df['flag']=='test'].size
b=df[df['flag']=='control'][x].value_counts()/df[df['flag']=='control'].size
print(f'{x} KL:', round(stats.entropy(a, b),4), '/', 'JS: ', round(JS_divergence(a, b),4))
cityLevel KL: 0.0 / JS: 0.0001
gender KL: 0.0 / JS: 0.0
device KL: 0.0 / JS: 0.0
age_bins KL: 0.0 / JS: 0.0
activeDays_bins KL: 0.0001 / JS: 0.0
PSI
- PSI反映了验证样本在各分数段的分布与建模样本分布的稳定性。在建模中,我们常用来筛选特征变量、评估模型稳定性
- 可以用来衡量两个分布的差异有多大,当两个随机分布完全一样时,PSI = 0;反之,差异越大,PSI越大。类似于相对熵
- 一半psi<0.02为稳定
toad.metrics.PSI(test.iloc[:,1:-1], control.iloc[:,1:-1])
cityLevel 0.000075
gender 0.000054
device 0.000003
age 0.001624
activeDays 0.007159
dtype: float64
总结
本文基本涵盖了A/B实验过程中的所有计算,因此将这些函数全部保存在ABTestFunc.py中,即可构造属于自己的AB测试模块~
共勉~