【码制】原码反码补码移码浮点数

从C语言占位符到码值

学C语言的时候一定会用到printf("%d",a);
有的课程称%d为“占位符”，非常形象：%d替a占位，输出的时候a的值会替换%d的内容。
但也有课程称之为“转换规范”，官方称之为“format specifiers”格式说明符。
以我目前的文化水平，我更倾向于“转换规范”。
因为计算机中的数据都是以01的形式存储，你不知道这串01是什么意思。
以char类型的变量a为载体举个例子：

unsigned char a=-1;
//-1      255     ff
printf("%hhd\t%hhu\t%hhx", a, a, a);

无符号数应该是不支持负数的，但上面的代码并不会报错，可以正常输出。
以hhd的方式输出的就是-1，以hhx的方式输出的就是ff。hhx的意思是，输出1个字节宽度的十六进制表示，输出的内容是ff，对应二进制就是1111 1111。
如果你用hhu的方式输出，也就是1个字节宽度的无符号数，输出内容将是255，也就是二进制数1111 1111的十进制表示。
对于二进制内容1111 1111：

如果当成补码表示，那么真值就是-1。
如果当成纯二进制表示，也就是无符号数，那么真值就是255。

你可能会有以下疑问：

无符号数只有正数，但可以被负数赋值。
-1可以被解释成255，255也可以被解释成-1。

甚至即使你再加上1，人为地产生进位，程序也不会报错。

从正数加减法到负数加减法

如果有这样一个运算需求：0+1

你会知道结果是1，如果用八位二进制表示，那就是：

0000 0000+0000 0001=0000 0001

如果是0+2呢，那就是：

0000 0000+0000 0010=0000 0010

正数的情况看起来非常简单，那如果是255+1呢，也就是：

1111 1111+0000 0001=1 0000 0000

由于存储单元大小为8位，产生了进位，存储单元最后保存的是0000 0000。

如果要计算0-1呢？

到目前为止，我们没有涉及二进制减法的内容，实际上也不需要了解减法的运算规则。
假设计算的结果是x，那么0-1=x就可以变成0=x+1。
也就是说，我们需要找一个+1后等于1 0000 0000的数，而这个数前面已经出现了，也就是1111 1111，十六进制表示就是0xff，也就是-1的补码表示。
也就是说，-1的补码就等于0减1，就是找一个加1之后等于0的数X，这个数X的二进制表示就是-1的补码。
那如果是-2呢，那就是找一个加2之后等于0的数，也就是1111 1110。
以此类推。并且你会发现：

只要减数不是太大，小于128，最多减到1000 0000，最高位始终为1。
只要加数不是太大，小于127，最多加到0111 1111，最高位始终为0。

8位二进制共有 $2^8=256$ 种01序列，以最高位为符号位，去掉最高位之后还有 $2^7=128$ 种01序列，也就是说：

符号位1开头的有128个，即有128个负数。
符号位0开头的有128个，即有128个非负数，由于0还占一个，所以有127个正数。

我们人为地将添加一个偏移量，使得0x80到0xff的二进制数映射到负数-128到127上。使得原本的十进制数128到255分别表示-128到127。
有符号数 X 与补码的转换公式如下，256是8位二进制数的计数周期。
$[X]_补=\left\{ \begin{aligned} &X\quad X>=0\\ &X+256 \quad X<0 \end{aligned}\right.$

原码？反码？

原码：没啥用。
反码：没啥用
原码和反码是人工求补码的中间过程。
计算机正负数补码的转换只有“减一取反”。
中间不保留原码和反码，计算机也不考虑这些。
学校的课件上说浮点数的尾数用原码表示，但在“软件设计师”中，尾数通常是用补码表示的。

移码

移码：数值上等于补码的最高位取反。
补码中小于零和大于等于零的数各占一半，有128个。最小的数是从1000 0000开始的，表示-128。
移码则是从0000 0000开始计最小的数，也表示-128。

与有符号数X的关系是： $X]_移=X+128$
其中，128是二进制数计数周期的一半。
在补码中，1111 1111表示-1，0000 0000表示0。1111 1111表示的数比0000 0000表示的数要小。这有点乱。
在移码中，1111 1111表示127，0000 0000表示-128。较大的有符号数，对应的移码也是较大的。
因此，在比较数值大小和求差值的时候，是可以直接用移码相减的。
也因此，浮点数的阶码要用移码表示：方便比较、方便求差值对阶。

但，浮点数移码的偏移量不是128，而是127。

在这里，移码的偏移量是128，是因为8位二进制数计数周期的一半是128，也就是 $2^7$
如果是32位二进制数，那么偏移量将是 $2^{31}$ 。
如果你还是对偏移量不太清楚，那么本文的后面会有更详细的介绍。

四种码值的转换

如果现在有一个需求：求-128的补码。
如果是“求反加一”的方法，将会不知所措。
如果用上面的方法： $[X]_补=\left\{ \begin{aligned} &X\quad X>=0\\ &X+256 \quad X<0 \end{aligned}\right.$
则会轻松的多：-128的补码就等于十进制数128的二进制表示。
求-128的移码呢？那就是： $X]_移=X+128$
-128的移码就等于十进制数0的二进制表示。
求-128的原码呢？求不了，没有。
求-128的反码呢？求不了，没有。
如果非要求出一个的话，那就只能用偏移量的方法。并且在软件设计师的教材中，解题用的往往都是“偏移量”，而不是“取反加一”。我个人也更倾向于使用“偏移量”。
因为原码和反码本身只是个中间产物，计算机中不存储它们，因此除了考试没啥用处。
正数的三种码制相同。
已知真值的情况下，对负数：

原码：绝对值对应的二进制，最高位置1。
反码：除了最高位，按位取反。

已知补码的情况下，对负数：

原码：减一求反
反码：补码减一

已知移码的情况下，先转换为补码。

定点数到浮点数

上面只是说了整数的表示。
如果是小数呢？分为定点小数和浮点小数。
在表示整数的时候，我们默认了有个小数点，在01串的最右边，这被称为定点整数。
如果要表示定点小数，那么默认有个小数点，在01串的最左边。
比如1100 0000表示 $2^{-1}+2^{-2}=0.5+0.25=0.75$ 。
从左到右分别对应2的-1、-2…次幂，为什么要人为规定成这样呢，这跟二进制运算有关。
假如现在默认小数点位置在中间，有10.00表示2。
01.00表示1，满足2/2=1，由2的二进制表示右移一位得到。
00.10应该表示1/2=0.5，由1的二进制表示右移一位得到。
00.01应表示0.5/2=0.25，也就是 $2^{-2}$ 。

浮点数表示

如果用十进制，浮点数可以表示成： $尾数\times10^{阶码}$

阶码：决定数值范围
尾数：决定数值精度

计算机用的是二进制，那么把10替换成2即可： $尾数\times2^{阶码}$
为了充分利用尾数，需要采用规格化浮点数：将尾数的绝对值限定在区间[0.5,1]。
广泛采用的标准是IEEE 754。

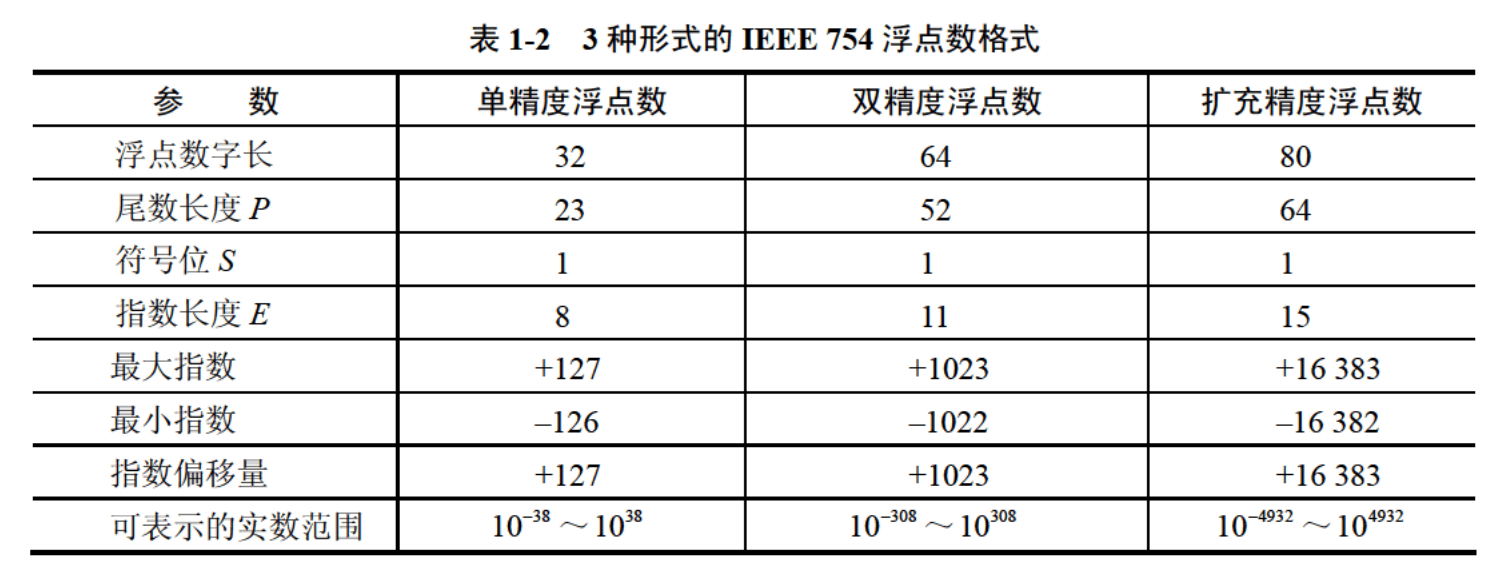
根据IEEE 754，被编码的值分为3种情况：规格化的值、非规格化的值和特殊值。

规格化的值：阶码部分的二进制值不全为0也不全为1。
非规格化的值：阶码部分的二进制全为0。
特殊值：阶码部分的二进制值全为1。

这三种状态也是人为定义。根据运算结果的二进制表示，人为分类的。

软件设计师教程例题：利用IEEE 754标准将176.0625表示为单精度浮点数

十进制转换为二进制： $176.0625)_{10}=(1011 0000.0001)_2$
规格化处理： $1011\ 0000.0001=1\diamondsuit 011\ 0000\ 0001\times2^7$
满足 $b_0=1$ ，而且小数点在 $\diamondsuit$ 的位置上，去掉 $b_0$ 并扩展为单精度浮点数规定的23位尾数：

$011\ 0000\ 0001\ 0000\ 0000\ 0000$

求阶码：规格化处理得到的阶码为7，单精度浮点数规定的指数偏移量为127，不是前面移码的128。那么阶码E=7+127=134。

$134)_{10}=(1000\ 0110)_2$

最后，可以得到 $176.0625)_{10}$ 的单精度浮点数表示：

单精度浮点数转真值
呈上学校ppt的例题：

浮点数运算

以下来自软件设计师教程

设有浮点数 $X=M\times2^i,Y=N\times2^j$ ：

对阶：小数向大数对齐，阶码小的数尾数右移k位，阶码加上k，k=|i-j|。
求尾数和。
结果规格化并判溢出：如果结果不是规格化的数，则需要规格化；如果溢出，则需要调整阶码。
舍入处理：对结果右规、对阶过程中会因尾数右移而使最低为丢掉。
溢出判别：以阶码为准，若阶码溢出，则运算结果溢出；若结果下溢，小于最小值，则结果为0。

浮点数乘法：积的阶码等于两乘数的阶码相加，积的尾数等于两乘数的尾数相乘。
浮点数除法：商的阶码等于两数的阶码相减，商的尾数等于两数的尾数相除。
乘除运算的结果都需要进行规格化处理并判断阶码是否溢出。

阶码与规格化

到这里还没提规格化的方式。
规格化发生在尾数运算结束后，我们需要使其“符合约定”，也就是一开始提到的，尾数第一位默认为1。
尾数运算结果需要规格化的情况有两种：

10.01：小数点不在 $b_0$ 之后，需要右移，尾数边小了，阶码需要+1变大。
0.1001： $b_0\neq1$ ，需要左移，尾数变大了，阶码需要-1变小。

也就是说，在尾数位移的过程中，可以会丢失最低位，影响数值精度。
在对阶过程中，阶码可能会小于0，也可能会溢出。

非规格化的值

如果对阶后阶码等于0000 0000。
这也就对应“非规格化的值”，由于阶码是由移码表示的，因此0x00在移码中表示最小的数。如果指数非常小，那么最后的结果将趋近于0。
也因此，非规格化的值往往用于表示：0或非常接近0的数。

特殊值

如果对阶后阶码等于1111 1111，在移码中表示最大的数。
当尾数部分全为0时，说明产生了溢出，将表示无穷大。
由于符号位单独存储，占用一位，因此存在正零和负零两种情况
如果尾数部分不全为0，将表示为“NaN”不是一个数。
“非规格化值”和“特殊值”也是对二进制数的人为定义。
就跟3.1415...起名为pi一样，你也可以人为地定义成你喜欢的名字。
因此，上述的加减法过程可以简化为：

对阶
求尾数和
规格化

对于舍入和溢出判别，这是对浮点数的二进制特殊形式的人为定义。

浮点数的表示范围

浮点数阶码用移码，二进制表示越大，其真值越大。
尾数是直接翻译成二进制，二进制越大，真值越大。
有单独的符号位表示正负，浮点数在正数和负数所表示的范围应当是对称的。

因此浮点数的范围可以通过对阶码和尾数全部置1或置0来猜测其表示范围的上下界。

当阶码除最后一位全部置1时，移码表示的数最大，为： $2^{2^8-2-127}=2^{127}$
当阶码除最后一位全部置0时，移码表示的数最小，为： $2^{1-127}=2^{-126}$
下式中第一个1为浮点数中约定省略的，小数点前的1，在存储时隐去，计算时补回：

如果尾数全部置1，则尾数表示的数最大，为： $1+2^{-1}+2^{-2}...2^{-23}==1+1-2^{-23}=2-2^{-23}$
如果尾数除全部置0，尾数表示的数最小，为： $1$

32位单精度浮点数表示的范围可以归纳成：

阶码全部置1和置零为人为定义的两种特殊情况：

全部置1：无穷大或“NaN”
全部置0：0或非常接近0的数

由于单精度浮点数只有32位，如果是按照补码或移码的偏移方式，能表示 $2^{32}$ 个数字。而由于浮点数范围比定点数大，但数的个数没变多，故数之间更稀疏，且不均匀。

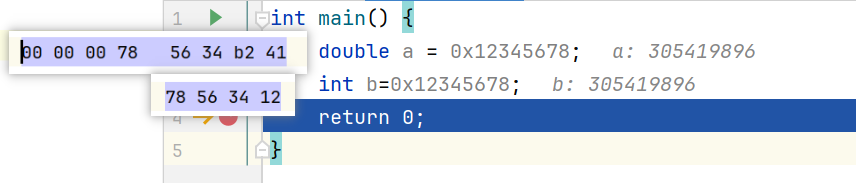
C语言中的浮点数

如果你稍微学过，你应该知道，C语言浮点数是不能直接用等号判断的。

double a = 1.1;
double b = 1.2 - 0.1;
//1.100000        1.100000        0
printf("%lf\t%lf\t%d", a, b, a == b);

尽管输出都是1.100000，但最后比较的结果仍然是0。
正确的比较方式应该使用fabs()对浮点数做差之后的结果取绝对值，与定义好的精度比较。
比如：fabs(a-b)<0.0001，只要a-b做差后的结果的绝对值小于0.0001，那么就可以看作是相等。

这里稍微不好理解的就是①和②。
不相等的的原因是，int和float都是32位，表示的数字数量是相等的，但范围不对等。两次类型转换可能会损失数据。
至于具体的存储方式，等我文化水平再高一点，再说。

总结

已知8位二进制数，计数周期为256，计数周期的一半为128。
求补码： $[X]_补=\left\{ \begin{aligned} &X\quad X>=0\\ &X+256 \quad X<0 \end{aligned}\right.$
求移码： $X]_移=X+128$
原码和反码没啥用。
单精度浮点数表示： $1_{符号位S}+8_{阶码E}+23_{尾数M}$

阶码用移码，偏移量为127，指数位置，决定数值范围。
尾数是纯二进制，有说原码也有说补码，系数位置，决定数值精度。

真值求浮点数的时候默认小数点前有个1，会隐去。
浮点数求真值的时候要把小数点前的1加回来。
浮点数运算：小数向大数对阶，尾数相加，规格化。

胡扯几句

其实到这里就已经足够了。

人为规定&偏移量

单纯对01串提偏移量可能比较抽象。
一个形象的偏移方式就是“凯撒密码”：对字符串添加+3的偏移量，使得原文ABC表示为密文DEF。
这里的+3偏移量也是凯撒人为定义的。此时添加偏移量是为了加密。
跟码制相关的偏移方法的话，有余三码和ASCII码。
余三码就是对数字0~9添加一个+3的偏移量，即： $[X]_{余三}=X+3\quad 0\leq X\leq9$
在对余三码进行加法运算时，相当于加了两次3，因此结果需要减掉一个3。
如果产生进位的话，结尾0对应的二进制表示应该是11，结果需要加上一个3。
根据我脑子里残留的数电知识，此时添加偏移量是为了减少零一变换的频率，以降低数据的出错率。
这里需要搞清楚进位和溢出，尽管我也会经常说错：

溢出：有符号数的溢出
进位：无符号数的溢出

ASCII码就是对数字0~9添加一个+48的偏移量，即： $[X]_{ASCII}=X+48\quad 0\leq X\leq9$
char类型值48如果用%c的转换规范，那么结果是对应的ASCII码0，如果是%uud，那么结果是补码48。
无论是0还是48，都是人为定义。你也可以自己实现一个函数，输入48的时候，输出自定义的字符串。

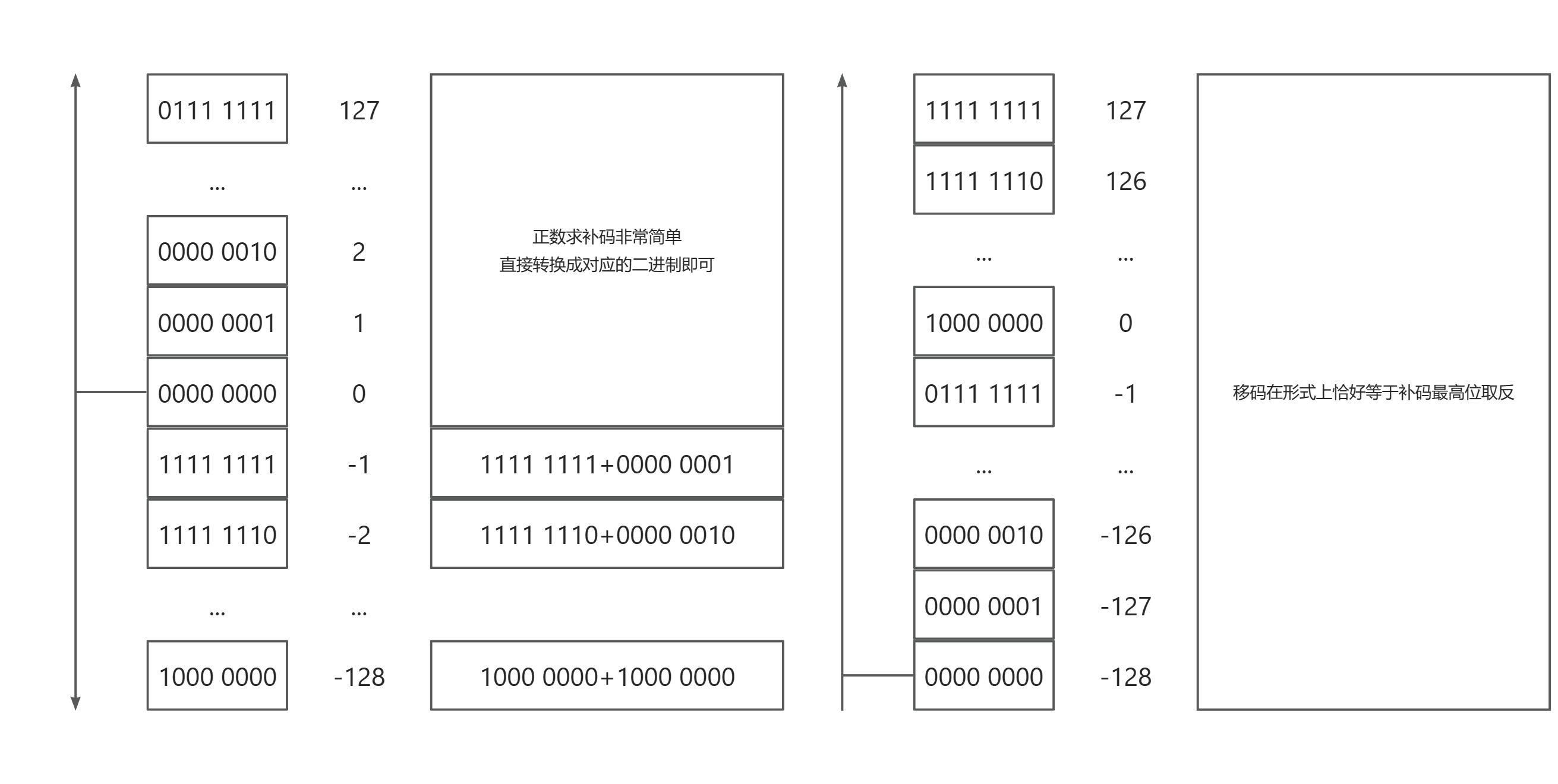
对于8位二进制，我们需要划分一部分表示正数，划分一部分表示负数，理想化的方法就是正数负数各占一半。
至于二进制与十进制有符号数的对应关系，需要我们人为定义。这就需要对一部分数据添加一个偏移量。
比如在补码中：

0x00到0x7f表示的二进制数与实际需求相同，不作偏移。
0x80到0xff表示-128到-1，需要将二进制对应的十进制加上一个人为规定的偏移量-256。

在移码中：

0x00到0xff表示-128到127，需要将二进制对应的十进制加上一个人为规定的偏移量128。

在上面的余三码中，需要根据是否进位，对计算后的结果再修改一次。
而在补码和移码中，不需要这一步，运算的结果就是最终结果：

补码的偏移量256，刚好是进位，无论加减，不影响结果。
移码只涉及比较和减法运算，只需要能表达差值即可。加法的时候不会用到移码。

虽然说浮点数的阶码用的是移码，但单精度浮点数规定的偏移量是127，而不是128。

面向硬件编程

以char类型的变量a为载体举个例子：

char a = 255;
//-1      ff
printf("%hhd\t%hhx", a, a);
a += 1;
//0     0
printf("%hhd\t%hhx", a, a);
unsigned char b = -1;
//255    ff
printf("%hhu\t%hhx", b, b);

char类型的数值范围应该是-128-127。但将255赋值给a，是不会报错的。甚至255+1也不会报任何错误。
unsigned char类型应该只有正数，但用负数赋值的时候并没有报错，还能正常输出255。
如果你接触过面向硬件编程，那么你应该知道，无论是char还是int，都只是申请了一段内存空间，区别在于内存空间的大小和默认的转换规范不同。比如51单片机通常直接用unsigned char或者unsigned int申请8位或16位空间，申请过来是为了方便操作寄存器，而不完全是为了计算。
将255赋值给a输出的结果和-1相同，原因是它们对应的二进制表示是相同的，都是1111 1111，通过char类型的转换规范，输出的结果就是-1，如果是unsigned char，那么结果将是255。

小记

之前写过一篇博客（http://t.csdnimg.cn/SW5yc），内容是原码反码补码的内容。
当时是在学“数字逻辑”，在别的学校应该叫“数电”。
当时我文化水平不够，很快就有大佬发现了问题，这是他的博客专栏（http://t.csdnimg.cn/1522w）我觉得他讲的很好。
这学期的计组又要学这玩意，现在回顾梳理一下。
东西有点多，这篇博客还是有点乱，中间可能会反复修改几次。
现在文化水平还是不够，可能还存在问题，欢迎评论区或私聊指正。