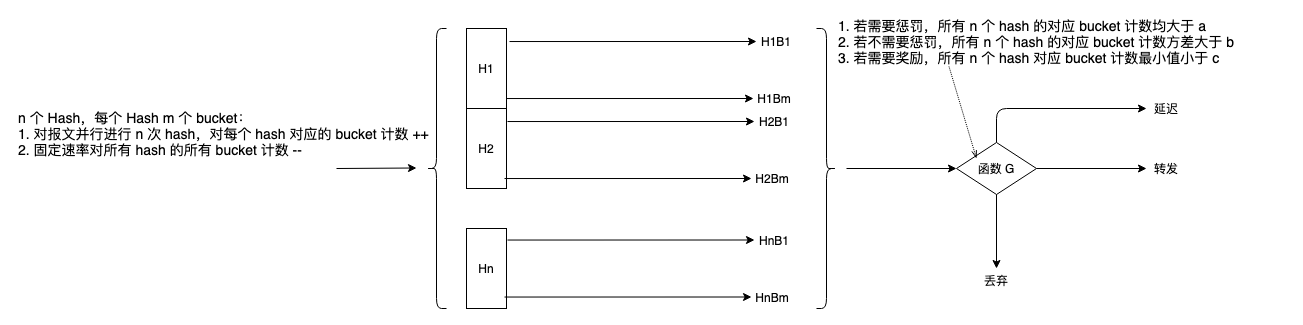
多叉树

在二叉树中每个结点只能有一个数据项, 并且最多有两个子节点, 如果允许每个结点可以有更多的数据项和更多的子节点, 那么就是多叉树

• 多叉树: multiway tree

那么我们为什么要提出多叉树?

因为二叉树有一定的问题: 即使二叉树的操作效率高, 但是也存在问题: 二叉树需要加载的内存的时候, 如果二叉树的结点少, 那么没有什么问题, 但是如果二叉树的结点有很多(比如: 有一亿个结点), 就存在如下问题:

1. 在构建二叉树时, 如果构建二叉树的数据是从文档中或者从数据库(DB)中加载的, 那么海量的结点, 构建二叉树时的速度就会很慢
2. 如果结点很多, 也会造成二叉树的高度很大, 操作的效率就会降低, 因为树结构的操作效率和树的高度是息息相关的
   • 在数据库查询中, 以树存储数据, 树有多少层, 就意味着要读多少次磁盘I/O
     • 所以树的高度越低, 就意味着查询数据时, 需要读IO的次数就越少(众所周知, 读IO时候一件费时的操作)
     • 因为我们查询的时候查询的次数就是树的高度次数, 所以树的高度就决定了要和多少次IO

后面我们讲解的2-3树, 2-3-4树就是多叉树, 多叉树通过重新组织结点, 减少树的高度, 能对二叉树进行优化

2-3树举例:

我们将上面中结点有两个数据项的结点称之为: “3结点”, 将上面结点中只有一个数据项的结点称之为:“2结点”

• 2-3树就是由2结点和3结点构成的树

2-3树和2-3-4树都是B树的一种, 我们后面在讲B树的时候会专门对2-3树进行讲解

• 2-3树是最简单的B树

• 对于2-3树中的"2结点"来讲: 其要么是没有子节点, 要么是有两个子节点

• 对于2-3树中的"3结点"来讲: 其要么是没有子节点, 要么是有三个子节点

• 对于"2结点"和"3结点"没有子节点的时候就是做叶子结点的时候

2-3树其实就是一个三阶B树, 2-3-4树其实就是一个四阶B树

单词积累:

multiway : 多路的

• multiway tree 多叉树