1.并查集原理
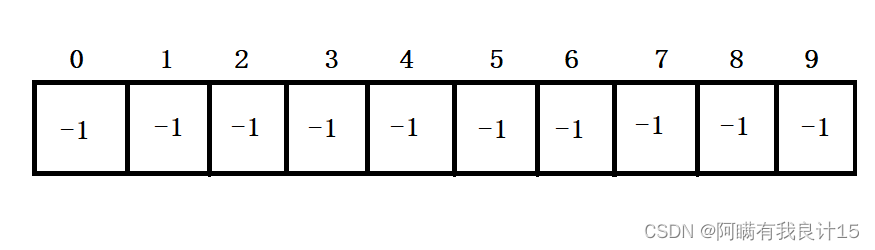
某公司今年校招全国总共招生10人,西安招4人,成都招3人,武汉招3人,10个人来自不同的学校,起先互不相识,每个学生都是一个独立的小团体,现给这些学生进行编号:{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体,数组中的数字代表:该小集体中具有成员的个数。
毕业后,学生们要去公司上班,每个地方的学生自发组织成小分队一起上路,于是:
西安学生小分队s1={0,6,7,8},成都学生小分队s2={1,4,9},武汉学生小分队s3={2,3,5}就相互认识了,10个人形成了三个小团体。假设有三个群主0,1,2担任队长,负责大家的出行。
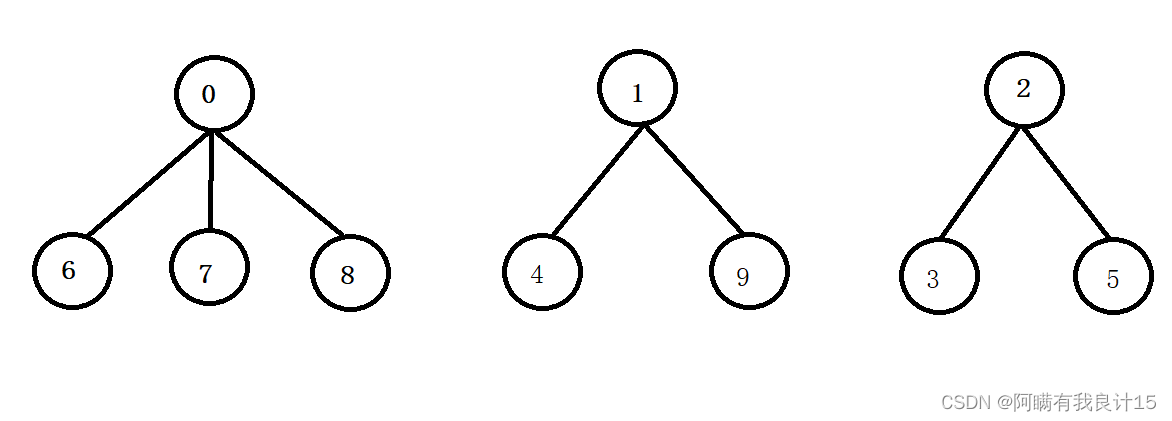
一趟火车之旅后,每个小分队成员就互相熟悉,成为了一个朋友圈。
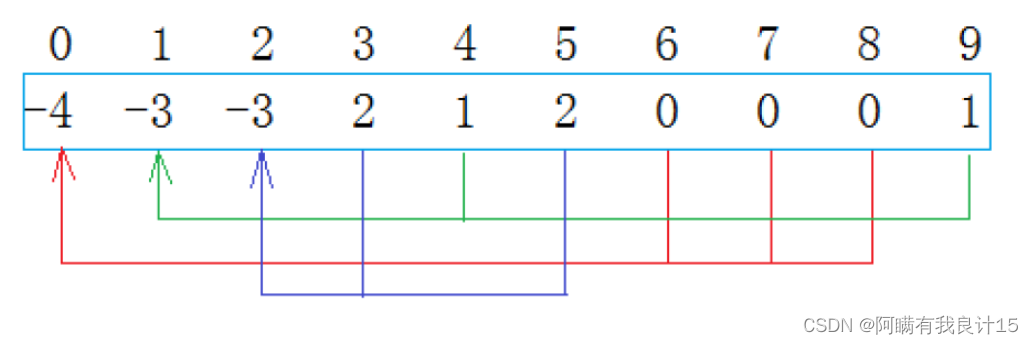
从上图可以看出:编号6,7,8同学属于0号小分队,该小分队中有4人(包含队长0);编号为4和9的同学属于1号小分队,该小分队有3人(包含队长1),编号为3和5的同学属于2号小分队,该小分队有3个人(包含队长1)。
- 数组的下标对应集合中元素的编号
- 数组中如果为负数,负号代表根,数字代表该集合中元素个数
- 数组中如果为非负数,代表该元素双亲在数组中的下标
在公司工作一段时间后,西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起,两个小圈子的学生相互介绍,最后成为了一个小圈子:
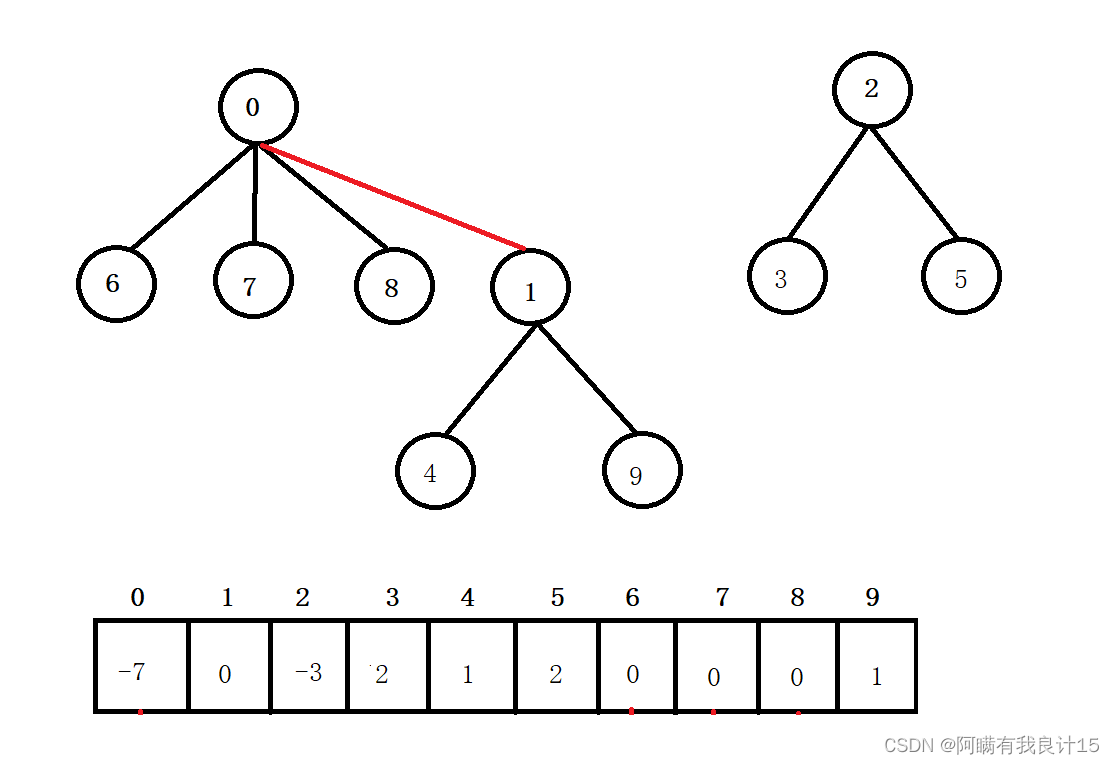
通过以上例子可知,并查集一般可以解决一下问题:
1.查找元素属于哪个集合
沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置)
2.查看两个元素是否属于同一个集合沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
3.将两个集合归并成一个集合将两个集合中的元素合并,将一个集合名称改成另一个集合的名称
4.集合的个数
2.并查集实现
package test;
import java.util.Arrays;
public class UnionFindSet {
public int[] elem;
public int usedsize;
public UnionFindSet(int n) {
this.elem = new int[n];
Arrays.fill(elem, -1);
}
//查询x的根节点
public int findRoot(int x) {
if (x < 0) {
throw new IndexOutOfBoundsException("下标不合法,是负数");
}
while (elem[x] >= 0) {
x = elem[x];
}
return x;
}
//查询x y 是不是同一个集合
public boolean isSameUnionFindSet(int x, int y) {
int index1 = findRoot(x);
int index2 = findRoot(y);
if (index1 == index2) {
return true;
}
return false;
}
//合并
public void union(int x, int y) {
int index1 = findRoot(x);
int index2 = findRoot(y);
if (index1 == index2) {
return;
}
elem[index1] = elem[index1] + elem[index2];
elem[index2] = index1;
}
//集合的个数
public int getCount() {
int count = 0;
for (int x : elem) {
if (x < 0) {
count++;
}
}
return count;
}
public void print() {
for (int x : elem) {
System.out.print(x + " ");
}
System.out.println();
}
public static void main(String[] args) {
UnionFindSet unionFindSet = new UnionFindSet(10);
unionFindSet.union(0, 6);
unionFindSet.union(0, 7);
unionFindSet.union(0, 8);
unionFindSet.union(1, 4);
unionFindSet.union(1, 9);
unionFindSet.union(2, 3);
unionFindSet.union(2, 5);
unionFindSet.union(8, 1);
unionFindSet.print();
System.out.println("查找是不是同一个集合");
System.out.println(unionFindSet.isSameUnionFindSet(6, 9));
System.out.println(unionFindSet.isSameUnionFindSet(8, 2));
}
}
3.例题
1.家族

package test;
import java.util.Arrays;
public class UnionFindSet {
public int[] elem;
public int usedsize;
public UnionFindSet(int n) {
this.elem = new int[n];
Arrays.fill(elem, -1);
}
//查询x的根节点
public int findRoot(int x) {
if (x < 0) {
throw new IndexOutOfBoundsException("下标不合法,是负数");
}
while (elem[x] >= 0) {
x = elem[x];
}
return x;
}
//查询x y 是不是同一个集合
public boolean isSameUnionFindSet(int x, int y) {
int index1 = findRoot(x);
int index2 = findRoot(y);
if (index1 == index2) {
return true;
}
return false;
}
//合并
public void union(int x, int y) {
int index1 = findRoot(x);
int index2 = findRoot(y);
if (index1 == index2) {
return;
}
elem[index1] = elem[index1] + elem[index2];
elem[index2] = index1;
}
//
public int getCount() {
int count = 0;
for (int x : elem) {
if (x < 0) {
count++;
}
}
return count;
}
public void print() {
for (int x : elem) {
System.out.print(x + " ");
}
System.out.println();
}
public static void main(String[] args) {
UnionFindSet unionFindSet = new UnionFindSet(10);
unionFindSet.union(0, 6);
unionFindSet.union(0, 1);
unionFindSet.union(3, 7);
unionFindSet.union(4, 8);
System.out.println("以下是不是亲戚?");
boolean flg = unionFindSet.isSameUnionFindSet(1, 6);
if (flg) {
System.out.println("是亲戚");
} else {
System.out.println("不是亲戚");
}
}
}
2.省份数量

class UnionFindSet {
public int[] elem;
public int usedsize;
public UnionFindSet(int n) {
this.elem = new int[n];
Arrays.fill(elem, -1);
}
//查询x的根节点
public int findRoot(int x) {
if (x < 0) {
throw new IndexOutOfBoundsException("下标不合法,是负数");
}
while (elem[x] >= 0) {
x = elem[x];
}
return x;
}
//查询x y 是不是同一个集合
public boolean isSameUnionFindSet(int x, int y) {
int index1 = findRoot(x);
int index2 = findRoot(y);
if (index1 == index2) {
return true;
}
return false;
}
//合并
public void union(int x, int y) {
int index1 = findRoot(x);
int index2 = findRoot(y);
if (index1 == index2) {
return;
}
elem[index1] = elem[index1] + elem[index2];
elem[index2] = index1;
}
//
public int getCount() {
int count = 0;
for (int x : elem) {
if (x < 0) {
count++;
}
}
return count;
}
public void print() {
for (int x : elem) {
System.out.print(x + " ");
}
System.out.println();
}
}
class Solution {
public int findCircleNum(int[][] isConnected) {
int n = isConnected.length;
UnionFindSet unionFindSet = new UnionFindSet(n);
for (int i = 0; i < isConnected.length; i++) {
for (int j = 0; j < isConnected[0].length; j++) {
if (isConnected[i][j] == 1) {
unionFindSet.union(i, j);
}
}
}
return unionFindSet.getCount();
}
}3.等式方程的可满足性

class UnionFindSet {
public int[] elem;
public int usedsize;
public UnionFindSet(int n) {
this.elem = new int[n];
Arrays.fill(elem, -1);
}
//查询x的根节点
public int findRoot(int x) {
if (x < 0) {
throw new IndexOutOfBoundsException("下标不合法,是负数");
}
while (elem[x] >= 0) {
x = elem[x];
}
return x;
}
//查询x y 是不是同一个集合
public boolean isSameUnionFindSet(int x, int y) {
int index1 = findRoot(x);
int index2 = findRoot(y);
if (index1 == index2) {
return true;
}
return false;
}
//合并
public void union(int x, int y) {
int index1 = findRoot(x);
int index2 = findRoot(y);
if (index1 == index2) {
return;
}
elem[index1] = elem[index1] + elem[index2];
elem[index2] = index1;
}
//
public int getCount() {
int count = 0;
for (int x : elem) {
if (x < 0) {
count++;
}
}
return count;
}
public void print() {
for (int x : elem) {
System.out.print(x + " ");
}
System.out.println();
}
}
class Solution {
public boolean equationsPossible(String[] equations) {
UnionFindSet unionFindSet = new UnionFindSet(26);
for (int i = 0; i < equations.length; i++) {
if (equations[i].charAt(1) == '=') {
unionFindSet.union(equations[i].charAt(0) - 'a', equations[i].charAt(3) - 'a');
}
}
for (int i = 0; i < equations.length; i++) {
if (equations[i].charAt(1) == '!') {
int index1 = unionFindSet.findRoot(equations[i].charAt(0) - 'a');
int index2 = unionFindSet.findRoot(equations[i].charAt(3) - 'a');
if (index1 == index2) {
return false;
}
}
}
return true;
}
}





![B+树 [数据结构与算法][Java]](https://img-blog.csdnimg.cn/aca3791fc1f04d0c9864886dc620b22f.png#pic_center)