文章目录
- 用队列实现栈
- 用栈实现队列
- 设计循环队列
用队列实现栈
链接:用队列实现栈

这道题是让我们用两个队列实现一个栈,简单来说,就是利用队列来实现一个先入后出的功能,我们知道队列是先入先出,如何用两个队列来实现后入先出呢?比如说,
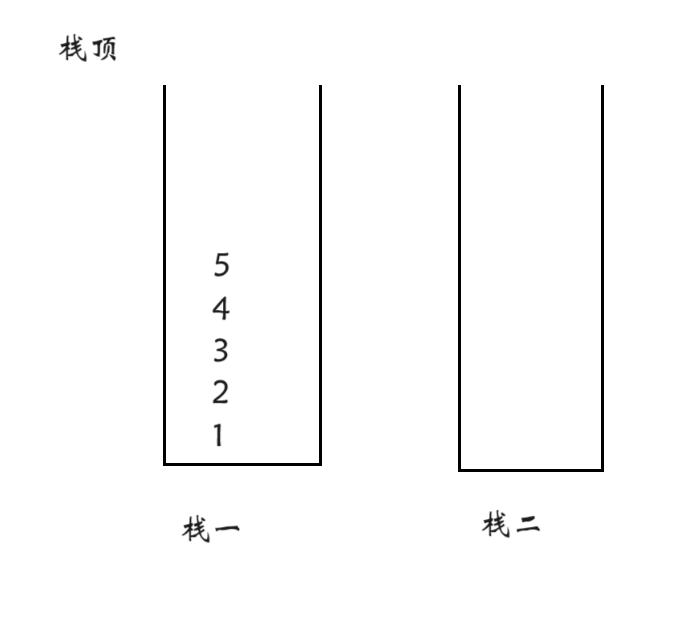
我们现在有五个数据进入了第一个队列
之后我们如果要按照栈的形式取出数据的话,要取出5,只靠队列一肯定是不行了,要把前四个数据挪到队列二,再把五取出来就可以了
这时取出4还是一样的操作,挪动在取出。如果要插入呢?肯定要插在4的后面,不知道你有没有发现,两个队列总是一个为空,另一个可能空(刚开始什么数据都没有),也可能不空。
总结:插入的话就插入非空的队列,取出的话就是先挪动在取出。
typedef struct {
Que queue1;
Que queue2;
} MyStack;
MyStack* myStackCreate() {
MyStack*obj=(MyStack*)malloc(sizeof(MyStack));
QueueInit(&obj->queue1);
QueueInit(&obj->queue2);
return obj;
}
void myStackPush(MyStack* obj, int x) {
if(!QueueEmpty(&obj->queue1)){
QueuePush(&obj->queue1,x);
}
else{
QueuePush(&obj->queue2,x);
}
}
int myStackTop(MyStack* obj) {
if(!QueueEmpty(&obj->queue1)){
return QueueBack(&obj->queue1);
}
else{
return QueueBack(&obj->queue2);
}
}
int myStackPop(MyStack* obj) {
Que* Empty=&obj->queue1;
Que* UnEmpty=&obj->queue2;
if(!QueueEmpty(&obj->queue1)){
Empty=&obj->queue2;
UnEmpty=&obj->queue1;
}
while(QueueSize(UnEmpty)>1){
QDataType tmp= QueueFront(UnEmpty);
QueuePop(UnEmpty);
QueuePush(Empty,tmp);
}
QDataType tmp= QueueFront(UnEmpty);
QueuePop(UnEmpty);
return tmp;
}
bool myStackEmpty(MyStack* obj) {
return QueueEmpty(&obj->queue1)&&QueueEmpty(&obj->queue2);
}
void myStackFree(MyStack* obj) {
QueueDestroy(&obj->queue1);
QueueDestroy(&obj->queue2);
free(obj);
}
这里只有实现的栈的函数代码,当然我们需要把自己实现的队列的代码粘贴到题中,也可以看我的另外一篇博客,那里面有源码
链接:栈和队列
用栈实现队列
链接:用栈实现队列

这个跟上个题非常的类似,要求都是一样的,就是实现的思想不太一样,栈是要求后进先出,我们如何用两个栈实现先入先出呢?比如说:
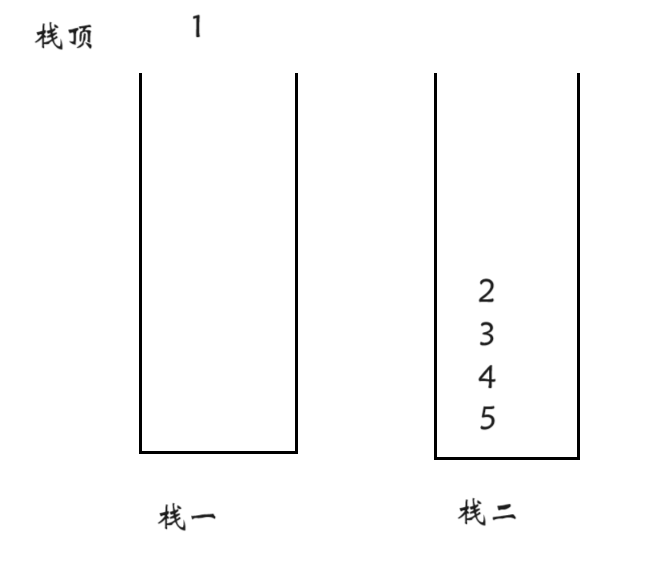
我们先给一个栈中放上五个数据
我们现在要取出栈一当中的1,无可厚非,也是倒数据嘛对不对,先把2,3,4,5倒到栈二,再把一取出就可以了。
如果现在我们要取出2呢?好像这次不用倒了,直接取就行。我要插入数据呢?得插到栈一,因为插到栈二数据就乱了,栈二的数据取出完了就把栈一的数据倒到栈二,依次类推,就可以得到一个队列了。不知道你有没有发现,栈一只需要插入数据,栈二只需要取出数据。
总结:一个栈负责插入数据,一个栈负责出数据,出数据的栈没了数据就从插入数据的栈中倒过来。
typedef struct {
ST push;
ST pop;
} MyQueue;
MyQueue* myQueueCreate() {
MyQueue*tmp=(MyQueue*)malloc(sizeof(MyQueue));
STInit(&tmp->push);
STInit(&tmp->pop);
return tmp;
}
void myQueuePush(MyQueue* obj, int x) {
STPush(&obj->push,x);
}
int myQueuePeek(MyQueue* obj) {
if(!STEmpty(&obj->pop)){
return STTop(&obj->pop);
}
while(!STEmpty(&obj->push)){//倒数据
STDataType tmp=STTop(&obj->push);
STPop(&obj->push);
STPush(&obj->pop,tmp);
}
return STTop(&obj->pop);
}
int myQueuePop(MyQueue* obj) {
myQueuePeek(obj);
STDataType tmp=STTop(&obj->pop);
STPop(&obj->pop);
return tmp;
}
bool myQueueEmpty(MyQueue* obj) {
return STEmpty(&obj->pop)&&STEmpty(&obj->push);
}
void myQueueFree(MyQueue* obj) {
STDestroy(&obj->pop);
STDestroy(&obj->push);
free(obj);
}
同理,这个也是需要栈的代码的,链接在上面
设计循环队列
链接:设计循环队列

什么叫循环队列呢?就是说一个队列的长度是一定的,只要有空间我们要一直从尾插入,头出,即使这个尾在头的前面。这个循环队列用数组来实现是非常理想的,我们还可以多开辟一个空间来区分空和满。
我们还是画图来解释一下
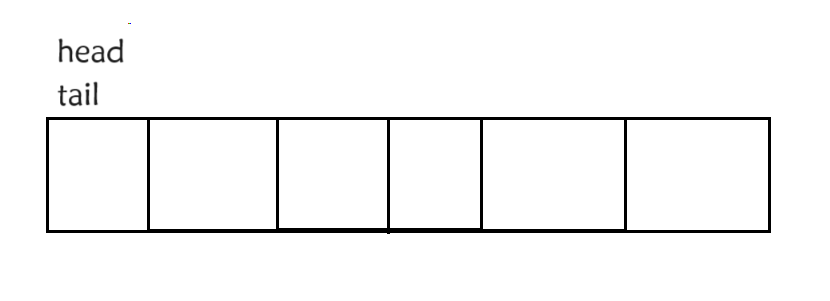
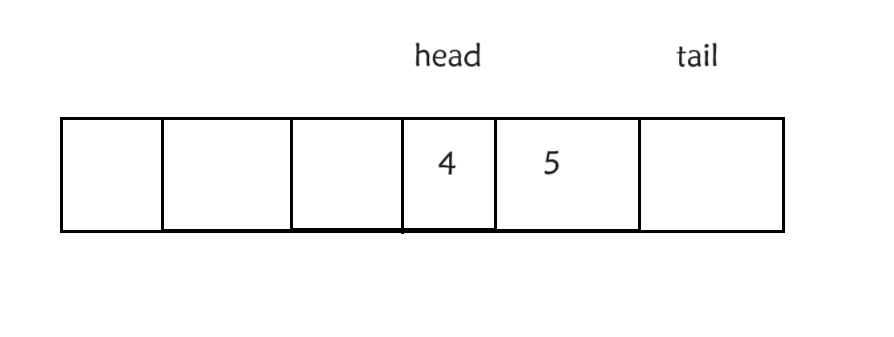
比如说我们开辟一个六个空间的数组,一开始头和尾都在开头位置,我们要插入的话要在tail的位置插入,并且tail要走向后一个
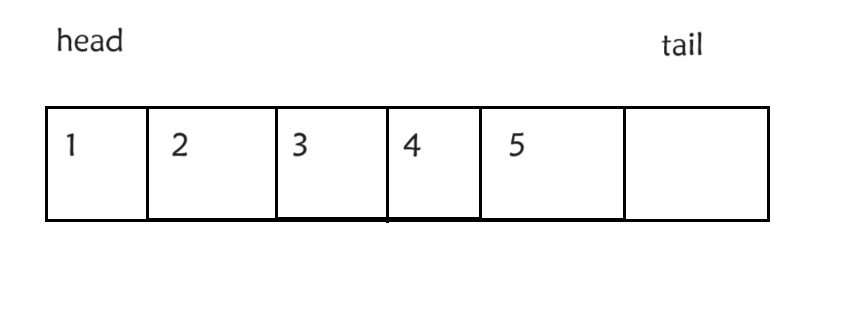
比如说我们插入五个数据,这时就满了,因为我们如果要插入6个数据的话,空和满不能区分,head都是等于tail,但现在tail的下一个为head就证明满了,如果要出的话也简单
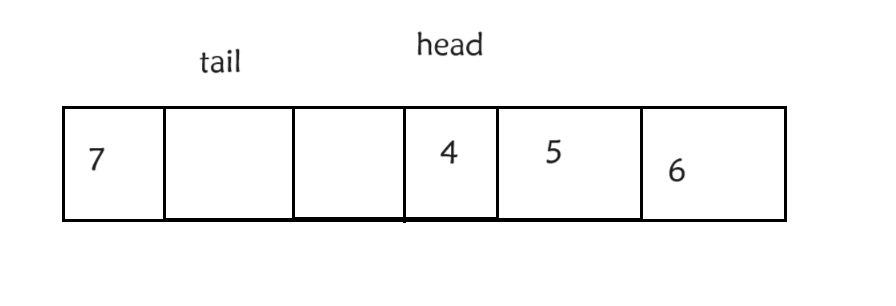
这是再插入就要在返回数组的前边插入了,具体代码实现就是取余
这样就实现了循环功能
typedef struct {
int*a ;
int head;
int tail;
int size;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue*tmp=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
tmp->a=(int*)malloc(sizeof(int)*(k+1));
tmp->head=0;
tmp->tail=0;
tmp->size=k+1;
return tmp;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if((obj->tail+1)%obj->size==obj->head){
return false;
}
else{
obj->a[obj->tail]=value;
obj->tail=(obj->tail+1)%(obj->size);
return true;
}
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(obj->head==obj->tail){
return false;
}
else{
obj->head=(obj->head+1)%(obj->size);
return true;
}
}
int myCircularQueueFront(MyCircularQueue* obj) {
if(obj->head==obj->tail){
return -1;
}
else{
return obj->a[obj->head];
}
}
int myCircularQueueRear(MyCircularQueue* obj) {
if(obj->head==obj->tail){
return -1;
}
else{
return obj->a[(obj->tail+obj->size-1)%obj->size];
}
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->head==obj->tail;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->tail+1)%obj->size==obj->head;
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
free(obj);
}
中间有很多的取余操作,目的就是找到逻辑上的下一个位置,但在物理上它确实是在前面。