对于任何对数学和科学感兴趣的人，您可能已经知道了急速线，因为它经常在各种流行的教学频道（例如 Vsauce 和 3Blue1Brown）上谈论。虽然有多种方法可以解决急速线问题，但在这篇文章中，本文将使用变分法来推导急速线的方程。

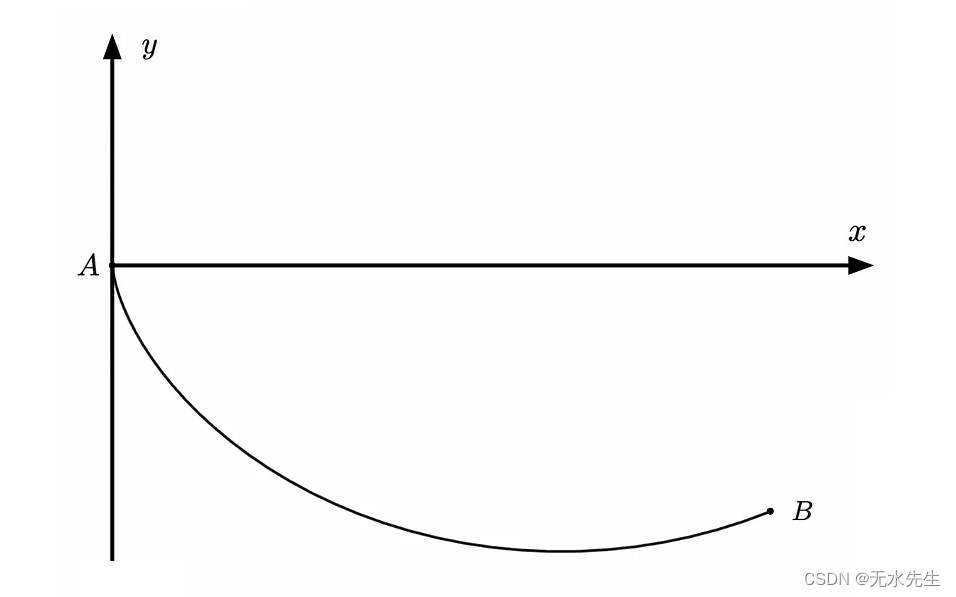
        现在，在继续之前，如果有些人不知道什么是急速线，请考虑在空间中有两个点（具有不同的水平和垂直位置），并用一些任意曲线连接这两个点，如下所示。

        如果我们让一个球从 A 点滚动，在大多数情况下，它会在一段时间后到达 B 点（假设没有摩擦或空气阻力）。那么问题是，什么曲线形状可以最小化下降时间？虽然人们可能会猜测它只是一条直线，但这根本不正确，事实证明实际形状是我上面已经显示的形状。这就是所谓的“brachistochrone”曲线（来自希腊语“brachistos”和“chronos”，分别表示“最短”和“时间”）。

二、降临之时

        现在我们已经定义了速时线是什么，我们可以尝试推导出代表它的方程。为此，我将使用变分法，这是解决这个问题的自然方法，因为它是一个关于寻找最小化函数的路径的问题。如果你对变分法不太熟悉，可以看看我之前写的这篇文章。

        第一步涉及找到球从A点到B点所需时间的表达式（我现在将其称为 τ），这 可以通过简单地采用以下积分来完成：τ = ∫ dt。然而，这并没有真正帮助我们，因为我们的积分需要我们根本不知道的界限。我们可以做的是利用速度方程v = ds / dt重写这个表达式。重新排列它并将其替换为dt将为我们提供下降时间的新表达式：τ = ∫ ds / v。

        虽然我们还不能用这个表达式做任何事情，但我们可以以更方便的方式重写各个术语。从ds项开始，可以使用ds² = dx² + dy²重写。此外，由于x ' = dx / dy我们可以使用ds² = ( x' ² + 1) dy ²。现在，转向速度，我们可以利用能量守恒定律来推导出这个表达式。由于我们是从高点（从静止状态）落下球，因此它的重力势能mg Δ h将转换为动能 1/2 mv ²。如果我们使用下面所示的轴，则曲线上某个点的高度变化 Δ h将是 - y，您可以确认。因此，如果我们替换它并重新排列，我们得到以下速度方程：v ² = -2 gy（请注意，由于曲线位于x轴下方，因此y始终为负值，因此 -2 gy将为正值，即使v真实，因为它应该是）。

        将所有这些信息放在一起，我们将以以下表达式结束从A点到B点所需的时间：

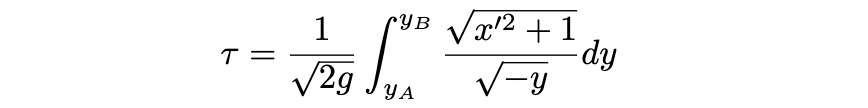
三、推导急速线

        有了这个下降时间的表达式，我们现在可以使用变分法来找到使时间最小化的路径。正如您在上面的表达式中所看到的，我们正在尝试找到一条路径x ( y )，它可以最小化积分的值，这正是我们在变分法中所做的。因此，我们能做的就是使用欧拉-拉格朗日方程，其中函数f是上述积分的被积函数：

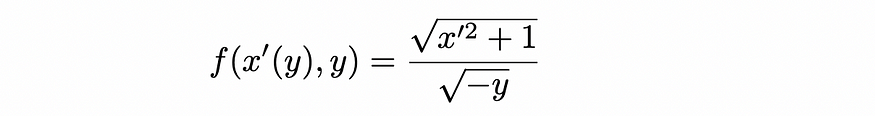
        将其代入欧拉-拉格朗日方程得出：

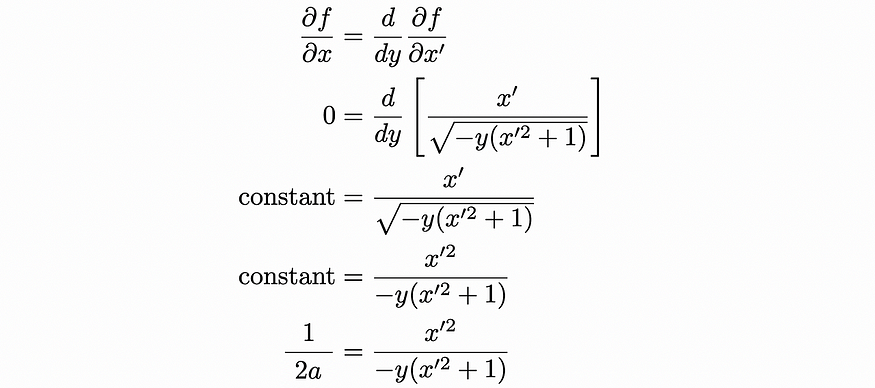
        在第三行中，为了方便起见，我对两边都进行了平方，在最后一行中，我将常数命名为 1/2 a，稍后会用到。然后可以重新排列以获得x'的方程：

        我们现在可以将其与y积分以找到x的表达式。然而，我们需要求解的积分实际上并不那么明显，我们必须使用以下替换来求解：y = -a (1 - cos θ )。这将给出dy = - a sin θ dθ，我们现在可以用它来求解积分：

        （假设我们从原点开始，积分常数将为 0）。虽然从技术上讲我们还没有导出表示曲线的单个函数（例如y ( x ) 或x ( y )），但我们的工作实际上已经完成，因为我们有两个x和y参数方程，如下所示：

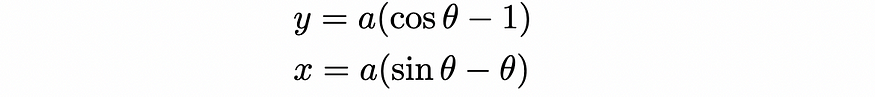
        如果我们愿意的话，我们实际上可以继续绘制这些参数方程，看看曲线是什么样的（我使用的是 Desmos，但任何其他支持参数方程的图形计算器都可以）：

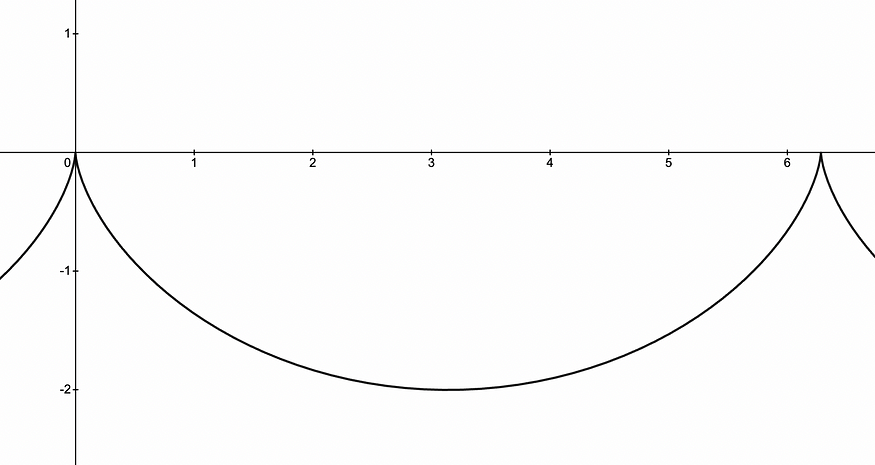
        上面显示的曲线正是我们正在寻找的急速曲线，其形状就是所谓的“摆线”。摆线是在轮子边缘标记一个点并在轮子沿x轴滚动时沿着该点描绘的路径创建的形状（如果搜索“摆线”，您可能会找到动画描述了这一点）。正如我之前展示的，两点之间下降最快的曲线只是该摆线形状的一部分。虽然沿着曲线滚动的球与水平滚动的轮子有任何关系确实很奇怪，但我们通过使用变分法成功地确认了摆线确实是急速曲线。但是，如果您想要以更直观的方式了解急速线和摆线之间的关系，我强烈建议您查看3Blue1Brown 的视频，因为他采用了与我在本文中完全不同的方法。

        感谢您的阅读。

四、参考

     泰勒，JR（2005）。经典力学。大学科学书籍。