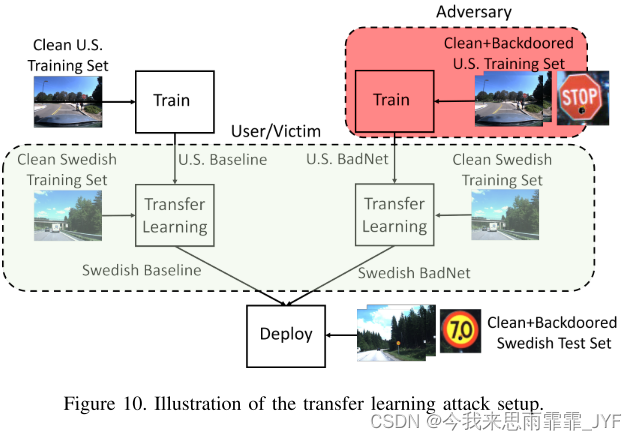
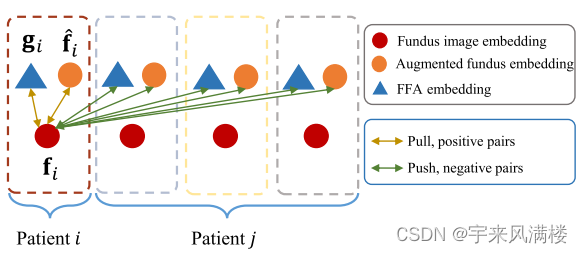
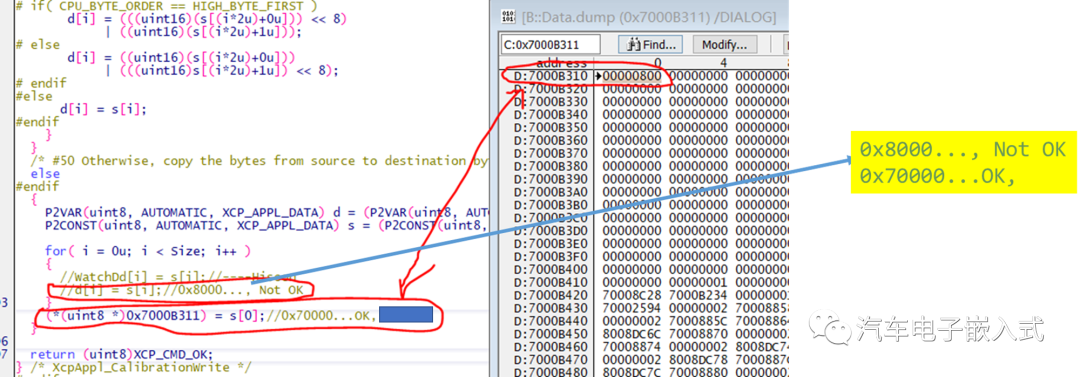
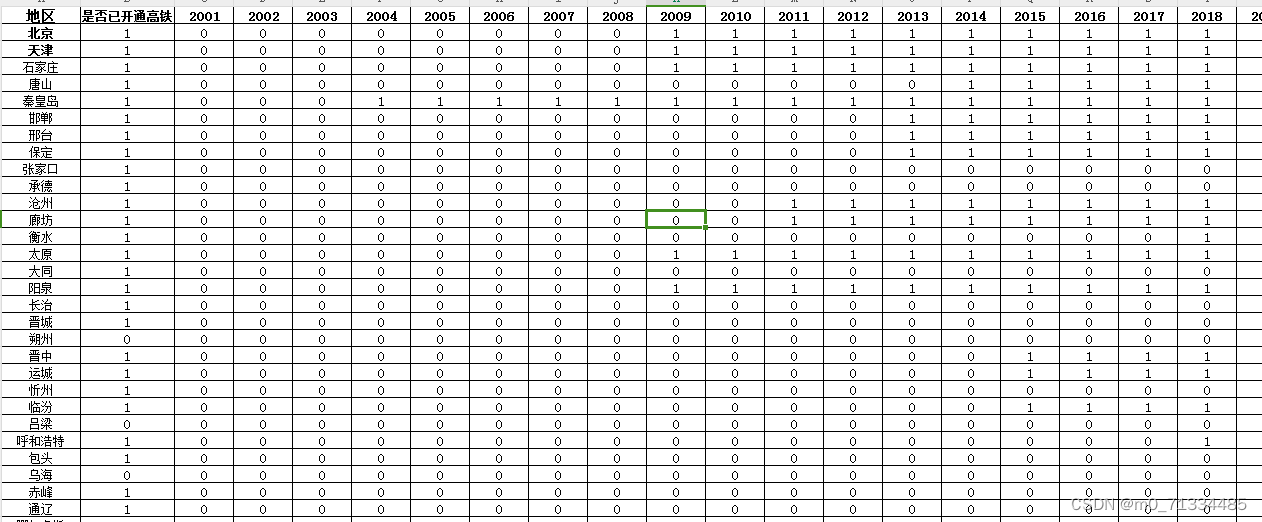
本文翻译自Cesium官方，有改动。

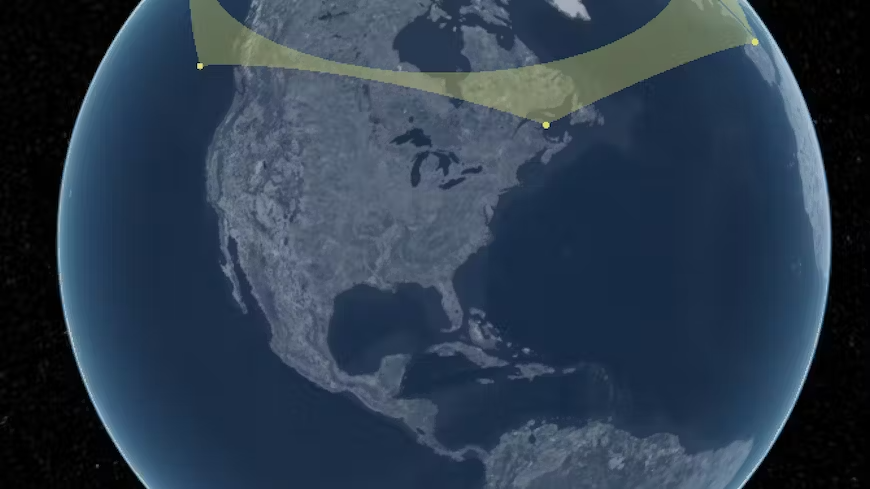
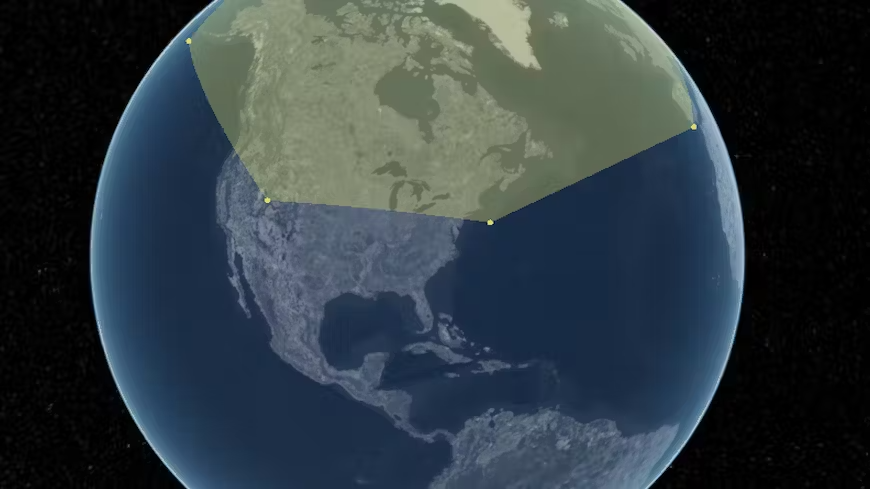
本文中提及到的“大多边形”就如下图所示。


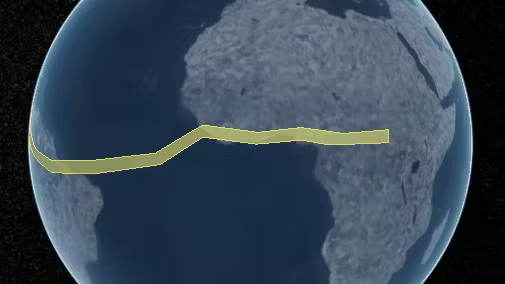
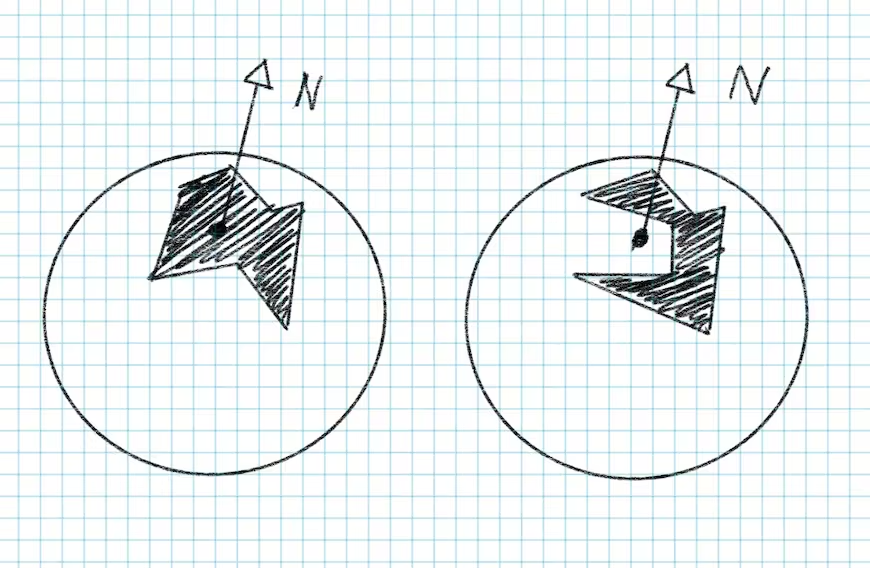
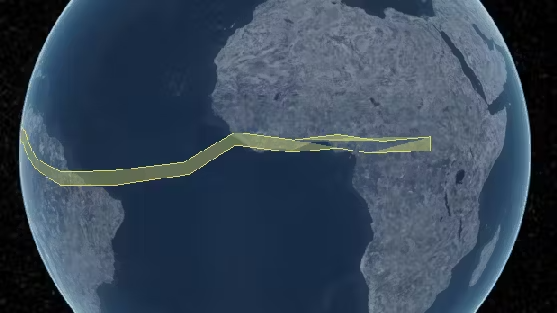
在Cesium的早期版本和一些引擎中，我们绘制这种跨度比较大的多边形，经常会看到一些奇怪的冲突问题，如下图所示。

要渲染任何几何体，我们必须将其分解为三角形以创建网格。将任意简单多边形分解为三角形的过程已在 2D 中得到了很好的实现。在CesiumJS中是使用了一个名为earcut的库，它的速度足够快，可以在浏览器中进行实时三角剖分。

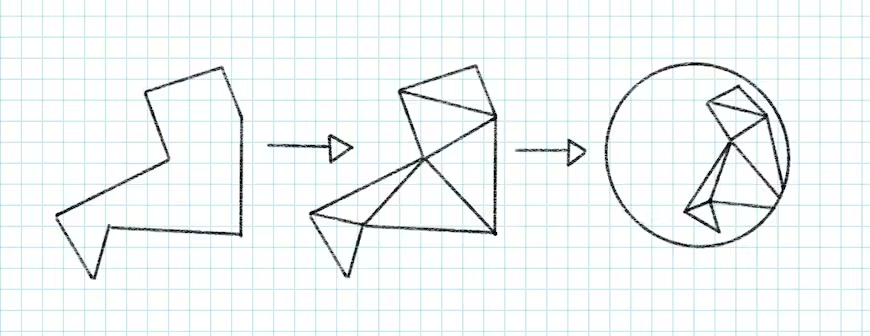
我们必须首先将多边形位置投影到二维。以前的版本中，我们总是将多边形顶点投影到与椭球体相切的平面上。这对于没有在全球范围内跨越很大范围的多边形非常有效，因为投影在接近切点时几乎不会产生失真。

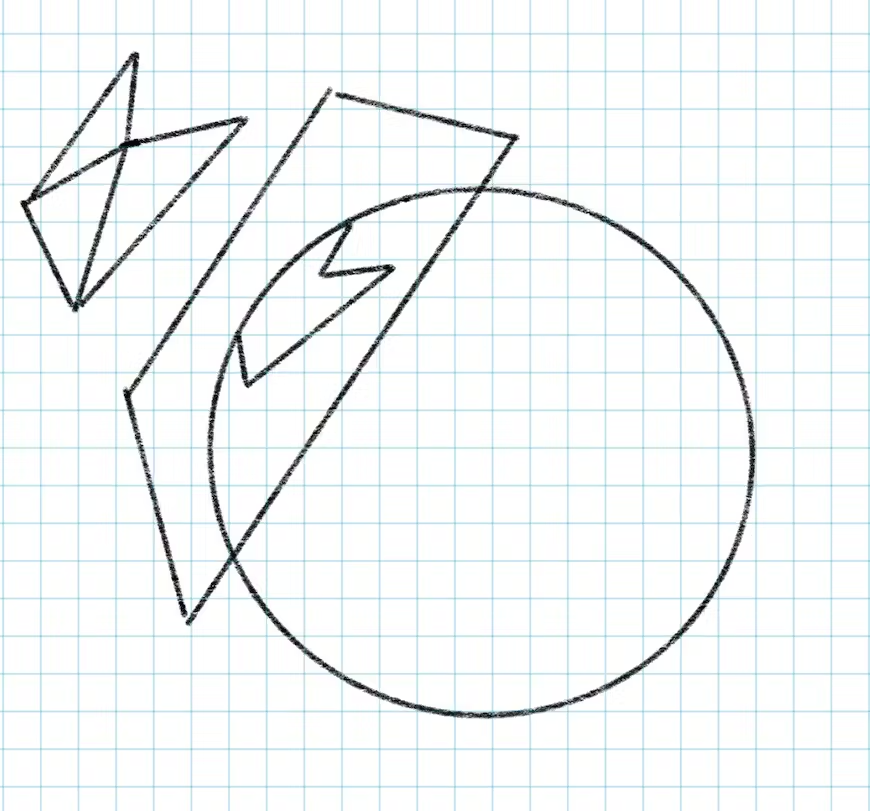
但不可能将椭球体或球体上的所有点投影到单个平面。距离切点越远，失真就越严重。对于超过 180 度的范围，到切平面的投影总是会产生不正确的结果。

一种简单的解决方案是使用多个切平面而不是仅一个。为了确保无缝网格，必须沿着每个投影区域的边缘分割多边形。

从性能的角度来看，在创建几何图形时，分割多边形可能是一项昂贵的操作，因为该算法对每个多边形和每个分割平面进行操作。但是，一旦进行三角剖分，任何分割的多边形都会稍后在管道中重新组合，作为几何批处理步骤的一部分，以确保与以前相同的渲染性能。

根据多边形的范围，只有当我们知道它足够大时，我们才可以通过执行分割操作来节省时间。但每次我们投影到不同的空间时，我们需要运行分割算法的次数越多，运行时性能的损失就越大。

即使假设范围不大于 90 度，我们也需要将多边形最多分割三次：分别在 x 轴、y 轴和 z 轴上。

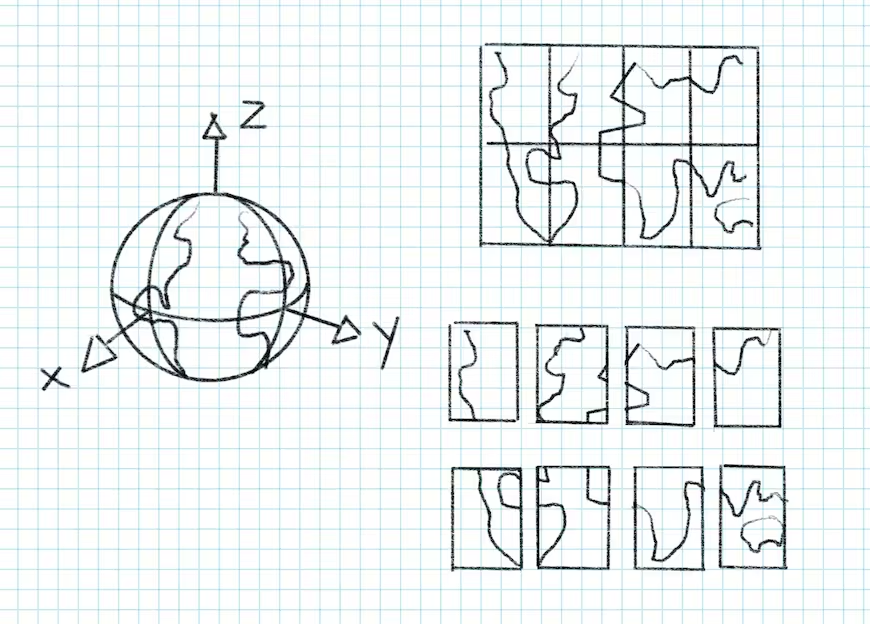
也许笛卡尔坐标系限制了我们。不同的投影怎么样？例如，立方体贴图是将 3D 球体投影到 2D 空间以渲染天空盒或环境贴图的众所周知的方法。

这里的问题是并非所有投影都是等角的；它们不能正确保留形状或点之间的相对角度。尽管它们通常会扭曲面积（这就是为什么这种类型的投影在极地区域之外的映射中不常见的原因），但保留形状对于我们在多边形上执行的几何操作至关重要。我们不仅依靠形状来保证三角剖分的准确性，而且还依赖于任何裁剪操作、确定缠绕顺序或测试极点是否位于多边形内部或外部。

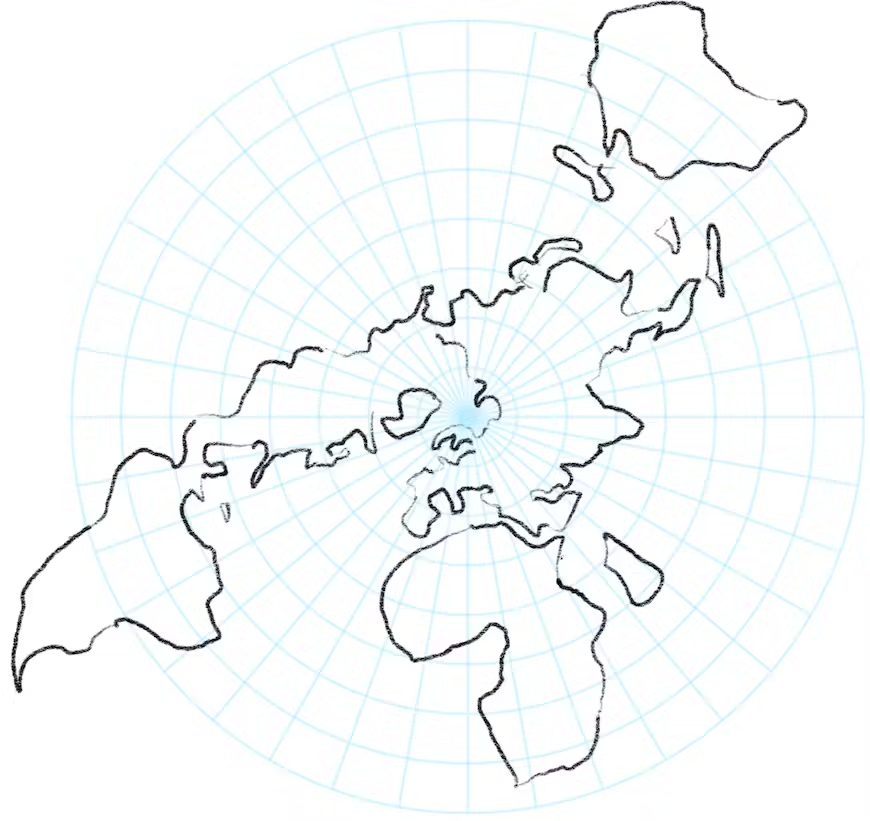
尤其是一个投影，需要分割多边形的位置很少。立体或极地 3D 笛卡尔点可以从南极投影到与北极相切的平面，反之亦然。

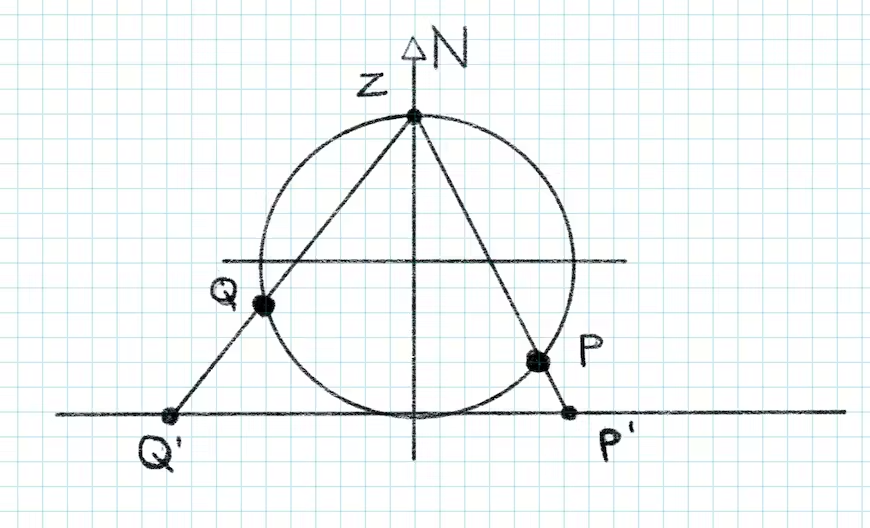
问题在于，由于小角度三角函数的精度问题，这些投影仅对略大于一个半球的区域有效。为了解决这个问题，我们在赤道处分割多边形，确保为每条边处理正确的弧类型。我们只需要在 z = 0 的平面上执行一次分割操作。在立体坐标中创建三角剖分可确保保留每个多边形位置之间的角度，即使多边形环绕椭圆体也是如此。

使用立体坐标还允许我们执行许多在球体上使用“简单”矢量数学会很棘手的操作。例如，我们现在可以根据多边形相对于原点的角度总和来确定极点是位于多边形内部还是外部，并且我们可以为多边形生成正确的制图边界。