eclipse官网https://www.eclipse.org/downloads/

软件介绍：

        Eclipse 是一个开放源代码的、基于 Java 的可扩展开发平台。Eclipse 是 Java 的集成开发环境（IDE），当然 Eclipse 也可以作为其他开发语言的集成开发环境，如C，C++，PHP，和 Ruby 等。Eclipse 附带了一个标准的插件集，包括Java开发工具（Java Development Kit，JDK）。

 一、安装eclipse之前需要配置Java环境（详见下面链接进行配置）

Windows系统Java8安装即环境配置（附安装包链接）https://blog.csdn.net/W_Fe5/article/details/131198117?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169796538416800188534615%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=169796538416800188534615&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-21-131198117-null-null.nonecase&utm_term=Java&spm=1018.2226.3001.4450

二、进入官网下载安装包

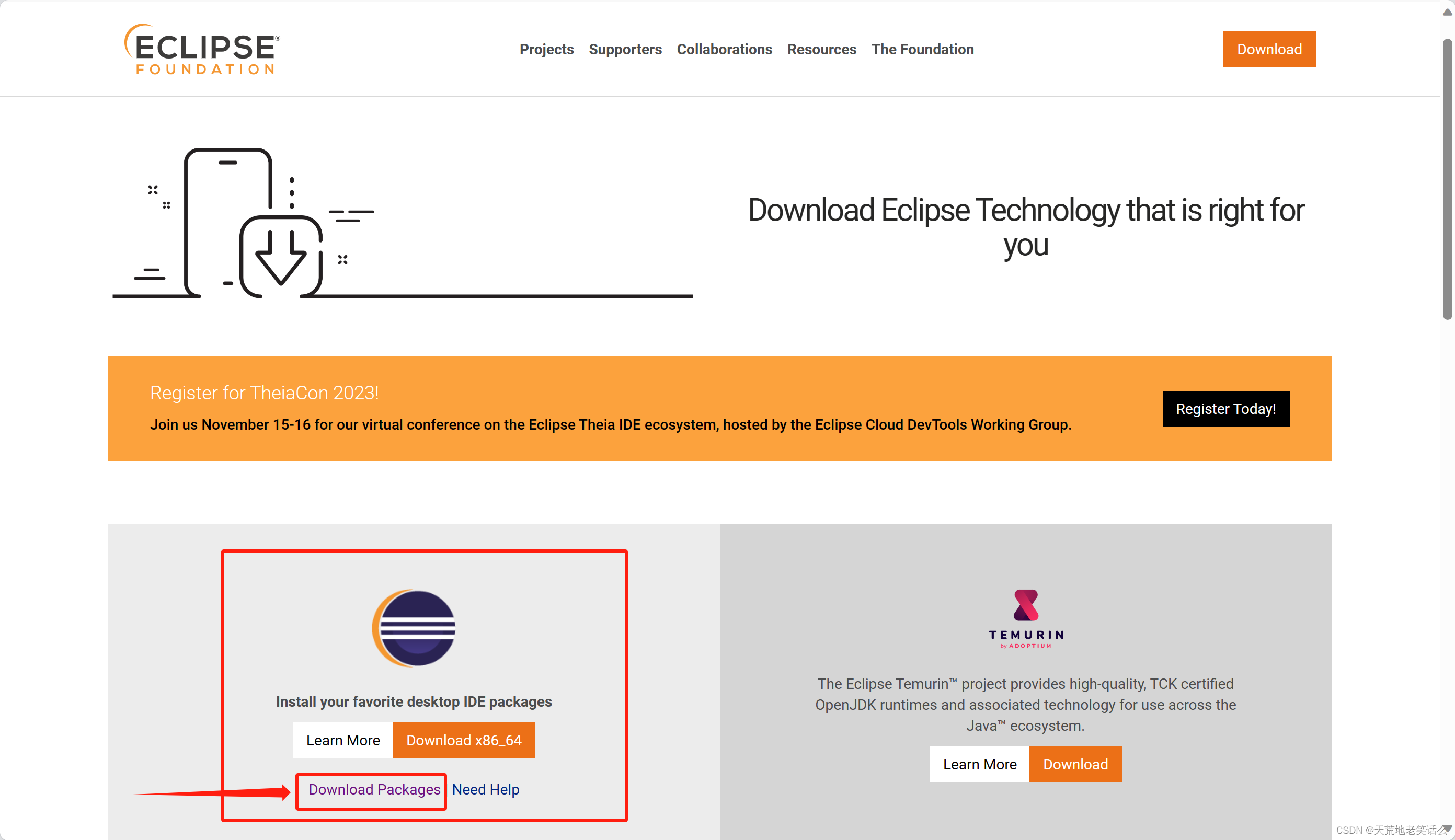
三、根据图中所示，选择window系统

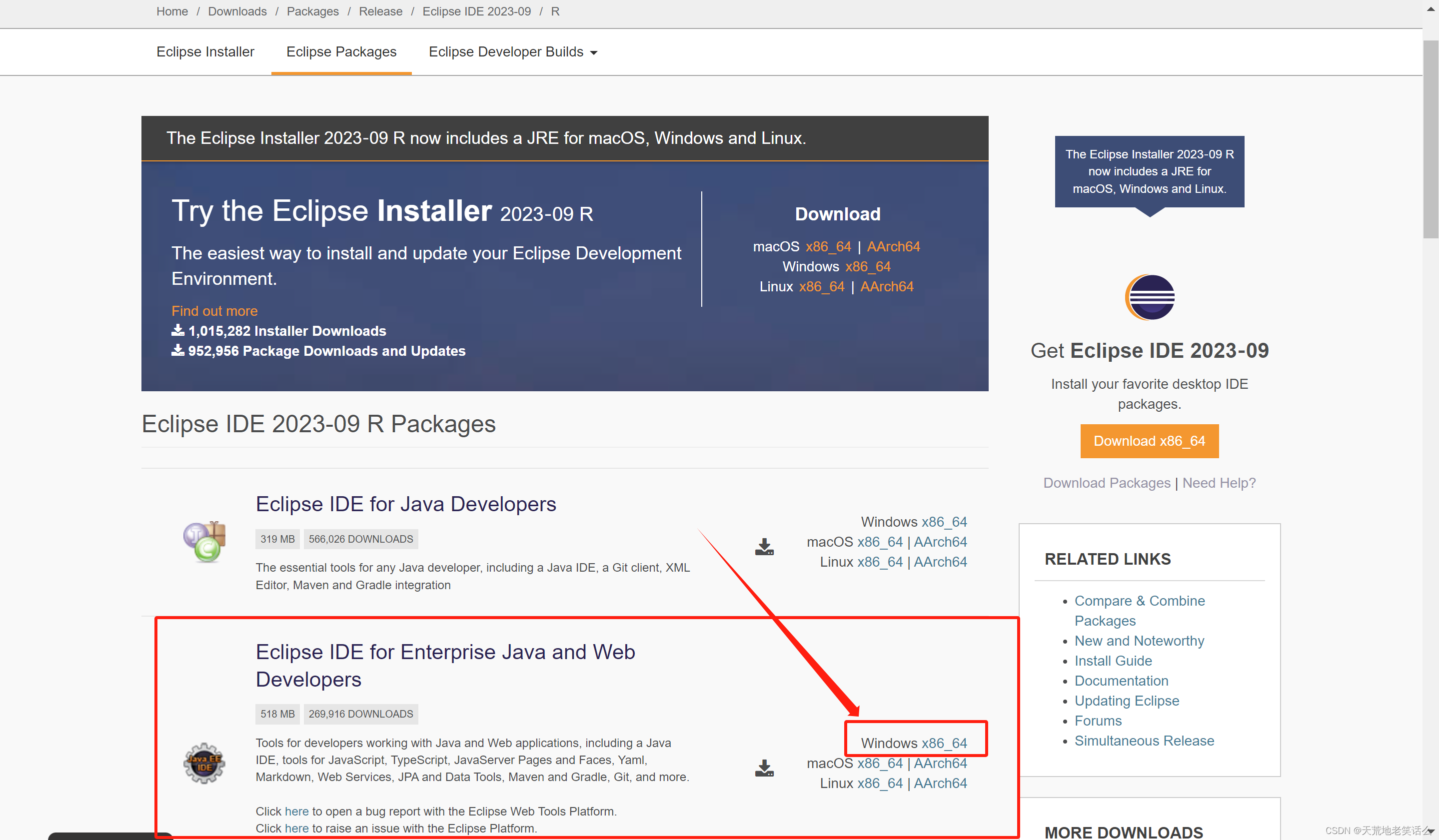
四、选择镜像，建议使用国内的，下载速度会快些（个人感觉）。

五、等待压缩包下载完成，并且解压 

六、打开解压完成的文件夹 

七、创建桌面快捷方式，方便使用 

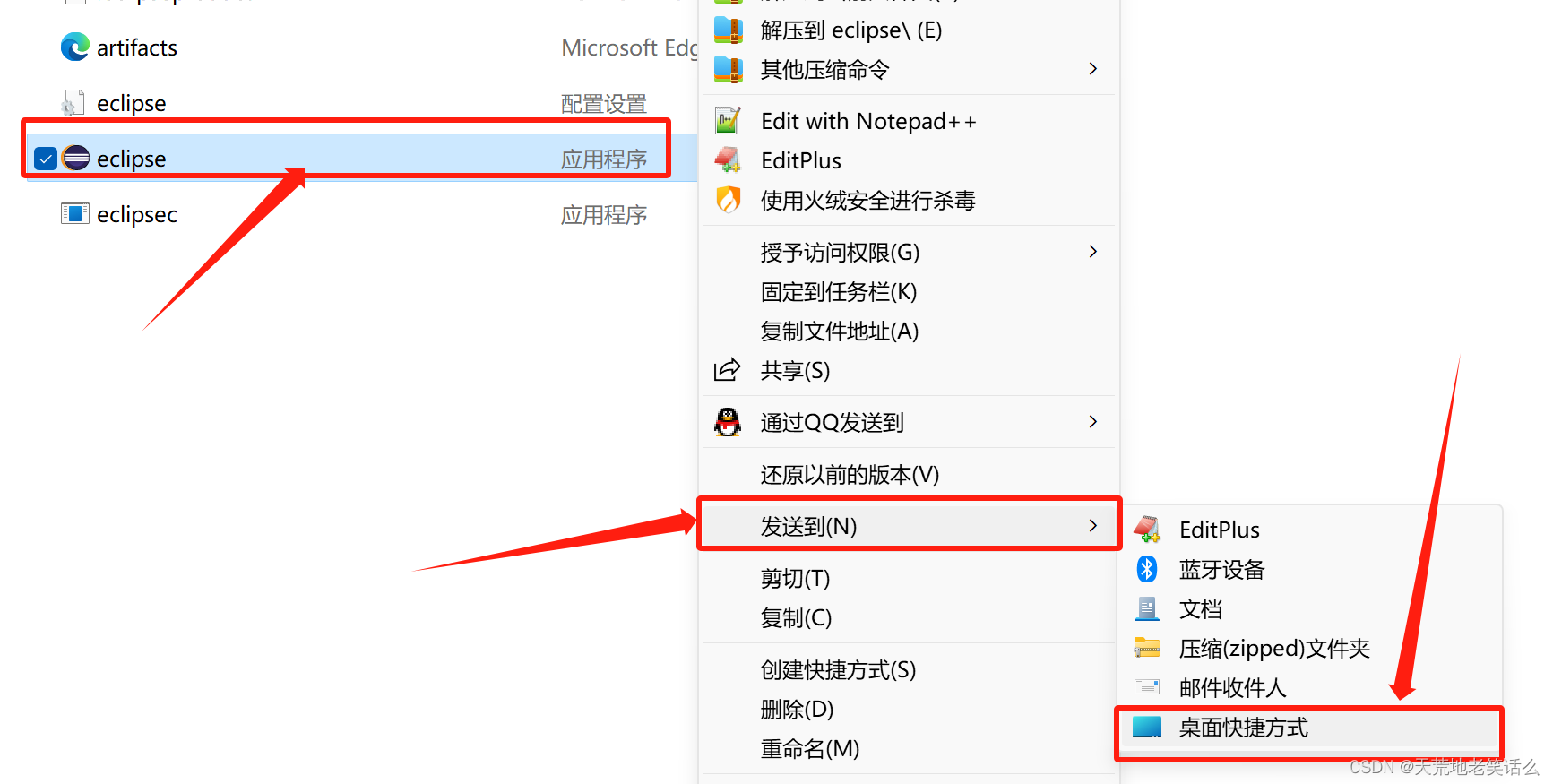
八、双击图标，打开软件 

九、 自定义路径

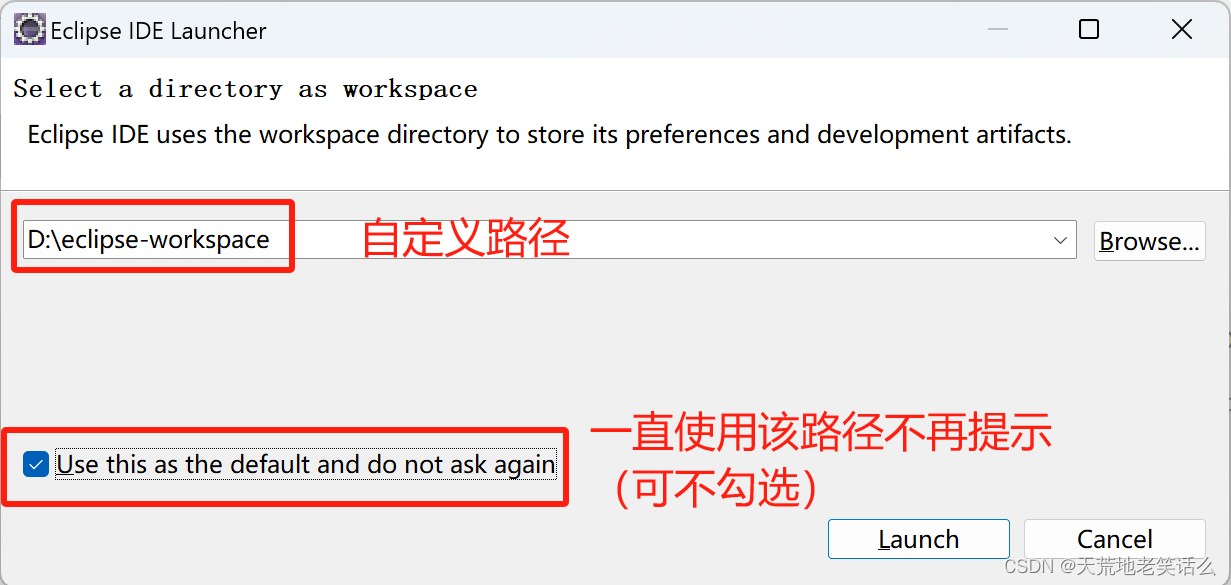
十、而后点击Launch ，等待加载完即可

十一、 安装结束，可以使用了