2023-10-21每日一题

一、题目编号

2316. 统计无向图中无法互相到达点对数

二、题目链接

点击跳转到题目位置

三、题目描述

给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [a_i, b_i] 表示节点 a_i 和 b_i 之间有一条 无向 边。

请你返回 无法互相到达 的不同 点对数目 。

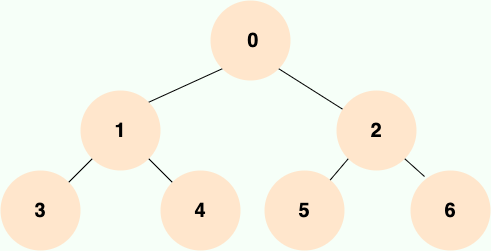
示例 1：

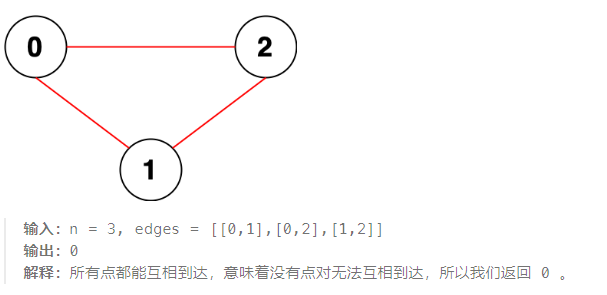
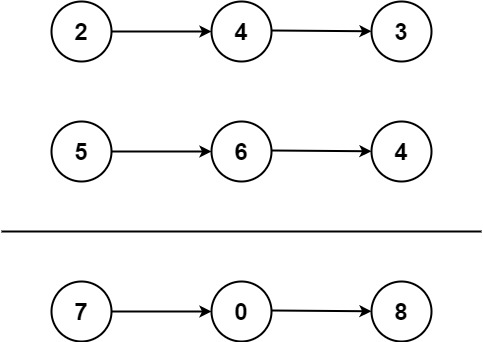
示例 2：

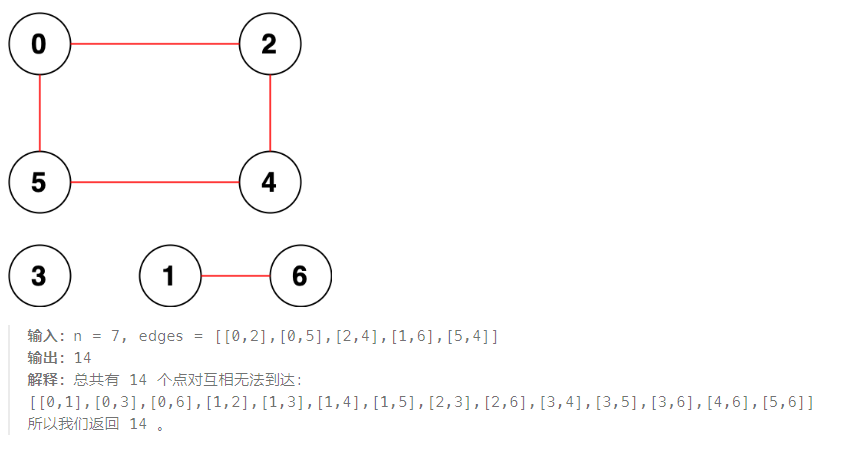
提示：

• 1 <= n <= 10⁵
• 0 <= edges.length <= 2 * 10⁵
• edges[i].length == 2
• 0 <= a_i, b_i < n
• a_i != b_i
• 不会有重复边。

四、解题代码

class Solution {
public:
    long long countPairs(int n, vector<vector<int>>& edges) {
        long long sum = 0;
        vector<int> Edge[100010];
        for(int i = 0 ;i < n; ++i){
            Edge[i].clear();
        }
        for(int i = 0; i < edges.size(); ++i){
            int x = edges[i][0];
            int y = edges[i][1];
            Edge[x].push_back(y);
            Edge[y].push_back(x);
        }
        int hash[100010];
        memset(hash,0,sizeof(hash));
        vector<int> res;
        for(int i = 0 ;i < n; ++i){
            if(hash[i] == 0){
                int cnt = 1;
                hash[i] = 1;
                queue<int> q;
                q.push(i);
                while(!q.empty()){
                    int x = q.front();
                    q.pop();
                    for(int j = 0; j < Edge[x].size(); j++){
                        int t = Edge[x][j];
                        if(hash[t] == 0){
                            hash[t] = 1;
                            cnt++;
                            q.push(t);
                        }
                    }
                }
                res.push_back(cnt);
            }
        }
        for(int i = 0; i < res.size(); ++i){
            sum += (long long)res[i]*(res[i]-1)/2;
        }
    return (long long)n*(n-1)/2-sum;
    }
};

五、解题思路

(1) 广度优先搜索。