现在跟的是 b站黑马 的视频课,还是这个好哇
2023新版数据结构与算法Java视频教程(上篇)
2023新版数据结构与算法Java视频教程(下篇)
之前跟的是 青岛大学 张公敬教授 的《算法设计与分析》(做了笔记就发出来吧)
mooc:算法设计与分析_青岛大学_中国大学Mooc(慕课)
b站:算法设计与分析MOOC-青岛大学-张公敬教授
用的是 王晓东的《计算机算法设计与分析》 ,虽然书名不同,但是里面的内容和算法是差不多的。
个人觉得应付专业课学前四章就够了,把一些经典的入门算法题刷一刷记下来就够用了。
第 1 章 算法入门
1.1 算法概论
1.2 求两个正整数的最大公约数的 3 种算法
计算两个正整数 m , n 的最大公约数
1.2.1 欧几里德算法 gcd(m,n)
其中 m > n ,其递归定义为:
gcd(m,n) = m , n=0
gcd( n , m mod n ) , n>0
gcd(60,24)
gcd(60,24) =
∵ 60 / 24 = 2 余 12 ∴ m = 24 n = 12
gcd(24,12) =
∵ 24 / 12 = 2 余 0 ∴ m = 12 n = 0
gcd(12,0) = 12
自然语言描述
第一步:如果 n = 0,返回 m 的值作为结果,同时过程结束;否则,进入 第二步。
第二步:用 n 去除 m ,将余数赋给 r 。
第三步:将 n 的值赋给 m ,将 r 的值赋给 n ,返回 第一步。
伪代码描述
算法 Euclid(m,n)
//使用欧几里德算法计算 gcd(m,n)
//输入:两个不全为零的非负整数 m,n
//输出:m,n 的最大公约数
while n <> o dor
r ← m mod n
m ← n
n ← r
return m
Java语言描述
算法 Euclid(m,n)
//使用欧几里德算法计算 gcd(m,n)
//输入:两个不全为零的非负整数 m,n
//输出:m,n 的最大公约数
//使用欧几里德算法计算 gcd(m,n)
//输入:两个不全为零的非负整数 m,n
//输出:m,n 的最大公约数
public static int gcd(int m,int n) {
// 第一种写法
int r;
while(n != 0) {
r = m % n;
m = n;
n = r;
}
return m;
// 第二种写法
// if(n == 0) return m;
// return gcd(n, m%n);
}
其他描述方式
- 流程图
- N-S图
- 等等
- 各种描述方法都有一定的优缺点
1.2.2 连续整数检测算法
算法思想
基于最大公约数的定义:同时整除两个整数的最大整数
显然,不会大于两数较小者。
故令: t = min{m , n}
用 t 除 m ,n ,若除尽, t 即最大公约数;
否则令:= t - 1 ,继续尝试。
gcd(60,24)
∵ t = 24 无法同时除尽60,24
∴ t = 23
∵ t = 23 无法同时除尽60,24
∴ t = 22
······
∵ t = 12 无法同时除尽60,24
∴ 返回 t 的值
自然语言描述
第一步:将 min{m,n} 的值赋给 t 。
第二步:m 除以 t ,如果余数为 0 ,进入第三步;否则,进入第四步。
第三步:n 除以 t ,如果余数为 0 ,返回 t 值作为结果;否则,进入第四步。
第四步:将 t 值减 1 。返回第二步。
1.2.3 因式分解
思路
把 2···n 之间的所有素数找出来,逐个逐个测试出 m , n 中包含的公共素因子,将公共的素因子相乘就得到最大公约数。
∵ 60 = 2 x 2 x 3 x 5
24 = 2 x 2 x 2 x 3
∴ gcd(60,24) = 2 x 2 x 3 = 12
新问题:如何快速找出 2···n 之间的所有素数?
埃拉托色尼筛算法
算法思想
- 首先初始化一个 2~n 的连续序列,作候选质数。
- 第一个循环消去 2 的倍数,
- 然后,指向序列的下一个数字 3 ,消去其倍数,
- 接下来指向 5 ,消去其倍数,
- 按此方法不断做下去,直到序列中没有可消元素
小结
本节主要内容
- 算法的定义与性质
- 解决问题的流程
- 以求最大公约数为例了解算法的描述方法
- 以求最大公约数为例证明算法的正确性
1.3 算法时间复杂度计算方法

1.4 算法时间复杂度的表示方法
递归算法
非递归算法
1.5 主定理方法解递归方程
1.5.1 递推方法求递归算法的时间复杂性
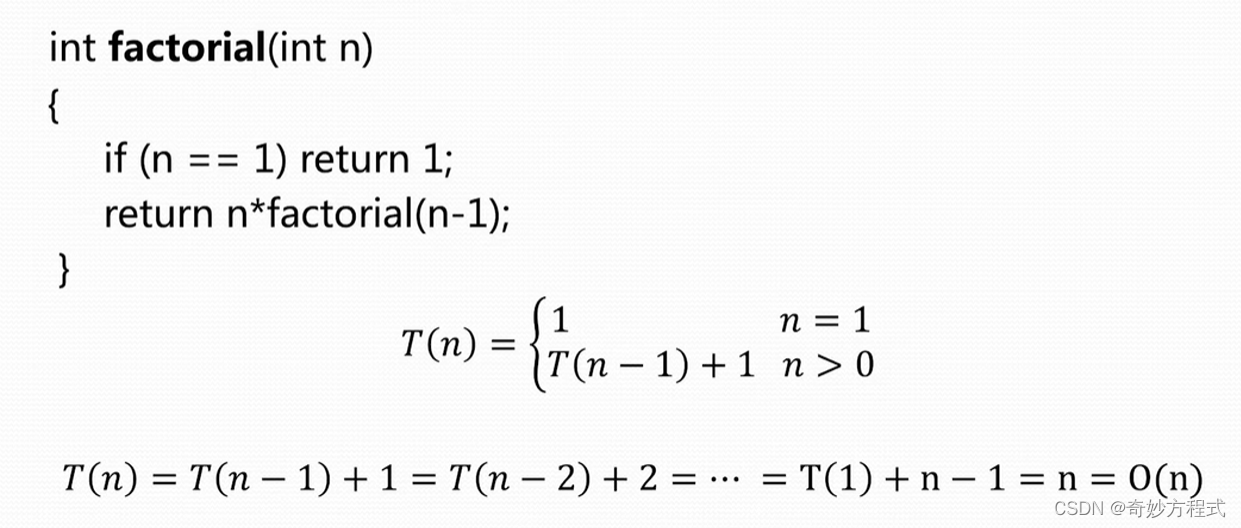
1.5.2 Master 定理方法求递归算法时间复杂性