Description
求N!的因子数%10^9+7
1≤N≤1000000
Format
Input
一行给出数字N
N<=1000000
Output
如题
Samples
输入数据 1
3
Copy
输出数据 1
4
Copy
输入数据 2
100
Copy
输出数据 2
583951250一,朴素解法
思路:
直接算出n!是多少,再求它的因子数即可。
(由于这种做法太简单,我这里就不板书代码了qwq)
分析:
就算开了long long,n到20左右算n!就会爆空间,何况这里n最多是1000000。况且就算没爆空间算出1000000!后求他的因子数也会超时。(毕竟这数太大了)
二,巧用因数个数定理
思路:
一个数的约数是由这个数的几个质因子相乘得到的。
例如:12 的质因子有 2,3。12的约数有:1,2,3,4,6,12。
...约数1 是由 0 个 2, 0 个3相乘得到的。
...约数2 是由 1 个 2, 0 个3相乘得到的。
...约数3 是由 0 个 2, 1 个3相乘得到的。
...约数4 是由 2 个 2, 0 个3相乘得到的。
...约数6 是由 1 个 2, 1 个3相乘得到的。
...约数12 是由 2 个 2, 1 个3相乘得到的。
12 可以分解为:2^2*3^1。所以2可以取 0 ~ 2个,3种取法。3可以取 0~1 个,2种取法。12的质因子一共:2 * 3 = 6个。
也就是:把一个数N 写成:N = (p1^x1^)(p^x2)(p3^x3)…(pk^xk),其中pi为质数。则N的约数个数为:(x1+1)(x2+1)(x3+1)…(xk+1)。
那么这道题就只需要枚举1~n,再把每个数按上述公式操作一遍即可。
注意:如果存储各个质因子的个数用数组来存储的话会爆空间,所以此处因用map。
代码:
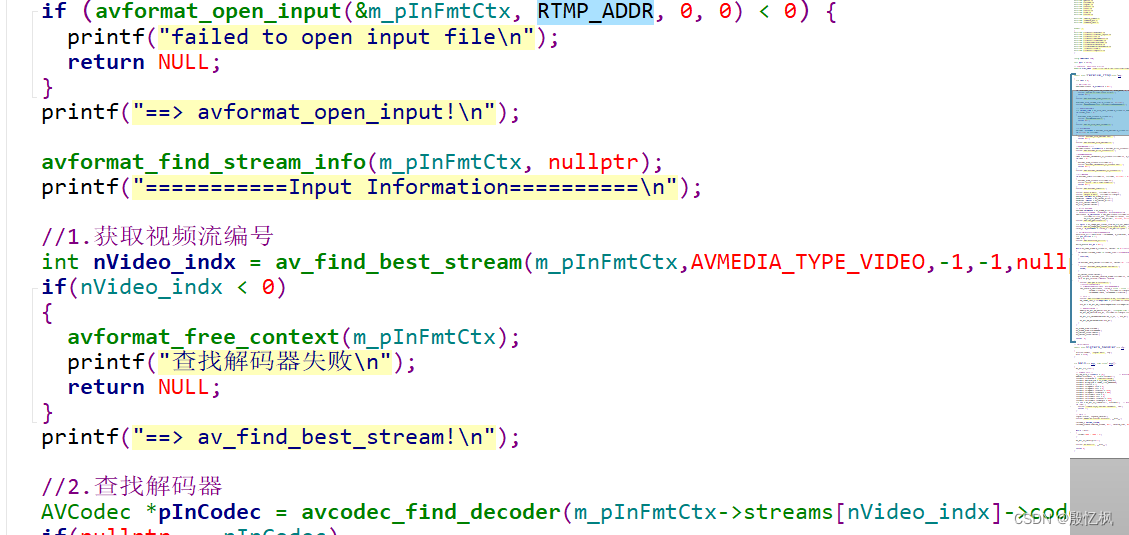
#include <bits/stdc++.h>
using namespace std;
long long ans = 1,n,x = 1,mod = 1000000007,s = 1;
unordered_map<long long,long long> mp;
int main()
{
scanf("%lld",&n);
while(n--)
{
x = s;
for(long long i = 2; i <= x / i; i++)
{
while(x % i == 0)
{
x /= i;
mp[i]++;
}
if(x == 1) break;
}
if(x > 1) mp[x]++;
s++;
}
for(auto i : mp) ans *= (i.second + 1),ans %= mod;
printf("%lld",ans);
return 0;
}分析:
上述程序的时间复杂度为O(n* log(n))左右,如果运行以上程序会发现,当n = 1000000时还是会超时。那么该怎么办呢?
三,最终解法
思路:
我们应该换个角度想,
对于1到N之间的数字,一个个去分解质因子,是一种比较原始的想法
为什么不换个角度去想
例如N=100
则对于质因子2,能不能找出1到N之间的数字,能批量产生多少个2出来呢?
则对于质因子3,能不能找出1到N之间的数字,能批量产生多少个3出来呢?
则对于质因子5,能不能找出1到N之间的数字,能批量产生多少个5出来呢?
……
那么新问题又来了:我们该怎么快速找出1~n中包含多少个目前枚举出的质因子呢?
此时,我们应该想到曾经做过的一道题:求N!后面有多少个连续的零_玲珑看秋月的博客-CSDN博客
那道题中我们是求 1~n的质因子中包含多少个5,那么我们不就可以枚举1~n中的质数,然后用那道题的方法求出1~n中包含多少个目前枚举出的质因子,再利用因数个数定理求出答案了吗?
代码:
#include <bits/stdc++.h>
using namespace std;
long long ans = 1,n,x = 1,mod = 1000000007,s,pris,pri[10000001];
bool isp[10000001];
unordered_map<long long,long long> mp;
int main()
{
scanf("%lld",&n);
memset(isp,1,sizeof(isp));
isp[1] = 0;
for(long long i = 2;i <= n;i++)
{
if(isp[i] == 1) pri[++pris] = i;
for(long long j = 1;i * pri[j] <= n;j++)
{
isp[i * pri[j]] = 0;
if(i % pri[j] == 0) break;
}
}
for(long long j = 1;j <= pris;j++)
{
long long i = pri[j];
s = 0;
long long t = i;
while(t <= n)
{
s += n / t;
t *= i;
}
ans *= (s + 1);
ans %= mod;
}
printf("%lld",ans);
return 0;
}