文章目录
- 一、岁数
- 1、题目
- 2、思路讲解
- 3、代码实现
- 4、结果
- 二、打碎的鸡蛋
- 1、题目
- 2、思路讲解
- 3、代码实现
- 4、结果
- 三、分糖
- 1、题目
- 2、思路讲解
- 3、代码实现
- 4、结果
- 四、兔子产子
- 1、题目
- 2、思路讲解
- 3、代码实现
- 4、结果
- 五、矩阵问题
- 1、题目
- 2、思路讲解
- 3、代码实现
- 4、结果
- 六、谁是窃贼问题
- 1、题目
- 2、思路讲解
- 3、代码实现
- 4、结果
- 七、娶公主
- 1、题目
- 2、思路讲解
- 3、代码实现
- 4、结果
一、岁数
1、题目
一位学生说“我的岁数的三次方是个四位数,四次方是个六位数。要组成我岁数的三次方和四次方,需要用遍0~9十个数字。”请问他多少岁?
2、思路讲解
从10开始遍历,先算出i的三次方和四次方,然后遍历求三次方,四次方的每一位,这里使用了^ 异或运算符,如果每位有相同的数字,b就会为0,就不符合条件,就终止循环。
3、代码实现
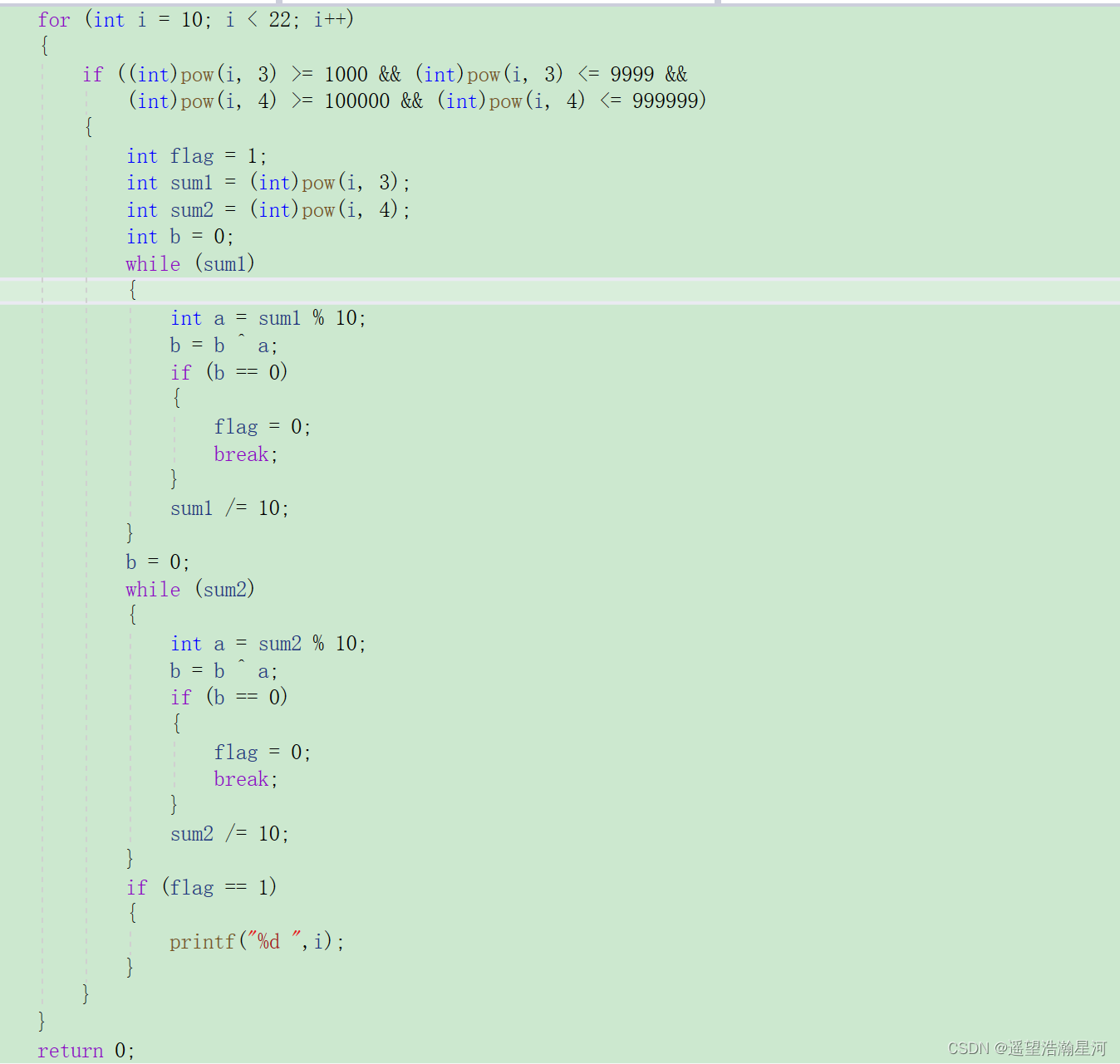
4、结果
二、打碎的鸡蛋
1、题目
某女士手里拎了一篮鸡蛋,从她身边奔跑而过一匹惊马,吓了她一跳,结果把篮里的鸡蛋,她说两个一数,三个一数,四个一数,五个一数时,余数分别为1,2,3和4。问篮里原有多少个鸡蛋?
2、思路讲解
解决这类问题的要点就是找到一个最大的数作为步长,以减少其循环次数,该例题的最大数为5,故应以5为步长,这里因为我们不知道鸡蛋的个位,所以不设置循环终止条件,终止由break来决定。
3、代码实现
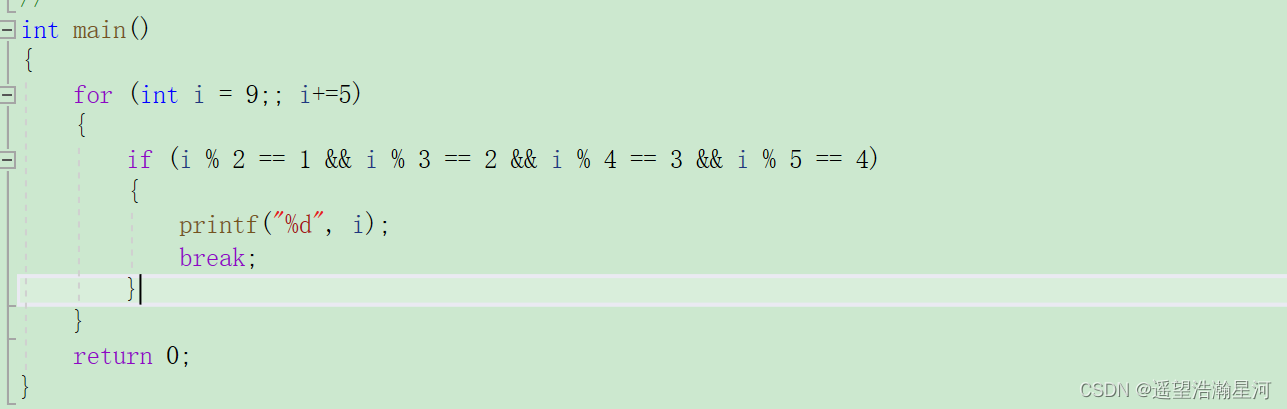
4、结果
三、分糖
1、题目
新年晚会老师给大家分糖,手端着一盘糖,让第一个同学先拿1块糖,再把盘中的糖分1/7给他;然后让第二个同学拿2块糖,再把盘中的糖的1/7给他;第三个同学拿3块糖后,仍把盘中的糖的1/7给他。照这个办法分下去,最后一个同学自己拿完糖后,糖恰好分完,而且每个人分到的糖块数相同。问共有几人?每人分几块糖?
2、思路讲解
最后一个同学自己拿完糖后,糖恰好分完”以及前面的条件可知,最后一个同学所拿的糖的数量刚好等于人数。再根据其他条件可知,第i个同学所拿的糖的数量为所剩下糖的1/6加上i,并且每个同学所拿的糖的数量必为整数,
3、代码实现

4、结果
四、兔子产子
1、题目
有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子,假如兔子都不死,问一年内兔子总数是多少?第18个月的兔子数为多少?
2、思路讲解
第1个月与第2个月都只有一对兔子,第3个月它们产下一对小兔子,共有2对兔子;第4个月老兔子又产下一对小兔子,共有3对兔子;第5个月老兔子又产下一对小兔子,两个月前的小兔子也产下一对小兔子,共有5对兔子;依次类推,找出每个月兔子对数的规律。
每个月的兔子对数,1,1,2,3,5,8…… 可以看出 形如斐波那契数。
3、代码实现
递归解法

非递归解法

4、结果
五、矩阵问题
1、题目
输入一个数字n,得到一个n*n的矩阵,按如下规则给矩阵填入数字:
(1)如果n为奇数,将矩阵的上三角按顺时针方向填入递增的数据(如图1所示)。
(2)如果n为偶数,将矩阵的下三角按逆时针方向填入递增的数据(如图2所示)。
(建议输入的值在3-10之间)
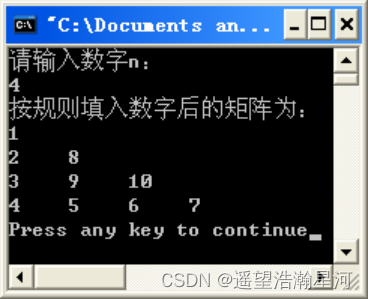
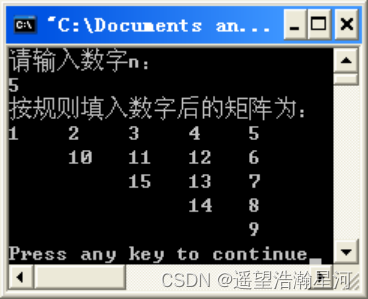
2、思路讲解
定义存放矩阵数据的数组,首先确定第一圈(最外圈)的数据,并根据输入的数字n的奇偶性,将从1开始的递增的数据存放在相应的数组元素中,然后再确定第二圈的数组元素值,依次类推,直到填满题目要求的数组元素值(n为奇数填满上三角,n为偶数填满下三角)。
3、代码实现
int main()
{
int n;
scanf("%d", &n);
int a[10][10] = { 0 };
if (n % 2 == 0)
{
int p = 1;
for (int i = 0; i < n; i++)
{
for (int j = 0; j <= i; j++)
{
if (j == 0)
{
a[i][j] = i + 1;
}
else if (i == n - 1)
{
a[i][j] = i + j + 1;
}
else
{
a[i][j] = (2 * n - 1) + p;
p++;
}
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j <= i; j++)
{
printf("%-3d ", a[i][j]);
}
printf("\n");
}
}
else
{
int p = 1;
for (int i = 0; i < n; i++)
{
for (int j = i; j < n; j++)
{
if (i == 0)
{
a[i][j] = j + 1;
}
else if (j == n - 1)
{
a[i][j] = a[0][n - 1] + i;
}
else
{
a[i][j] = (2 * n - 1) + p;
p++;
}
}
}
for (int i = 0; i < n; i++)
{
for (int k = 1; k <= i; k++)
{
printf(" ");
}
for (int j = i; j < n; j++)
{
printf("%-3d ", a[i][j]);
}
printf("\n");
}
}
return 0;
}
4、结果
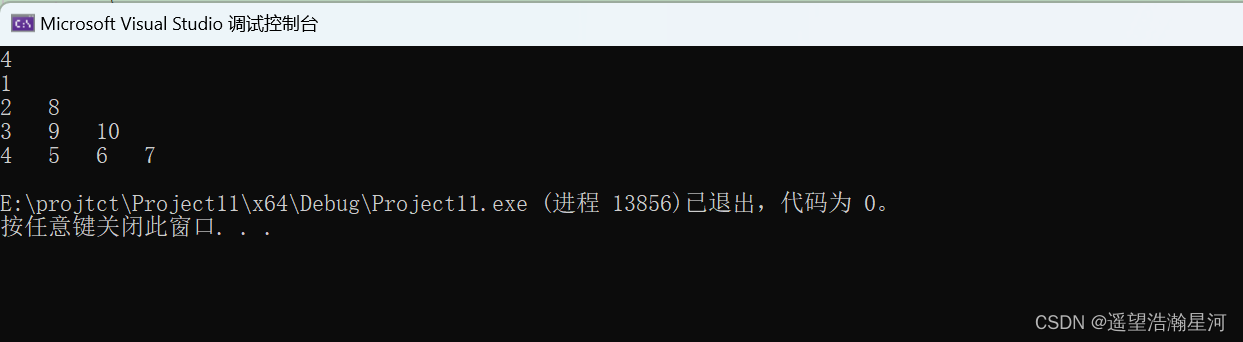
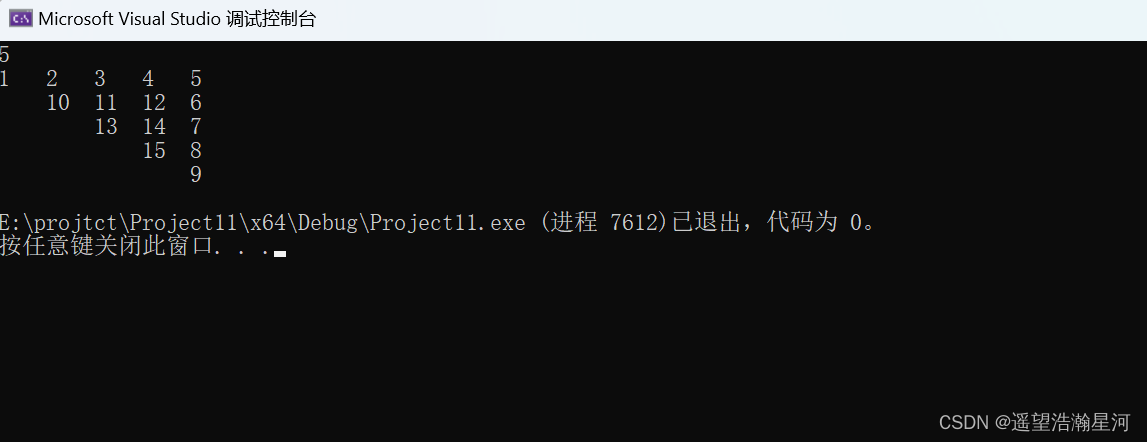
六、谁是窃贼问题
1、题目
警察审问四名窃贼嫌疑犯。已知,这四人当中仅有一名是窃贼,还知道这四个人中每人要么是诚实的,要么总是说谎。他们给警察的回答是:
甲说:“ 我没有偷。”
乙说:“ 甲没有偷,是丙偷的。”
丙说:“ 我没有偷,是丁偷的。”
丁说:” 丙没有偷,是乙偷的。”
请根据这四个人的回答判断谁是窃贼。
2、思路讲解
假设用A、B、C、D分别代表这四个人,变量的值为1代表该人是窃贼,则根据四个人的说法可列出4个条件。例如,根据乙说的话,可以列出条件:A+C=1。
3、代码实现
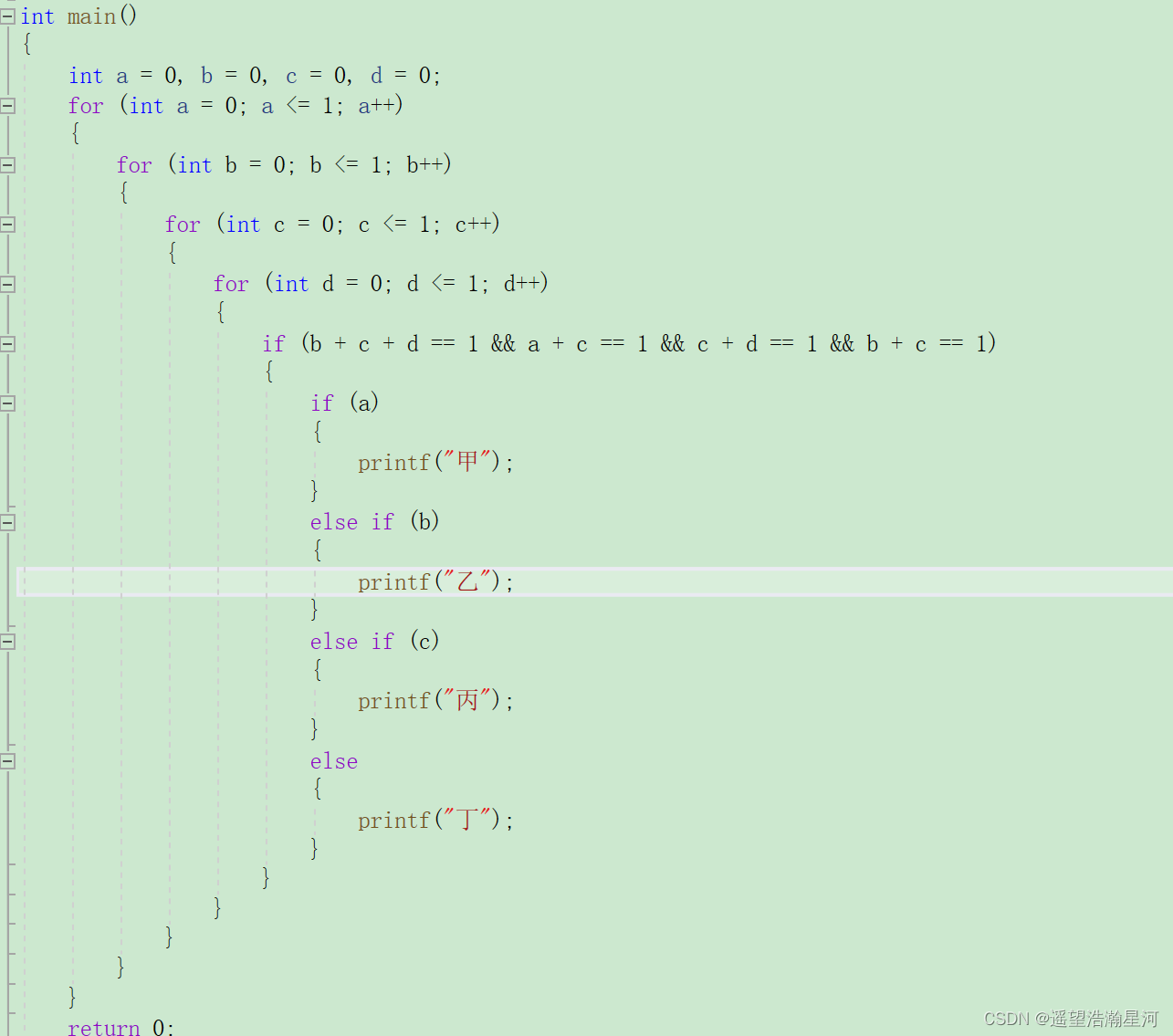
4、结果
七、娶公主
1、题目
若干求婚者排成一行,一二报数,报单数的退场。余下的人靠拢后再一二报数,报单数的退场,最后剩下的一位就可以娶公主为妻。若现在你站出来数一下,共有101人在你前面,你应站到哪一个位置才能娶到公主呢?
2、思路讲解
首先将1到103存在到数组中,然后循环,总数除以2,并且重复将双数存在到数组中,当循环终止的时候,剩下的那个数就是最好的位置。
3、代码实现

4、结果