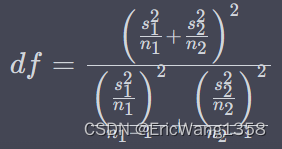本文解决的问题：双系统装完后需要删除ubuntu的分区，但是EFI系统分区无法删除。

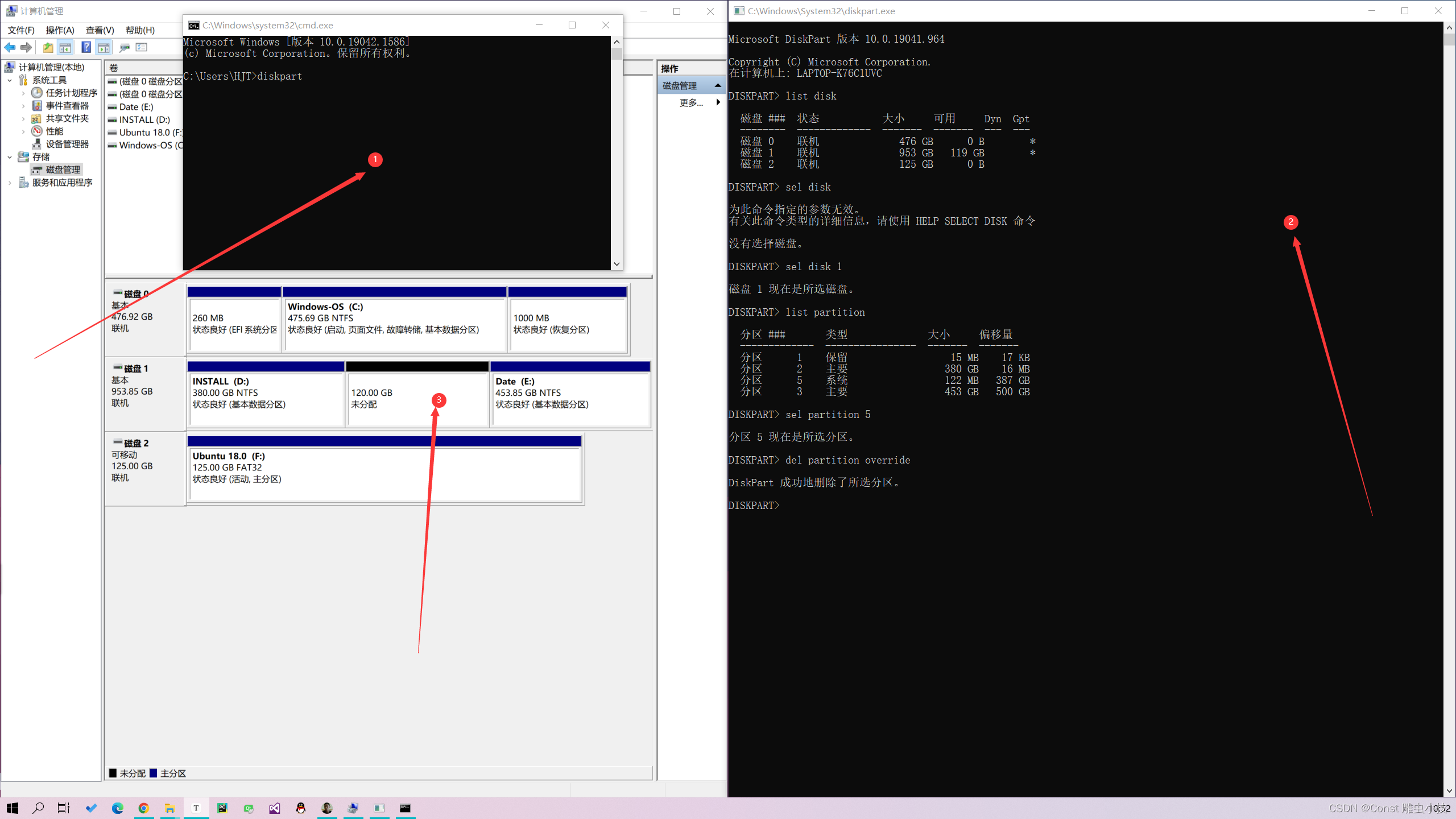
第一步：cmd中输入命令 diskpart 并回车，如图中①；

第二步：在弹出窗口②中依次输入如下命令即可删除EFI分区；

//磁盘列表
list disk

//选择分区所在的磁盘x（x为磁盘序号）
sel disk x

//列出磁盘x的分区
list partition

//选择磁盘x的分区m（m为分区名）
sel partition m

//删除所选分区
del partition override