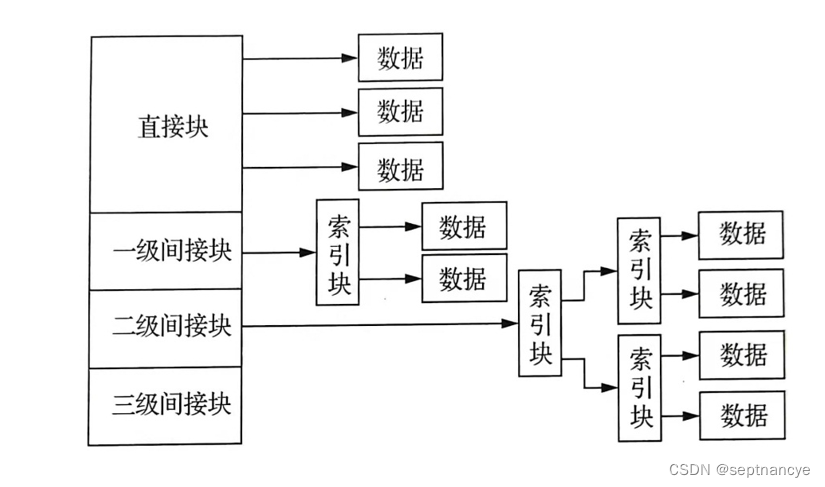
相信大家在平时的期末考试中一定少不了对某某向量组执行标准正交化类型的题目。今天我们从这个题目入手,说明这个如何执行施密特正交化,以及为什么要进行正交化。


一、例子
例子:设 a 1 = [ 1 2 − 1 ] a_1=\begin{bmatrix}1\\2\\-1\end{bmatrix} a1= 12−1 , a 2 = [ − 1 3 1 ] a_2=\begin{bmatrix}-1\\3\\1\end{bmatrix} a2= −131 , a 3 = [ 4 − 1 0 ] a_3=\begin{bmatrix}4\\-1\\0\end{bmatrix} a3= 4−10 使用施密特正交化将这组向量标准正交化。
答:标准正交向量组应该满足:
- 向量的长度为1;
- 向量之间相互正交;
选定一个基准向量
A
1
=
a
1
=
[
1
2
−
1
]
A_1=a_1=\begin{bmatrix}1\\2\\-1\end{bmatrix}
A1=a1=
12−1
对第二个向量分解为正交和与
A
1
A_1
A1 共线的两个向量,其中与
A
1
A_1
A1 共线的向量因为已经能够用
A
1
A_1
A1 进行表示,所以应该剔除只保留与
A
1
A_1
A1 正交的分量:
A
2
=
A
2
−
P
A
1
A
2
=
A
2
−
A
1
A
1
T
A
1
T
A
1
A
2
=
5
3
[
−
1
1
1
]
A_2=A_2-P_{A_1}A_2=A_2-\frac{A_1A_1^T}{A_1^TA_1}A_2=\frac{5}{3}\begin{bmatrix}-1\\1\\1\end{bmatrix}
A2=A2−PA1A2=A2−A1TA1A1A1TA2=35
−111
同理:
A
3
=
A
3
−
A
2
A
2
T
A
2
T
A
2
A
3
−
A
3
A
3
T
A
3
T
A
3
A
3
=
2
[
1
0
1
]
A_3=A_3-\frac{A_2A_2^T}{A_2^TA_2}A_3-\frac{A_3A_3^T}{A_3^TA_3}A_3=2\begin{bmatrix}1\\0\\1\end{bmatrix}
A3=A3−A2TA2A2A2TA3−A3TA3A3A3TA3=2
101
已经正交化的向量应该更新到下一个阶段的计算。
接下来对向量组的每个成员进行单位化。
单位化的长度可以随便缩小,总之保证模长度为1即可,也就是说前面的诸如 2 2 2 和 5 3 \frac{5}{3} 35 完全不用考虑其存在。
e 1 = A 1 ∣ A 1 ∣ = 1 6 [ 1 2 − 1 ] e 2 = A 2 ∣ A 2 ∣ = 1 3 [ − 1 1 1 ] e 3 = A 3 ∣ A 3 ∣ = 1 2 [ 1 0 1 ] e_1=\frac{A1}{|A1|}=\frac{1}{\sqrt 6}\begin{bmatrix}1\\2\\-1\end{bmatrix}\\ e_2=\frac{A2}{|A2|}=\frac{1}{\sqrt 3}\begin{bmatrix}-1\\1\\1\end{bmatrix}\\ e_3=\frac{A3}{|A3|}=\frac{1}{\sqrt 2}\begin{bmatrix}1\\0\\1\end{bmatrix} e1=∣A1∣A1=61 12−1 e2=∣A2∣A2=31 −111 e3=∣A3∣A3=21 101
如果你动手计算的话,你会发现得到正交化的结果并不容易。所以为什么我们要废这么大功夫去实现这样的一个分解?接下来就是对这个问题进行解答。
二、正交化的应用
谈到正交化, Q R QR QR 分解是经常一起谈论的。 Q R QR QR 分解是将一个矩阵分解为正交矩阵 Q Q Q 和上三角矩阵 R R R 的过程。很多方法可以实现这样的一个分解,上面的例子我们就使用到了施密特正交化的方法。下面是各种方法的比较:
| 方法 | 描述 | 优缺点 | 使用场景 |
|---|---|---|---|
| Gram-Schmidt过程 | 是一种迭代方法,逐列地将原始矩阵的列向量正交化 | 直观但是可能数值不稳定,尤其是当 A A A的列近似线性相关时 | 小到中型矩阵 |
| Householder变换 | 利用对称反射来逐步将矩阵变换为上三角形式的方法 | 通常比Gram-Schmidt过程更数值稳定。是许多数值线性代数库(如LAPACK)的标准方法 | 大型、满秩的密集矩阵 |
| Givens旋转 | 通过旋转来逐步零化矩阵元素,达到上三角形式 | 通常用于稀疏矩阵或特定结构的矩阵,因为可以有选择地零化矩阵的元素 | 大型、稀疏矩阵 |
| 列主元 Q R QR QR分解 | 在 Q R QR QR分解中引入列主元策略,每一步中选择“最大”的列作为下一个正交向量 | 可以提高施密特正交化过程的稳定性 | 列线性相关或者近似相关 |
施密特正交化在很多地方都有应用,这里只讨论与 Q R QR QR 有关的话题。对一个矩阵执行施密特正交化事实上就是在求取 Q R QR QR 分解中的 Q Q Q 矩阵,因为正交矩阵 Q Q Q 的特殊性,可以很轻松的通过 A A A 与正交矩阵 Q Q Q 求得 R R R 矩阵。
对于上三角矩阵,所有位于主对角线以下的元素必须为零;对于下三角矩阵,所有位于主对角线以上的元素必须为零。主对角线是否为零与是否为上下三角没有直接关系。
Q R QR QR 求解线性方程组有哪些帮助?
- 节省空间;
- 具有数值稳定性;
- 解无解方程;
我并不认为
Q
R
QR
QR 分解相对于直接求解
A
A
A 的逆有更高的效率。考虑线性方程组
A
x
=
b
Ax=b
Ax=b :
A
x
=
b
⇒
Q
R
x
=
b
⇒
R
x
=
Q
T
b
Ax=b\Rightarrow QRx=b\Rightarrow Rx=Q^Tb
Ax=b⇒QRx=b⇒Rx=QTb
令
y
=
Q
T
b
y=Q^Tb
y=QTb,有些人就下以下结论:对于不同的
b
b
b 我们只需要将其简单的乘以
Q
T
Q^T
QT 再通过回代(Back substitution)就可以得到新的方程的解,而不需要重新计算
A
−
1
A^{-1}
A−1,事实上,我们也可以通过提前计算
A
−
1
A^{-1}
A−1 来避免求逆的过程。真正有意义的是:节省存储空间。
Q
R
QR
QR 分解只需要存储一个列向量
Q
T
Q^T
QT 和上三角矩阵(有很多零,可以不存储),而后者既要存储
A
A
A,还需要存储
A
−
1
A^{-1}
A−1;
2.1 Q R QR QR 分解有更好的数值稳定性
相对于高斯消元法, Q R QR QR 分解更具有数值稳定性。数值稳定性(Numerical Stability)是指数值算法在小的扰动下(如计算机的舍去误差)下,得到的解仍然是近似于真实的解。看一个具体的例子,说明这个数值稳定性概念:
考虑系数矩阵
A
A
A 和 结果向量
b
b
b 组成的线性方程组
A
x
=
b
Ax=b
Ax=b 的解:
A
=
[
1
1
1
1.0001
]
b
=
[
2
2.0001
]
A=\begin{bmatrix}1&1\\1&1.0001\end{bmatrix} \quad b=\begin{bmatrix}2\\2.0001\end{bmatrix}
A=[1111.0001]b=[22.0001]
容易得出:
x
=
[
1
1
]
x=\begin{bmatrix}1\\1\end{bmatrix}
x=[11],当扰动作用于
b
b
b 变成
b
′
b'
b′:
b
′
=
[
2
2
]
b'=\begin{bmatrix}2\\2\end{bmatrix}
b′=[22]
这个解变成了
x
′
=
[
2
0
]
x'=\begin{bmatrix}2\\0\end{bmatrix}
x′=[20],和原来的
x
=
[
1
1
]
x=\begin{bmatrix}1\\1\end{bmatrix}
x=[11] 相差甚远,尽管我们的扰动只是
0.0001
0.0001
0.0001。为什么我们说高斯消元法的数值稳定性差呢?高斯消元法会用到某一行的倍数减去另一个行,如果乘数是基于非常小的主元计算的,乘数会非常大,所有依赖这个乘数的元素的误差都会放大,而
Q
R
QR
QR 分解的过程中,只涉及向量投影并不涉及高斯消元的小主元问题,所以我们说
Q
R
QR
QR 分解具有比高斯消元法更大的数值稳定性。
2.2 计算对称三角矩阵的全部特征值
待补充
[1] https://programmersought.com/article/41251945673/




![2023年中国煤气节能器产量及市场规模分析[图]](https://img-blog.csdnimg.cn/img_convert/b0301e3633f0d0e765597949de645b50.png)