文章目录
- 1、极值
- 2、费马引理
- 3、罗尔定理
- 4、拉格朗日中值定理
- 4.1用拉格朗日定理证明基本结论
- 5、柯西中值定理
- 6、微分中值定理的意义
- 7、三大中值定理的意义

1、极值
若
∃
δ
>
0
∃δ>0
∃δ>0,使得
∀
x
∈
U
(
x
0
,
δ
)
∀x\in U(x_0,δ)
∀x∈U(x0,δ)恒有
f
(
x
)
≥
f
(
x
0
)
,
f(x)\geq f(x_0),
f(x)≥f(x0),则称
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0取极小值
∀
x
∈
U
(
x
0
,
δ
)
∀x\in U(x_0,δ)
∀x∈U(x0,δ)恒有
f
(
x
)
≤
f
(
x
0
)
,
f(x)\leq f(x_0),
f(x)≤f(x0),则称
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0取极大值
也就是说,这一点是不是极值是根据这一点左右区间中的值决定的
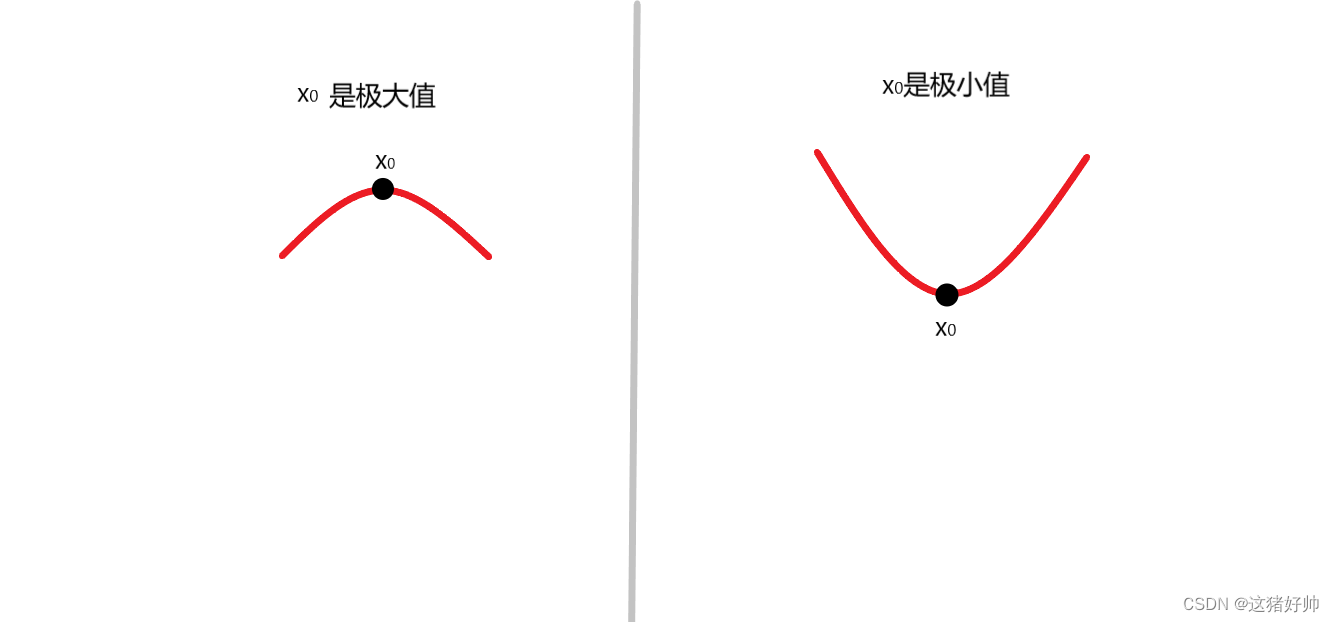
在上图中,我们在极值点做一条切线,几何上切线的斜率很明显为0
2、费马引理
若 f ( x ) f(x) f(x)在 x 0 x_0 x0处取得极值,且 f ( x ) f(x) f(x)在 x 0 x_0 x0处可导,则 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0
【证明】
不妨假设取得极大值
Δ
x
>
0
,
lim
Δ
x
→
0
+
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
=
f
+
′
(
x
)
≤
0
\Delta x>0,\lim_{\Delta x \to 0^+}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=f'_+(x)\leq 0
Δx>0,limΔx→0+Δxf(x0+Δx)−f(x0)=f+′(x)≤0
Δ
x
<
0
,
lim
Δ
x
→
0
−
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
=
f
−
′
(
x
)
≥
0
\Delta x<0,\lim_{\Delta x \to 0^-}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=f'_-(x)\geq 0
Δx<0,limΔx→0−Δxf(x0+Δx)−f(x0)=f−′(x)≥0
0
≤
f
′
(
x
0
)
≤
0
=
0
0\leq f'(x_0)\leq0=0
0≤f′(x0)≤0=0
3、罗尔定理
条件:
(1)、
f
f
f在
[
a
,
b
]
[a,b]
[a,b]上连续
(2)、
f
f
f在
(
a
,
b
)
(a,b)
(a,b)内可导
(3)、
f
(
a
)
=
f
(
b
)
f(a)=f(b)
f(a)=f(b)
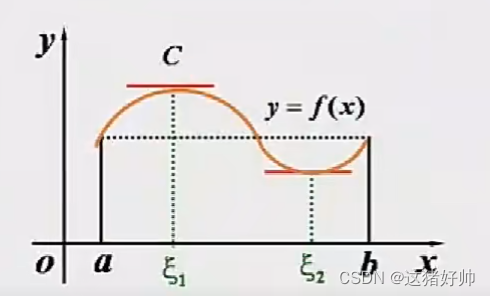
若满足上述三个条件,则
∃
ξ
∈
(
a
,
b
)
,
\exist\xi\in(a,b),
∃ξ∈(a,b),使
f
′
(
ξ
)
=
0
f'(\xi)=0
f′(ξ)=0
如图:
【证明】
∵
f
(
x
)
∵f(x)
∵f(x)在
[
a
,
b
]
[a,b]
[a,b]连续
∴
∴
∴存在最大值M与最小值m
①、若
m
=
M
⇛
f
(
x
)
=
m
=
M
,
f
′
(
x
)
=
0
m=M\Rrightarrow f(x)=m=M,f'(x)=0
m=M⇛f(x)=m=M,f′(x)=0
②、若
m
<
M
m<M
m<M且
f
(
a
)
=
f
(
b
)
f(a)=f(b)
f(a)=f(b)
则m和M至多一个在端点
不妨设
ξ
∈
(
a
,
b
)
,
f
(
ξ
)
=
m
\xi\in(a,b),f(\xi)=m
ξ∈(a,b),f(ξ)=m
f
(
x
)
≥
m
f(x)\geq m
f(x)≥m
即存在极小值
由费马引理证得:
f
′
(
ξ
)
=
0
f'(\xi)=0
f′(ξ)=0
但是,罗尔定理有一个非常特殊的要求两端点相等,在实际运用中很多时候都不能满足这个要求,人们就思考,是否能把罗尔定理进行推广,让它更具有普遍性呢?
于是数学家就发现了接下来得定理:拉格朗日中值定理
4、拉格朗日中值定理
拉格朗日的条件就是在罗尔定理的基础上把两端点相等给去掉了
条件:
(1)、
f
f
f在
[
a
,
b
]
[a,b]
[a,b]上连续
(2)、
f
f
f在
(
a
,
b
)
(a,b)
(a,b)内可导
我们连接
f
(
a
)
与
f
(
b
)
f(a)与f(b)
f(a)与f(b)做一条直线,那么至少存在一点
ξ
\xi
ξ的切线平行于这条直线
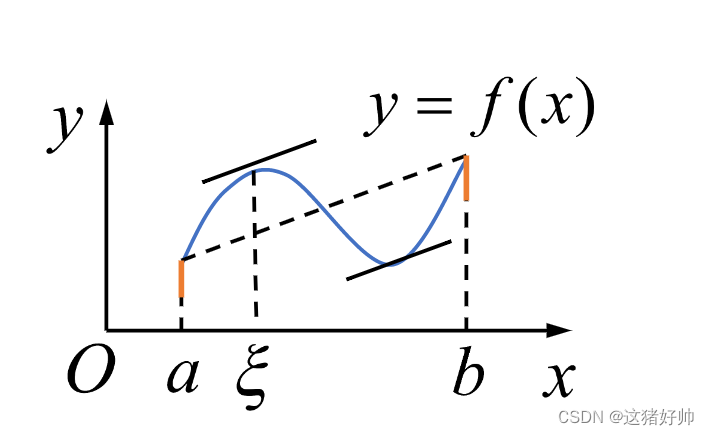
连接两端点的直线斜率:
f
(
b
)
−
f
(
a
)
b
−
a
=
f
′
(
ξ
)
⇛
f
(
b
)
−
f
(
a
)
=
f
′
(
ξ
)
(
b
−
a
)
\frac{f(b)-f(a)}{b-a}=f'(\xi)\Rrightarrow f(b)-f(a)=f'(\xi)(b-a)
b−af(b)−f(a)=f′(ξ)⇛f(b)−f(a)=f′(ξ)(b−a)
结论:若满足(1)(2),则
∃
ξ
∈
(
a
,
b
)
,
\exist \xi\in(a,b),
∃ξ∈(a,b),使
f
(
b
)
−
f
(
a
)
=
f
′
(
ξ
)
(
b
−
a
)
f(b)-f(a)=f'(\xi)(b-a)
f(b)−f(a)=f′(ξ)(b−a)
而且我们可以把这个式子改写一下:
∵
f
′
(
ξ
)
=
f
′
(
a
+
(
ξ
−
a
)
)
=
f
′
[
a
+
ξ
−
a
b
−
a
(
b
−
a
)
]
=
f
′
[
a
+
θ
(
b
−
a
)
]
(
0
<
θ
<
1
)
∵f'(\xi)=f'(a+(\xi-a))=f'[a+\frac{\xi -a}{b-a}(b-a)]=f'[a+θ(b-a)](0<θ<1)
∵f′(ξ)=f′(a+(ξ−a))=f′[a+b−aξ−a(b−a)]=f′[a+θ(b−a)](0<θ<1)
拉格朗日推论:
f
(
b
)
−
f
(
a
)
=
f
′
[
a
+
θ
(
b
−
a
)
]
(
b
−
a
)
,
(
0
<
θ
<
1
)
f(b)-f(a)=f'[a+θ(b-a)](b-a),(0<θ<1)
f(b)−f(a)=f′[a+θ(b−a)](b−a),(0<θ<1)
此时设
b
=
x
0
+
Δ
x
,
a
=
x
0
b=x_0+\Delta x,a=x_0
b=x0+Δx,a=x0
有限增量公式:
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
=
f
′
(
x
0
+
θ
Δ
x
)
Δ
x
=
Δ
y
(
0
<
θ
<
1
)
f(x_0+\Delta x)-f(x_0)=f'(x_0+θ\Delta x)\Delta x=\Delta y(0<θ<1)
f(x0+Δx)−f(x0)=f′(x0+θΔx)Δx=Δy(0<θ<1)
【证明拉格朗日定理】
f
(
b
)
−
f
(
a
)
=
f
′
(
ξ
)
(
b
−
a
)
⇛
f
′
(
ξ
)
−
f
(
b
)
−
f
(
a
)
b
−
a
=
0
f(b)-f(a)=f'(\xi)(b-a)\Rrightarrow f'(\xi)-\frac{f(b)-f(a)}{b-a}=0
f(b)−f(a)=f′(ξ)(b−a)⇛f′(ξ)−b−af(b)−f(a)=0
构造
F
(
x
)
=
f
(
x
)
−
f
(
b
)
−
f
(
a
)
b
−
a
x
F(x)=f(x)-\frac{f(b)-f(a)}{b-a}x
F(x)=f(x)−b−af(b)−f(a)x
F
(
a
)
=
f
(
a
)
−
f
(
b
)
−
f
(
a
)
b
−
a
a
=
b
f
(
a
)
−
a
f
(
a
)
−
a
f
(
b
)
+
a
f
(
a
)
b
−
a
=
b
f
(
a
)
−
a
f
(
b
)
b
−
a
F(a)=f(a)-\frac{f(b)-f(a)}{b-a}a=\frac{bf(a)-af(a)-af(b)+af(a)}{b-a}=\frac{bf(a)-af(b)}{b-a}
F(a)=f(a)−b−af(b)−f(a)a=b−abf(a)−af(a)−af(b)+af(a)=b−abf(a)−af(b)
F
(
b
)
=
f
(
b
)
−
f
(
b
)
−
f
(
a
)
b
−
a
b
=
b
f
(
b
)
−
a
f
(
b
)
−
b
f
(
b
)
+
b
f
(
a
)
b
−
a
=
b
f
(
a
)
−
a
f
(
b
)
b
−
a
F(b)=f(b)-\frac{f(b)-f(a)}{b-a}b=\frac{bf(b)-af(b)-bf(b)+bf(a)}{b-a}=\frac{bf(a)-af(b)}{b-a}
F(b)=f(b)−b−af(b)−f(a)b=b−abf(b)−af(b)−bf(b)+bf(a)=b−abf(a)−af(b)
∵
F
(
a
)
=
F
(
b
)
∵F(a)=F(b)
∵F(a)=F(b)
根据罗尔定理:
∴
F
′
(
ξ
)
=
f
′
(
ξ
)
−
f
(
b
)
−
f
(
a
)
b
−
a
=
0
⇛
f
(
b
)
−
f
(
a
)
=
f
′
(
ξ
)
(
b
−
a
)
∴F'(\xi)=f'(\xi)-\frac{f(b)-f(a)}{b-a}=0\Rrightarrow f(b)-f(a)=f'(\xi)(b-a)
∴F′(ξ)=f′(ξ)−b−af(b)−f(a)=0⇛f(b)−f(a)=f′(ξ)(b−a)
证毕
4.1用拉格朗日定理证明基本结论
推论1:设 f ( x ) f(x) f(x)在区间 I I I上连续,在 I I I内可导,则在 I I I上 f ( x ) = C ⇚ ⇛ f ′ ( x ) = 0 f(x)=C\Lleftarrow\Rrightarrow f'(x)=0 f(x)=C⇚⇛f′(x)=0
【证明】
f
(
x
)
=
C
⇚
f
′
(
x
)
=
0
f(x)=C\Lleftarrow f'(x)=0
f(x)=C⇚f′(x)=0
任取
x
1
,
x
2
∈
I
,
f
(
x
1
)
−
f
(
x
2
)
=
f
′
(
ξ
)
(
x
2
−
x
1
)
=
0
x_1,x_2\in I,f(x_1)-f(x_2)=f'(\xi)(x_2-x_1)=0
x1,x2∈I,f(x1)−f(x2)=f′(ξ)(x2−x1)=0
∴
f
′
(
x
)
=
0
⇛
f
(
x
)
=
C
∴f'(x)=0\Rrightarrow f(x)=C
∴f′(x)=0⇛f(x)=C
证毕
推论2:当 x > 0 x>0 x>0时, x 1 + x < ln ( 1 + x ) < x \frac{x}{1+x}<\ln(1+x)<x 1+xx<ln(1+x)<x
【证明】
ln
(
1
+
x
)
=
ln
(
1
+
x
)
−
ln
1
\ln(1+x)=\ln(1+x)-\ln1
ln(1+x)=ln(1+x)−ln1
ln
(
1
+
x
)
−
ln
1
=
x
ξ
(
1
<
ξ
<
1
+
x
)
\ln(1+x)-\ln1=\frac{x}{\xi}(1<\xi <1+x)
ln(1+x)−ln1=ξx(1<ξ<1+x)
令
ξ
=
1
\xi=1
ξ=1(放大):
ln
(
1
+
x
)
−
ln
1
<
x
\ln(1+x)-\ln1 <x
ln(1+x)−ln1<x
令
ξ
=
1
+
x
(
缩小
)
:
\xi=1+x(缩小):
ξ=1+x(缩小):
ln
(
1
+
x
)
−
ln
1
>
x
1
+
x
\ln(1+x)-\ln1>\frac{x}{1+x}
ln(1+x)−ln1>1+xx
故:
x
1
+
x
<
ln
(
1
+
x
)
<
x
\frac{x}{1+x}<\ln(1+x)<x
1+xx<ln(1+x)<x
证毕
5、柯西中值定理
柯西定理的思想与拉格朗日定理的思想是很像的,唯一不同的是柯西定理把求函数变成了求参数方程,
y
=
f
(
t
)
,
x
=
F
(
t
)
y=f(t),x=F(t)
y=f(t),x=F(t)
若:
(1)、
f
,
F
f,F
f,F在
[
a
,
b
]
[a,b]
[a,b]上连续
(2)、
f
,
F
f,F
f,F在
(
a
,
b
)
(a,b)
(a,b)内可导,且
∀
x
∈
(
a
,
b
)
,
F
′
(
x
)
≠
0
\forall x\in(a,b),F'(x)≠0
∀x∈(a,b),F′(x)=0
则
∃
ξ
∈
(
a
,
b
)
\exist\xi\in(a,b)
∃ξ∈(a,b),使
f
(
b
)
−
f
(
a
)
F
(
b
)
−
F
(
a
)
=
f
′
(
ξ
)
F
′
(
ξ
)
\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(\xi)}{F'(\xi)}
F(b)−F(a)f(b)−f(a)=F′(ξ)f′(ξ)
在这个结论中,左边的式子求的是连接两端点的直线斜率,右边 式子为与连接两端点的直线平行的那一点
ξ
\xi
ξ
F
′
(
x
)
≠
0
F'(x)≠0
F′(x)=0的作用:
1、保证了等式右边分母不为0
2、保证了等式左边分母不为0
因为如果左边分母为0则
F
(
b
)
=
F
(
a
)
F(b)=F(a)
F(b)=F(a),根据罗尔定理:
F
′
(
x
)
=
0
F'(x)=0
F′(x)=0,加了
F
′
(
x
)
≠
0
F'(x)≠0
F′(x)=0则限制这种情况的发生
【证明柯西中值定理】
f
(
b
)
−
f
(
a
)
F
(
b
)
−
F
(
a
)
=
f
′
(
ξ
)
F
′
(
ξ
)
⇛
[
f
(
b
)
−
f
(
a
)
]
F
′
(
ξ
)
−
[
F
(
b
)
−
F
(
a
)
]
f
′
(
ξ
)
=
0
\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(\xi)}{F'(\xi)}\Rrightarrow [f(b)-f(a)]F'(\xi)-[F(b)-F(a)]f'(\xi)=0
F(b)−F(a)f(b)−f(a)=F′(ξ)f′(ξ)⇛[f(b)−f(a)]F′(ξ)−[F(b)−F(a)]f′(ξ)=0
令
φ
(
x
)
=
[
f
(
b
)
−
f
(
a
)
]
F
(
x
)
−
[
F
(
b
)
−
F
(
a
)
]
f
(
x
)
φ(x)= [f(b)-f(a)]F(x)-[F(b)-F(a)]f(x)
φ(x)=[f(b)−f(a)]F(x)−[F(b)−F(a)]f(x)
φ
(
a
)
=
f
(
b
)
F
(
a
)
−
f
(
a
)
F
(
a
)
−
F
(
b
)
f
(
a
)
+
F
(
a
)
f
(
a
)
=
f
(
b
)
F
(
a
)
−
F
(
b
)
f
(
a
)
φ(a)=f(b)F(a)-f(a)F(a)-F(b)f(a)+F(a)f(a)=f(b)F(a)-F(b)f(a)
φ(a)=f(b)F(a)−f(a)F(a)−F(b)f(a)+F(a)f(a)=f(b)F(a)−F(b)f(a)
φ
(
b
)
=
f
(
b
)
F
(
b
)
−
f
(
a
)
F
(
b
)
−
F
(
b
)
f
(
b
)
+
F
(
a
)
f
(
b
)
=
f
(
b
)
F
(
a
)
−
F
(
b
)
f
(
a
)
φ(b)=f(b)F(b)-f(a)F(b)-F(b)f(b)+F(a)f(b)=f(b)F(a)-F(b)f(a)
φ(b)=f(b)F(b)−f(a)F(b)−F(b)f(b)+F(a)f(b)=f(b)F(a)−F(b)f(a)
φ
(
a
)
=
φ
(
b
)
φ(a)=φ(b)
φ(a)=φ(b)
根据罗尔定理:
φ
′
(
ξ
)
=
[
f
(
b
)
−
f
(
a
)
]
F
′
(
ξ
)
−
[
F
(
b
)
−
F
(
a
)
]
f
′
(
ξ
)
=
0
⇛
f
(
b
)
−
f
(
a
)
F
(
b
)
−
F
(
a
)
=
f
′
(
ξ
)
F
′
(
ξ
)
φ'(\xi)=[f(b)-f(a)]F'(\xi)-[F(b)-F(a)]f'(\xi)=0\Rrightarrow \frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(\xi)}{F'(\xi)}
φ′(ξ)=[f(b)−f(a)]F′(ξ)−[F(b)−F(a)]f′(ξ)=0⇛F(b)−F(a)f(b)−f(a)=F′(ξ)f′(ξ)
证毕
6、微分中值定理的意义
1、微分中值定理建立局部和整体的关系
我们以拉格朗日中值定理为例:
f
(
b
)
−
f
(
a
)
b
−
a
=
f
′
(
ξ
)
\frac{f(b)-f(a)}{b-a}=f'(\xi)
b−af(b)−f(a)=f′(ξ)
上述式子中,左边为
区间函数改变量
自变量改变量
\frac{区间函数改变量}{自变量改变量}
自变量改变量区间函数改变量,这是一个整体的概念
而
f
′
(
ξ
)
f'(\xi)
f′(ξ)表示的是一点上的变化率,这是一个局部的概念
而微分中值定理把这个整体和局部联系起来了
2、微分中值定理建立函数和导数的关系
7、三大中值定理的意义
柯西中值定理:
f
(
b
)
−
f
(
a
)
F
(
b
)
−
F
(
a
)
=
f
′
(
ξ
)
F
′
(
ξ
)
\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(\xi)}{F'(\xi)}
F(b)−F(a)f(b)−f(a)=F′(ξ)f′(ξ)
此时我们设
F
(
x
)
=
x
F(x)=x
F(x)=x,就得到了拉格朗日中值定理:
f
(
b
)
−
f
(
a
)
b
−
a
=
f
′
(
ξ
)
\frac{f(b)-f(a)}{b-a}=f'(\xi)
b−af(b)−f(a)=f′(ξ)
说明拉格朗日定理是柯西中值定理的特例!
如果我们令拉格朗日中值定理中的
f
(
a
)
=
f
(
b
)
f(a)=f(b)
f(a)=f(b),就得到了罗尔中值定理
f
′
(
ξ
)
=
0
f'(\xi)=0
f′(ξ)=0
说明罗尔中值定理是拉格朗日中值定理的特例!
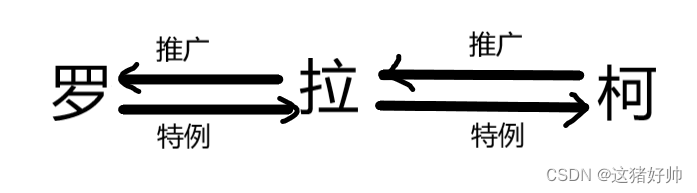

![2023年中国煤气节能器产量及市场规模分析[图]](https://img-blog.csdnimg.cn/img_convert/b0301e3633f0d0e765597949de645b50.png)











![2023年中国火焰切割机分类、产业链及市场规模分析[图]](https://img-blog.csdnimg.cn/img_convert/9b19e3bb56ecbfe0a02e94ae14245eb7.png)