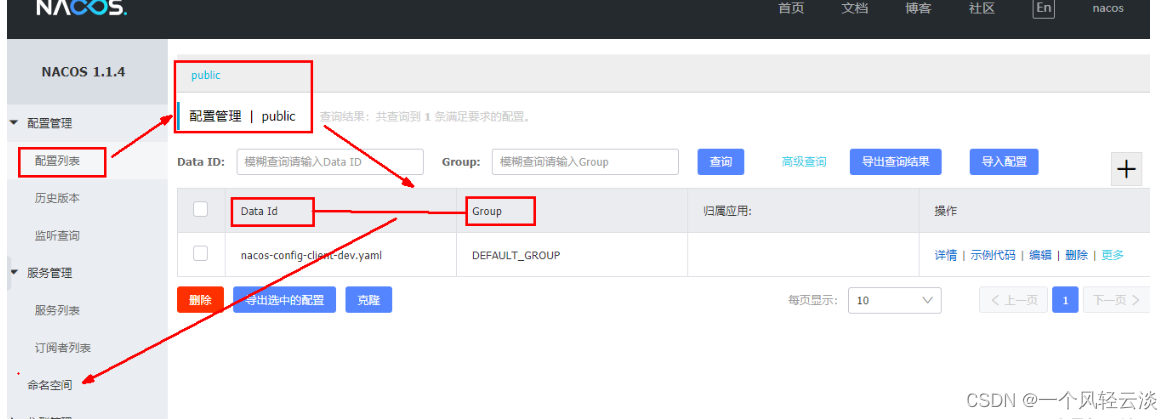
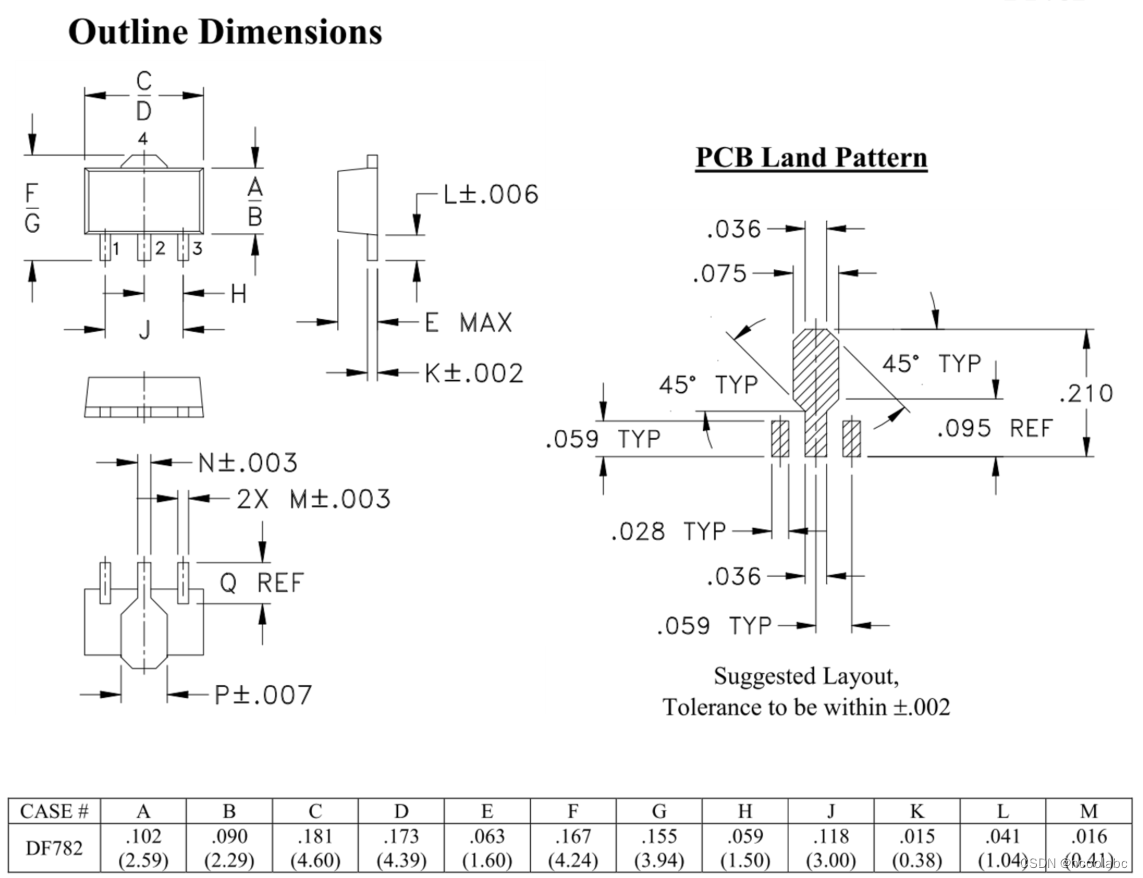
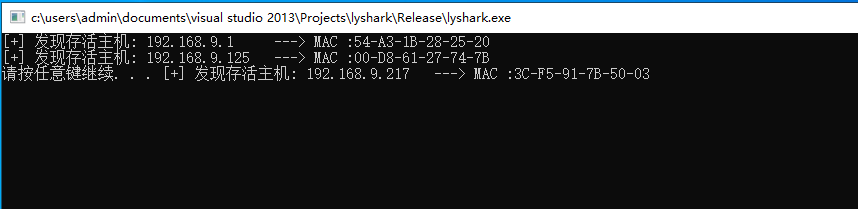
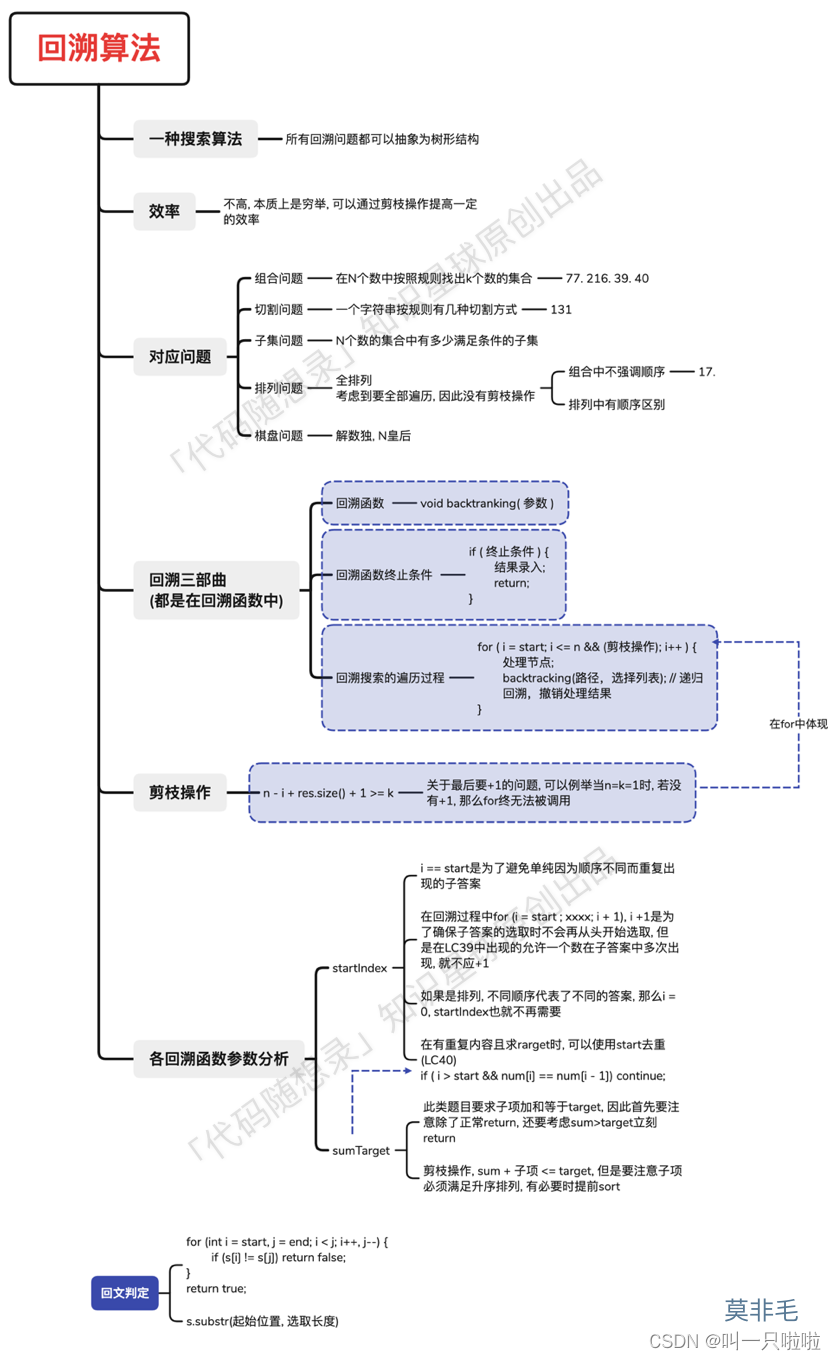
Problem - 1373D - Codeforces

 解析：

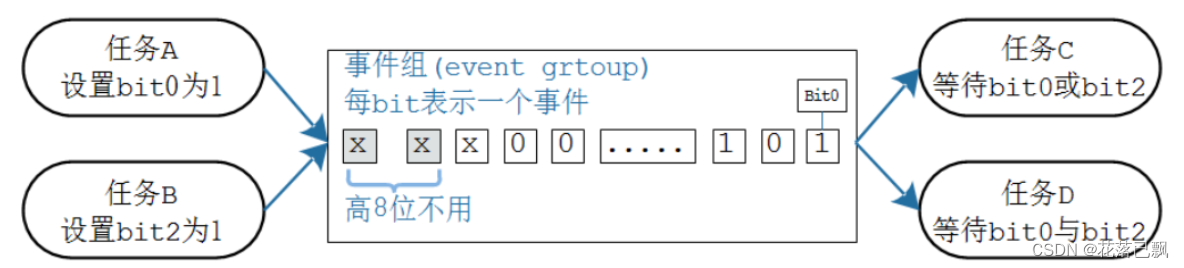
        显然可以发现，翻转数量为奇数是不影响结果，所以需要反转偶数个连续数字。

        考虑贪心，我们每次反转相邻的两个数字，并且累计贡献，如果贡献为0则清空继续累计，并且每次取贡献最大值即可。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+5;
int t,n,a[N];
signed main(){
	scanf("%lld",&t);
	while(t--){
		scanf("%lld",&n);
		int sum=0;
		for(int i=1;i<=n;i++){
			scanf("%lld",&a[i]);
			if(i%2) sum+=a[i];
		}
		int p=0,q=0,res=0;
		for(int i=1;i<=n;i++){
			if(i%2&&i<n){
				if(p<0) p=0;
				p+=a[i+1],p-=a[i];
			}
			else if(i%2==0&&i<n){
				if(q<0) q=0;
				q+=a[i],q-=a[i+1];
			}
			res=max(res,max(p,q));
		}
		printf("%lld\n\n",sum+res);
	}
	return 0;
}