回溯总结

对于回溯算法，我们需要知道的是 回溯是递归的副产品，只要有递归就会有回溯，所有回溯法常与二叉树遍历【前中后序遍历】，深搜混在一起，原因是都涉及到的递归。

回溯法 = 暴力搜索，它的效率并不高，只是我们在递归回溯的时候可以进行剪枝，减少他递归的次数与深度。

回溯算法能解决下列问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 棋盘问题：N皇后，解数独等等

回溯法对我来说还算较为容易理解，但是后面的棋盘问题，像 323.重新安排行程、51.N皇后、37.解数独 都没有什么思路，再看过一遍卡哥的视频讲解之后对于这些题脑子里面还是有些理解了，希望二刷甚至三刷的时候能够a出来，那就真的爽了，哈哈哈。

对于回溯算法，卡哥给了一个模板，基本上所有的回溯就会用到：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

组合问题

回溯算法：求组合问题！ 这是我初入回溯解决的第一道题目，卡哥在文中给我们列举了k层for循环的例子【暴力解法】，递归其实就是可以通过简短的代码实现n层for循环从而进行暴力解题的。

这题卡哥把回溯问题进行了抽象，抽象成了一个树形结构：

对于上图，我们可以很清楚的了解到：for 循环进行横向树层上的遍历，递归纵向进行树枝上的遍历，通过回溯不断调整结果集，进而收集正确的答案。

优化回溯算法 就只有剪枝这一种方法，如图：

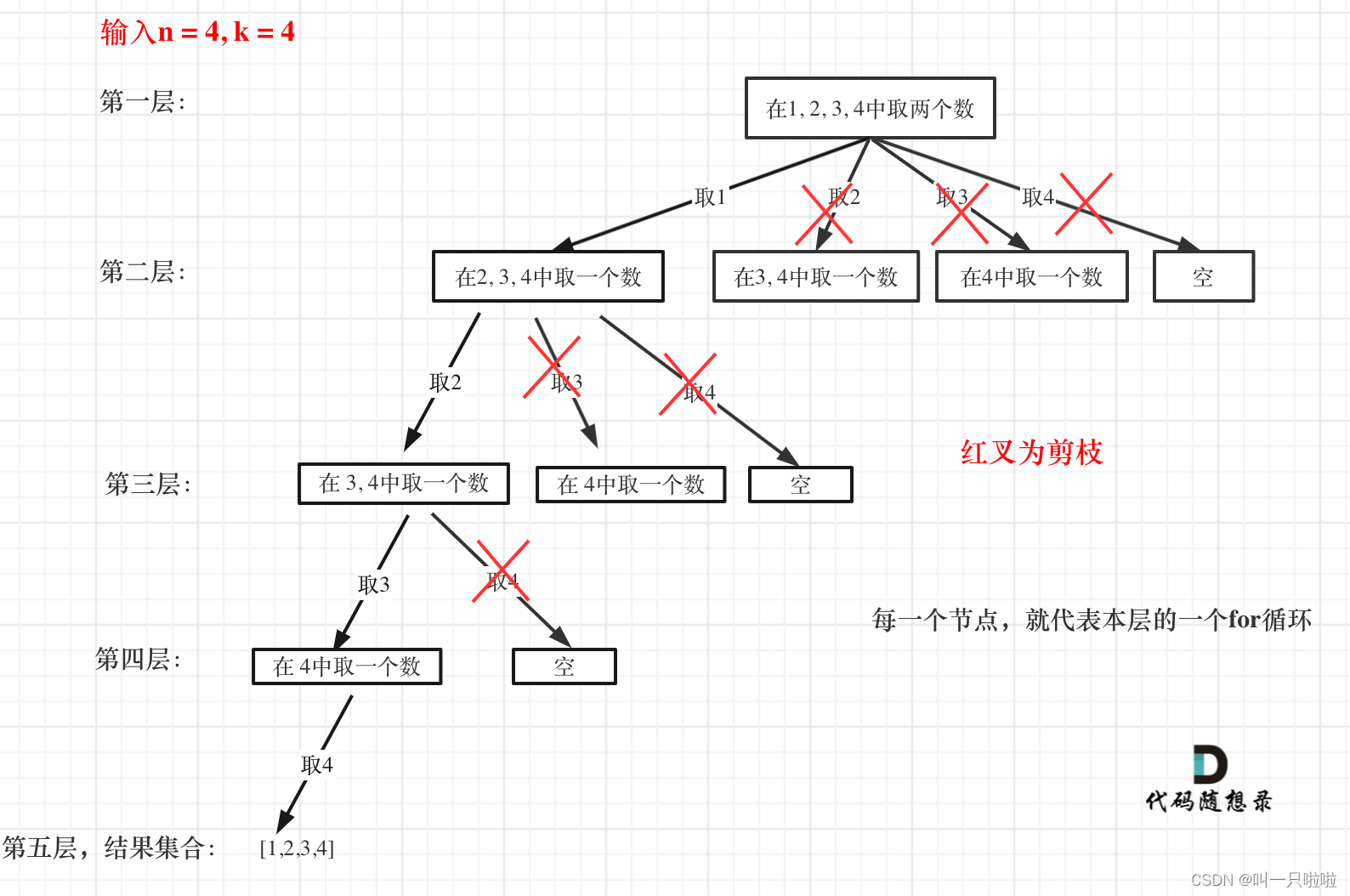
剪枝的精髓：

for循环在寻找起点的时候要有一个范围，如果这个起点到集合终止之间的元素已经不够题目要求的k个元素了，就没有必要搜索了。

切割问题

回溯算法：分割回文串 (opens new window)中，讲解切割问题，虽然最后代码看起来好像是一道模板题，但是我们从分析到学会套用这个模板，是比较难的。

如下几个难点：

• 切割问题其实类似组合问题
• 如何模拟那些切割线
• 切割问题中递归如何终止
• 在递归循环中如何截取子串
• 如何判断回文

如果想到了用求解组合问题的思路来解决 切割问题本题就成功一大半了，接下来就对着模板照葫芦画瓢。

但后序如何模拟切割线，如何终止，如何截取子串，其实都不好想，最后判断回文算是最简单的了。

除了这些难点，本题还有细节，例如：切割过的地方不能重复切割所以递归函数需要传入i + 1。

树形结构如下：

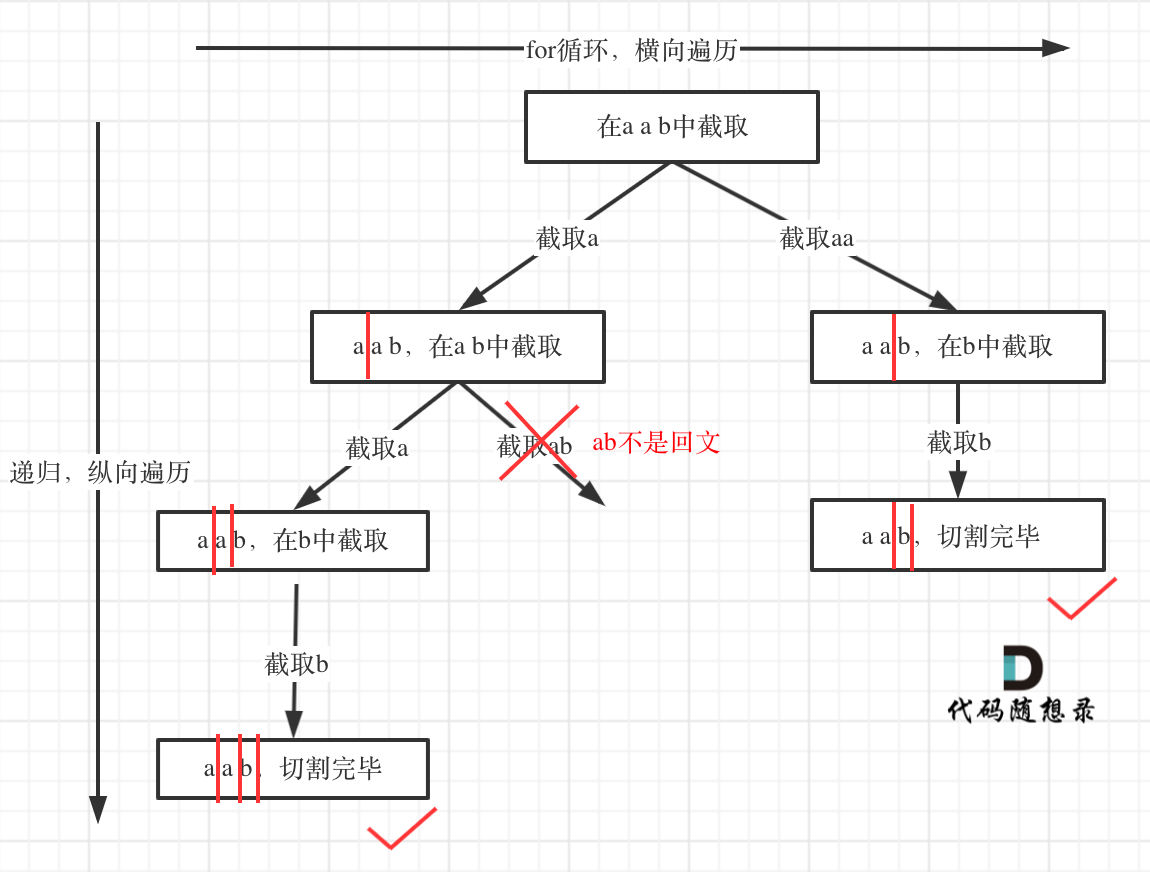
子集问题

在回溯算法：求子集问题！ (opens new window)中讲解了子集问题，在树形结构中子集问题是要收集所有节点的结果，而组合问题是收集叶子节点的结果。

如图：

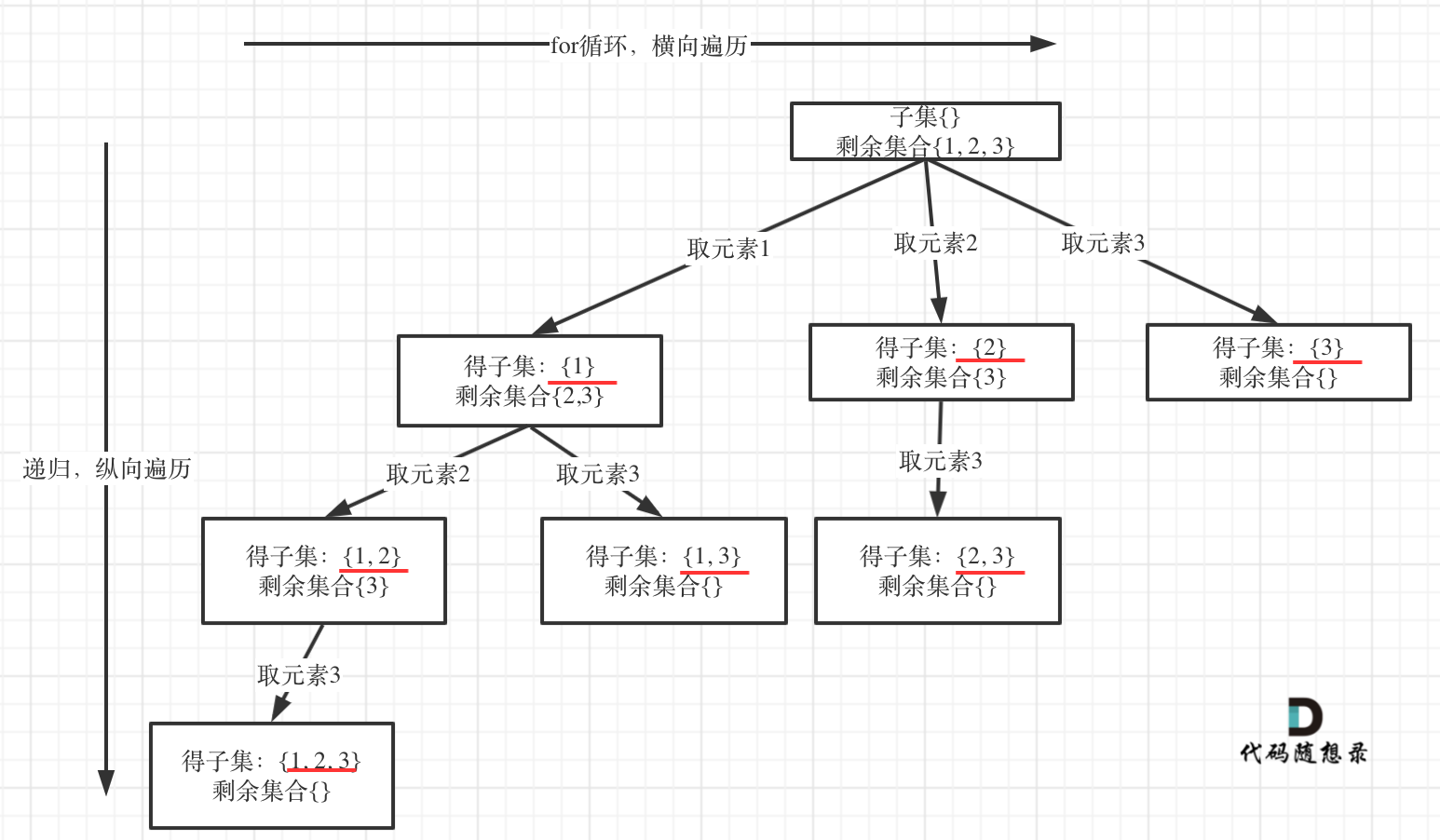
本题可以不需要加终止条件，因为startIndex >= nums.size()，本层for循环本来也结束了，因为本来我们就要遍历整棵树。

如果要写终止条件，注意：result.push_back(path);要放在终止条件的上面，如下：

result.push_back(path); // 收集子集，要放在终止添加的上面，否则会漏掉结果
if (startIndex >= nums.size()) { // 终止条件可以不加
    return;
}

排列问题

回溯算法：排列问题！ (opens new window)不一样了。

排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。

如图：

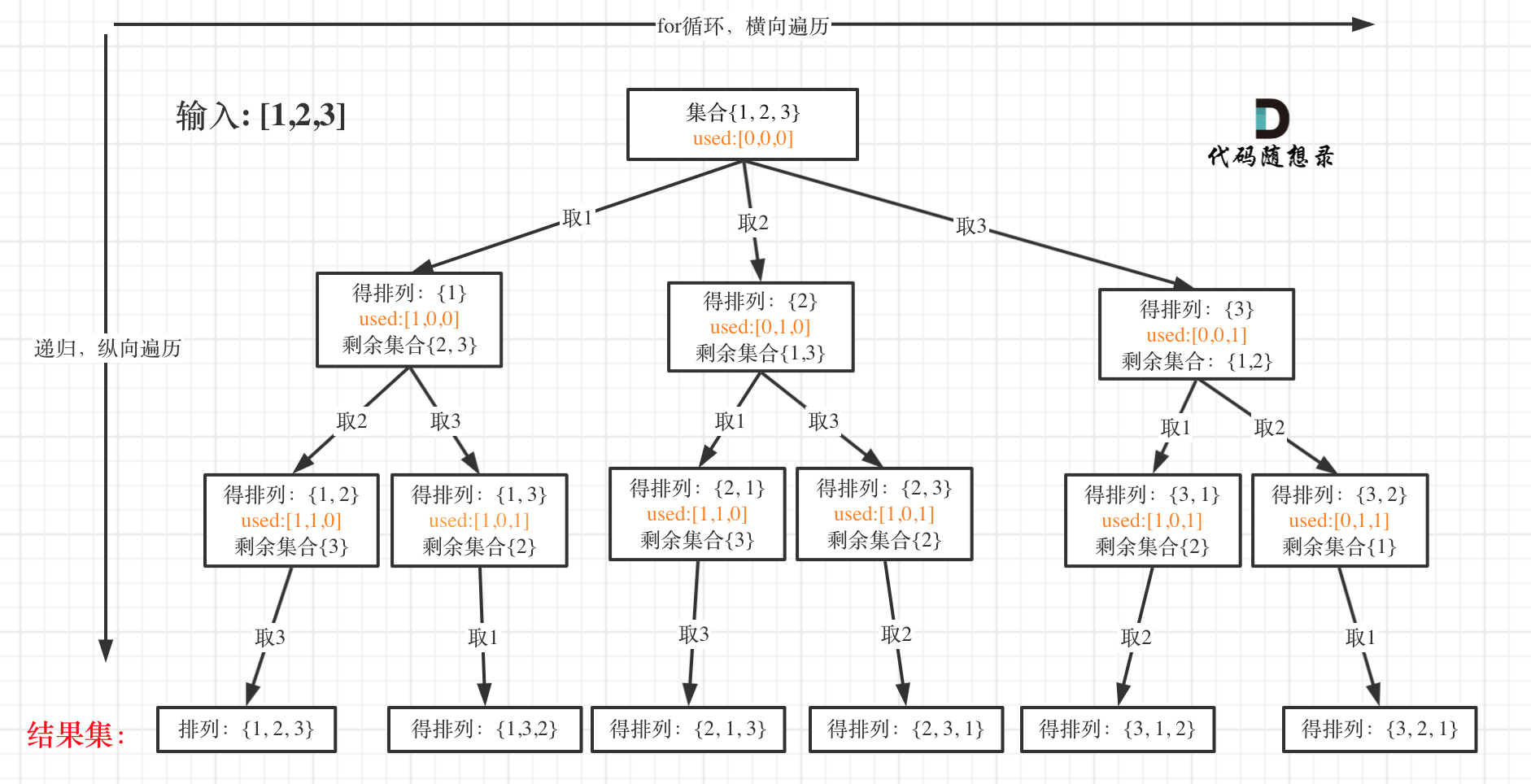
此时可以感受出排列问题的不同：

• 每层都是从0开始搜索而不是startIndex
• 需要used数组记录path里都放了哪些元素了

本题used数组即是记录path里都放了哪些元素，同时也用来去重，一举两得。

去重问题

之前都是统一使用used数组来去重的，其实使用set也可以用来去重！

在本周小结！（回溯算法系列三）续集 (opens new window)中给出了子集、组合、排列问题使用set来去重的解法以及具体代码。同时详细分析了 使用used数组去重 和 使用set去重 两种写法的性能差异：

使用set去重的版本相对于used数组的版本效率都要低很多！

原因在回溯算法：递增子序列 (opens new window)中分析过，主要是因为程序运行的时候对hashSet 频繁的add，hashSet t需要做哈希映射（也就是把key通过hash function映射为唯一的哈希值）相对费时间，而且 add 的时候其底层的符号表也要做相应的扩充，也是费时的。

而使用used数组在时间复杂度上几乎没有额外负担！

使用set去重，不仅时间复杂度高了，空间复杂度也高了，在本周小结！（回溯算法系列三） (opens new window)中分析过，组合，子集，排列问题的空间复杂度都是O(n)，但如果使用set去重，空间复杂度就变成了O(n^2)，因为每一层递归都有一个set集合，系统栈空间是n，每一个空间都有set集合。

那我们可能疑惑 用used数组也是占用O(n)的空间啊？

used数组可是全局变量，每层与每层之间公用一个used数组，所以空间复杂度是O(n + n)，最终空间复杂度还是O(n)

性能分析

【卡哥的理解】

子集问题分析：

• 时间复杂度：O(2^n)，因为每一个元素的状态无外乎取与不取，所以时间复杂度为O(2^n)
• 空间复杂度：O(n)，递归深度为n，所以系统栈所用空间为O(n)，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为O(n)

排列问题分析：

• 时间复杂度：O(n!)，这个可以从排列的树形图中很明显发现，每一层节点为n，第二层每一个分支都延伸了n-1个分支，再往下又是n-2个分支，所以一直到叶子节点一共就是 n * n-1 * n-2 * ..... 1 = n!。
• 空间复杂度：O(n)，和子集问题同理。

组合问题分析：

• 时间复杂度：O(2^n)，组合问题其实就是一种子集的问题，所以组合问题最坏的情况，也不会超过子集问题的时间复杂度。
• 空间复杂度：O(n)，和子集问题同理。

N皇后问题分析：

• 时间复杂度：O(n!) ，其实如果看树形图的话，直觉上是O(n^n)，但皇后之间不能见面所以在搜索的过程中是有剪枝的，最差也就是O（n!），n!表示n * (n-1) * .... * 1。
• 空间复杂度：O(n)，和子集问题同理。

解数独问题分析：

• 时间复杂度：O(9^m) , m是'.'的数目。
• 空间复杂度：O(n^2)，递归的深度是n^2

一般说道回溯算法的复杂度，都说是指数级别的时间复杂度，这也算是一个概括吧！

回溯专题汇聚为一张图：

---

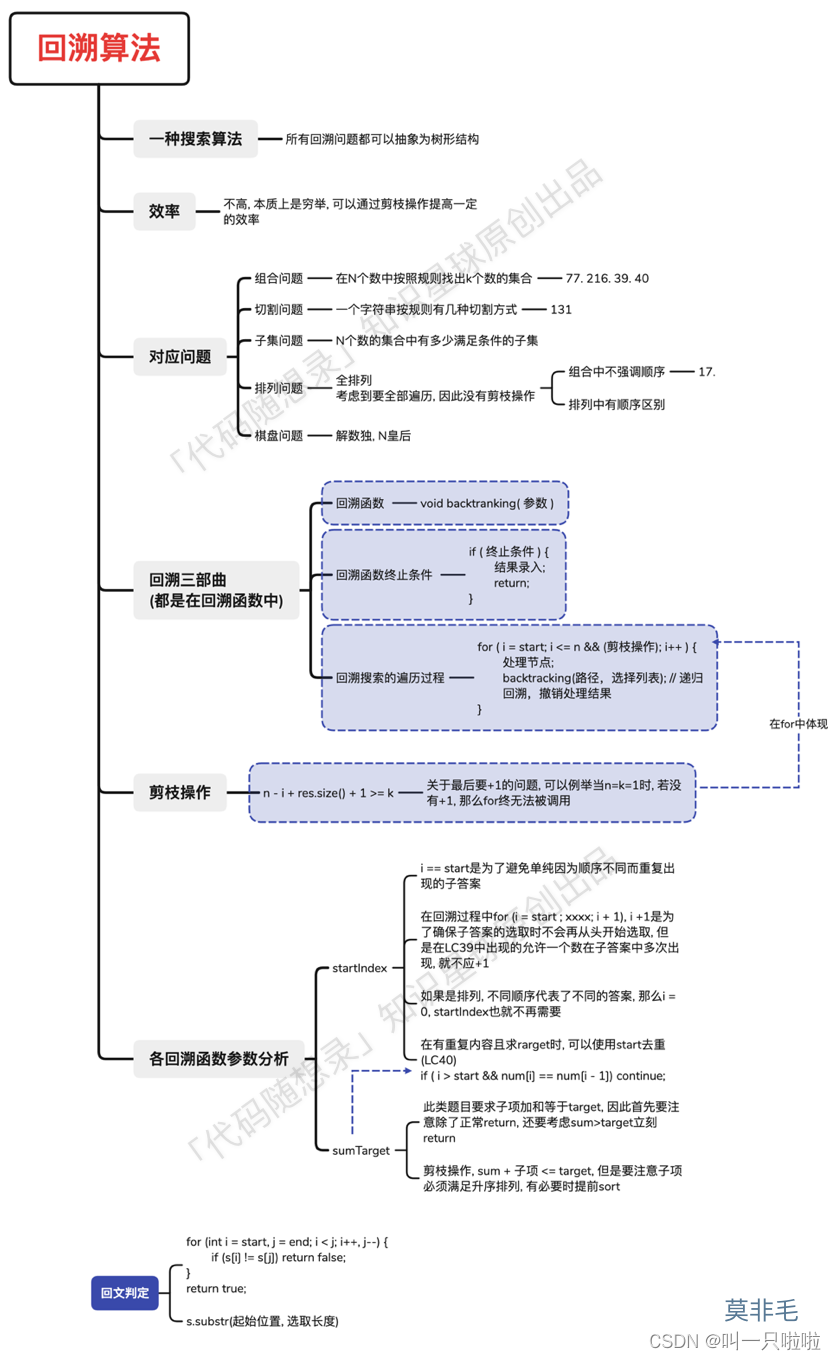
上述是根据卡哥的总结及自己的一些了解的综合，自己的语言组织能力较弱，很多都是直接抄卡哥的，有错误望指正。