位图是一种较难理解的数据结构,想了解位图,我需要先温习一下基础,复习下一些二进制的知识
位运算
1个字节=8个二进制位
二进制每逢二进一,下面是二进制对应的十进制转换方式
| 二进制 | 十进制 |
|---|---|
| 0000 0001 | 2^0=1 |
| 0000 0010 | 2^1=2 |
| 0000 0011 | 21+20=3 |
左移
每个二进制位都向左移动一位
1 << 1
移动前
0000 0001
移动后
0000 0010
右移
每个二进制位都向右移动一位
1 >> 1
移动前
0000 0001
移动后
0000 0000
与运算
两个位都是1,结果为1。否则为0
0000 0010
&0000 0011
=
0000 0010
或运算
两个位都是0,结果为0。否则为1
0000 0010
|0000 0011
=
0000 0011
位图
位图的思想用利用每个二进制位的值来存储数据,优点是可以极大的节省空间
我们举个例子。有 1 千万个整数,整数的范围在 1 到 1 亿之间。如何快速查找某个整数是否在这 1 千万个整数中呢?
我们需要存储1000w个整数范围1-1亿之前的整数,用做已经使用过的数据。那么我们会选择怎么存储?我们可以使用hashSet来存储着1000w个数据,但是这样这个hashSet占据了4byte*1000w=40mb
我们试试用位图,假设我们用一亿个二进制位的数组表示位图,然后把每个数字放入位图。怎么放入呢,比如我们要放入4这个整数,那个我们就把数组第4个下标的值设置成1,以此类推。当我们要判断4是否存在,那么我们只需要取出下标为4的值判断是否为1,为1则存在了。
例如 [0,0,0,0,1,1,0,0],表示位图存储了2和3两个整数,这样我们只需要1亿个bit=12mb的内存
我们还可以用另一个存储结构来使用位图
我们举一个场景,订单有各种异常状态,大概有几十个。如果我们把订单的各种异常都存储成各个字段的话,那么整个订单表异常的字段会变得非常多。
我们可以使用一个long型运用位图的思想来存储。首先我们先约定各个异常对应的位图的位置,比如缺货异常是1,退款异常是2。如果一个订单标记了缺货和退款两个异常,那我们怎么来存储。首先没有异常情况是,这个字段二进制是0000(简写了,实际是64个二进制位),
这里有个数学公式,我们想要在第n位上标记成1,我们可以使用或运算 原值 | (1<<n) 的公式
然后我们需要标记缺货异常,只需要0|1<<1
00000 | 0010 = 0010
(既 0 | 1<<1 = 0 | 2 = 2)
这样第一个位置就变成1了,然后我们要标记退款异常,
0010 | 0100 = 0110
(既 2 | 1<<2 = 2 | 4 = 6)
这样第二个位置也变成了1
这样我们在订单表只需要存储一个字段,并存储为6就可以了
这样存储怎么查询呢,如果我要查询有缺货异常的订单。我们已知缺货异常对应的二进制位数是1,我们只需要使用与运算
例如
0110 && 0010 = 0010 (既 6&(1<<1)= 2)大于0则表示第一位是1,既有缺货异常
0100 && 0010 = 0000 (既 4&(1<<1)= 0)=0表示第一位是0,既没有缺货异常
进阶:布隆过滤器
我们会发现位图的大小会随着范围的变大而变大,回到之前的题目,如果有 1 千万个整数,整数的范围在 1 到 1 0亿之间。如何快速查找某个整数是否在这 1 千万个整数中呢?
如果我们在使用位图就会发现我们需要使用一个10亿的二进制位来存储,那么则需要120mb的内存,内存占用反而比hashSet还要大。那么我们应该怎么办呢?
不知道大家有没有了解过布隆过滤器这个数据结构。布隆过滤器正是为了解决上述的问题,它是位图的一种改进版。
我们仍仅使用1亿个二进制位数组作为存储结构,然后对存储的值进行hash运算,运算后再对位图的大小进行取模,将对应位置设置为1。如果只有一个hash函数,那么冲突的概率还是很大的,比如1和1亿零1 对1亿取模都等于1,所以布隆过滤器会进行多个hash函数取模运算,并将这些位置都设置为1。经过多个hash函数的运算,hash冲突的概率会小很多。
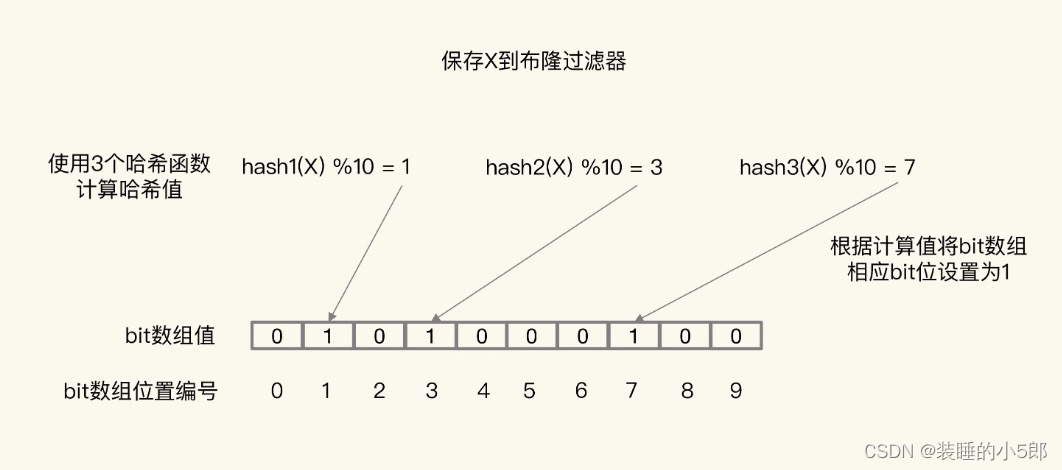
布隆过滤器会存在一定的误判率,当我们判断某个整数是否在这 1 千万个整数中,同样会对这个数字进行多次hash取模运算,如果这些位置上都是1,那么可以判断这个整数可能存在。如果这些位置上有0,但是可以判断这个整数肯定不存在