前言

        大家好~~~~呀！很荣幸你能点击这篇文章。本篇也是我的一份学习笔记，让我们一起共同成长吧~ing......

C++红黑树的简单插入实现博客~

【C++】红黑树的插入实现_柒海啦的博客-CSDN博客

二叉搜索树的基本结构和实现博客~

【C++】二叉搜索树_柒海啦的博客-CSDN博客_c++二叉搜索树

        本篇笔记基于红黑树的基本插入实现，实现简单的map和set的包装，掌握底层的基本原理即可~

 （嘿嘿玉子阔爱~~~）

目录

前言

一、map和set的基本使用

1.set的使用

1.1set的模板参数：

1.2set的迭代器：

1.3set的修改：

1.4set的操作：

1.5代码测试：

2.map的使用

2.1map的模板参数：

2.2map的迭代器：

2.3map的修改：

2.4map的操作： 

2.5代码操作：

二、基于插入实现的红黑树进行封装

1.优化红黑树的模板参数

上层代码初步实现：

下层红黑树代码：

 2.红黑树的迭代器实现

重载++/--运算符：

3.map、set上层对红黑树迭代器的相关封装：

4.mapset综合简单封装代码：

---

一、map和set的基本使用

        在一开始，我们接触的C++STL容器比如：vector、list、stack、deque....这些容器的底层都是为线性序列的数据结构，存储的就是元素本身。这些就是序列式容器。

        除了序列式容器外，还有关联式容器。它也是存储数据的，只不过和序列式容器不同的是内部存储的是key-value结构的键值对，并且数据结构也是非线性的（二叉树）。而现在我们要介绍的map和set均为关联式容器。

1.set的使用

set文档：set - C++ Reference (cplusplus.com)

multiset文档：multiset - C++ Reference (cplusplus.com)

1.set是按照一定顺序进行存储的容器。

2.set/multiset 底层数据均是<key, key>的键值对。插入只需要一个key类型即可。

3.set的元素不可重复，multiset的元素可重复。

4.使用set的迭代器进行遍历可以得到有序序列。

5.set的元素默认按照小于来比较，查找某个元素时间复杂度为log_2 N，并且元素不可修改。

6.底层使用二叉搜索树-红黑树进行实现。

（注：下述以set为准，multiset使用接口类似）

1.1set的模板参数：

T -  插入元素的数据类型。

Compare - 比较仿函数。默认给的less为库中实现的小于比较。

Alloc - 内存分配

（上述模板在模拟实现中目前只关注T）

1.2set的迭代器：

（解引用返回的就是T这个元素类型） 

1.3set的修改：

insert -  插入T类型的元素，或者在一段迭代器区间进行插入（模拟实现只实现第一种） erase - 删除对应迭代器指向元素，或者一段迭代器区间的元素（模拟实现只实现第一种）

1.4set的操作：

find - 根据传入的元素返回一个迭代器。没有找到返回的就是end()。

count - 根据传入的元素返回其出现的个数（对于multiset有效）

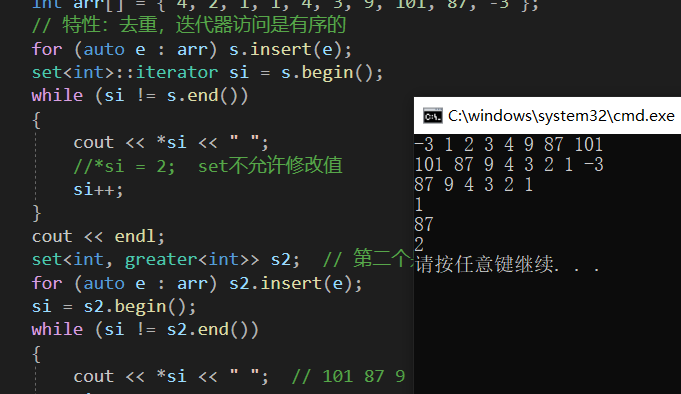
1.5代码测试：

void test2()
{
	//set的使用 - 底层使用的是红黑树进行封装的
	set<int> s;
	int arr[] = { 4, 2, 1, 1, 4, 3, 9, 101, 87, -3 };
	// 特性：去重，迭代器访问是有序的
	for (auto e : arr) s.insert(e);
	set<int>::iterator si = s.begin();
	while (si != s.end())
	{
		cout << *si << " ";
		//*si = 2;  set不允许修改值
		si++;
	}
	cout << endl;
	set<int, greater<int>> s2;  // 第二个是配置的仿函数 - 给其底层对应key的比较大小
	for (auto e : arr) s2.insert(e);
	si = s2.begin();
	while (si != s2.end())
	{
		cout << *si << " ";  // 101 87 9 4 3 2 1 -3
		si++;
	}
	cout << endl;
	// 可删除
	s2.erase(-3);
	s2.erase(s2.begin());
	si = s2.begin();
	while (si != s2.end())
	{
		cout << *si << " ";  // 87 9 4 3 2 1
		si++;
	}
	cout << endl;
	cout << s2.count(4) << endl;  // 返回对应个数 -- 对于不可冗余的set没啥用
	// 查找，返回迭代器 set具有const，无法修改
	cout << *s2.find(87) << endl;
	//cout << *s2.find(10) << endl;  // 返回的是end
	multiset<int> ms(arr, arr + (sizeof(arr) / sizeof(arr[0])));  // 可以使用迭代器构造 - 使用的是multi 可以重复的使用元素哦~
	cout << ms.count(4) << endl;  // 2
}

运行结果： 

2.map的使用

map文档：map - C++ Reference (cplusplus.com)

multimap文档：multimap - C++ Reference (cplusplus.com)

1. map是关联容器，它按照特定的次序(按照key来比较)存储由键值key和值value组合而成的元素（pair）。

2.同样的默认小于进行比较，比较的元素也key类型的元素。查找类型同样是key，时间复杂度也是log_2 N。并且key不可修改，但是对应的value可以进行修改。

3.针对于key元素，利用迭代器遍历可以得到有序序列。

4.支持[]进行访问。

5.map的key不可重复，multimap的key允许重复。

6.底层使用二叉搜索树-红黑树进行实现。

（注：下述以map为准，multimap使用接口类似）

2.1map的模板参数：

Key、T - 对应键值对中的key-value。之后插入比较均以key类型元素为基准。

Compare - 比较仿函数。默认给的less为库中实现的小于比较。

Alloc - 内存分配

2.2map的迭代器：

 （此时返回的迭代器类型解用引用后是个pair<Key, T>元素）

2.3map的修改：

operator[] - 

访问对应key下标的value值。如果key不存在，那么就进行新的插入，返回值为以T类型调用的默认构造。

at - 访问key下标对应的value值。如果key不存在，则抛异常。

insert - 

 erase - 

2.4map的操作： 

find - 根据传入的元素返回一个迭代器。没有找到返回的就是end()。

count - 根据传入的key返回其出现的对数（对于multimap有效）

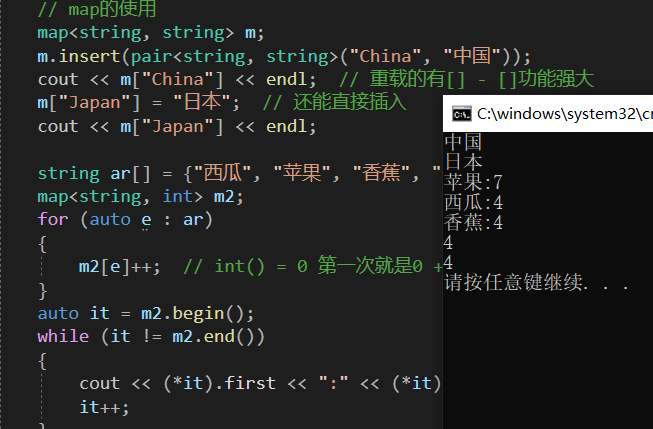
2.5代码操作：

void test3()
{
	// map的使用
	map<string, string> m;
	m.insert(pair<string, string>("China", "中国"));
	cout << m["China"] << endl;  // 重载的有[] - []功能强大
	m["Japan"] = "日本";  // 还能直接插入
	cout << m["Japan"] << endl;

	string ar[] = {"西瓜", "苹果", "香蕉", "香蕉", "苹果", "西瓜", "苹果", "香蕉", "西瓜", "苹果", "苹果", "苹果", "西瓜", "苹果", "香蕉"};
	map<string, int> m2;
	for (auto e : ar)
	{
		m2[e]++;  // int() = 0 第一次就是0 + 1 = 1， 存在就++
	}
	auto it = m2.begin();
	while (it != m2.end())
	{
		cout << (*it).first << ":" << (*it).second << endl;
		it++;
	}
	cout << (*m2.find("西瓜")).second << endl;  // 同样的返回迭代器
	cout << m2.find("西瓜")->second << endl;  // 同样的返回迭代器
}

运行结果： 

 

二、基于插入实现的红黑树进行封装

        在了解了基本map和set的基本使用后，我们可以利用之前实现的简单插入实现的红黑树进行封装，文章链接在前言哦~

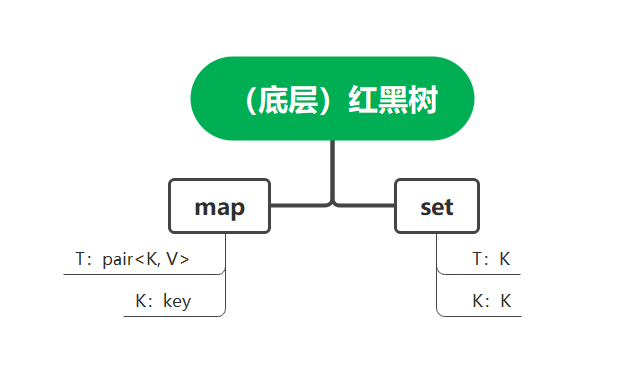
1.优化红黑树的模板参数

        首先，因为我们实现的红黑树利用的K-Value模型。为了兼容set和map的存储结构（一个只是value、一个是key - value），我们就保留K这个模板参数，利用T这个模板参数一个存储value、一个存储pair<Key, value>。

        那么此时插入数据就是T类型的数据。由于是上层封装，所以传到红黑树这一层，就不知道T类型究竟是value还是一个键值对。此时同样需要上层传入一个仿函数，每次控制对应类型取出对应的key值。set key就是本身，map pair<key, value>->frist。

上层代码初步实现：

map:

namespace YuShen
{
	template<class K, class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)  // 重载()
			{
				return kv.first;
			}
		};
	public:
    // ......
	private:
		RBTree<K, pair<K, V>, MapKeyOfT> _t; // 红黑树结构
	};
}

set：

namespace YuShen
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};

	public:
    // ......
	private:
		RBTree<K, K, SetKeyOfT> _t;
	};
}

下层红黑树代码：

template<class K, class T, class KeyOfT>
class RBTree
{
	typedef RBTreeNode<T> Node;
    // .......
};

// 红黑树结点结构
template<class T>
struct RBTreeNode
{
    //......
};

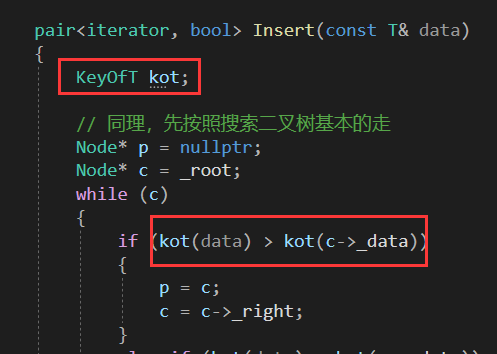
        此时原本的红黑树key和value模型就混在一起了，需要将所有需要取出key的地方（比如比较的地方）都要利用传入的仿函数对象进行比较，比如：

 2.红黑树的迭代器实现

        在上述的使用中，我们发现map和set都是可以控制迭代器的。实际上，它们调用的就是底层红黑树自己实现的迭代器。

        此时迭代器也就需要自己实现了。首先红黑树是一个二叉树结构，非线性结构，和list的模拟实现类似。

        其次红黑树是一个二叉搜索树。因为控制了所以结点值大于对应结点的左子树的值，小于对应结点的右子树的值的性质，所以对二叉搜索树来说，中序遍历是有序的。那么在接下来的迭代器实现中++或者--就要按照中序的性质进行实现：

红黑树迭代器简单实现：-模板类

模板参数：（STL迭代器三样）class T, class Ref, class Ptr （T T& T*）

重载运算符：

        *解引用        ->箭头访问（指针）        ==/!=        ++ --

解引用、箭头访问、== !=的简单实现：

template<class T, class Ref, class Ptr>  // T T& T*
struct __RBTreeIterator
{
	RBTreeNode<T>* node;
	typedef __RBTreeIterator<T, Ref, Ptr> Self;

	__RBTreeIterator(RBTreeNode<T>* root)
		:node(root)
	{}
	Ref operator*()
	{
		return node->_data;
	}

	Ptr operator->()
	{
		return &node->_data;
	}

	bool operator==(const Self& it) const
	{
		return it.node == node;
	}

	bool operator!=(const Self& it) const
	{
		return it.node != node;
	}
    // ..... ..

}

重载++/--运算符：

        由于实现红黑树的迭代器，当前迭代器存储的结点，要让它指向++后也就是中序的下一个。我们想想中序的时候是如何进行遍历的？左子树，当前结点，右子树。所以，当到此结点后，表示此结点的左子树已经遍历过了，我们就遍历到右子树即可。

        到右子树就要找到右子树中的最左的结点。但是，如果右子树为空呢？按照之前的中序递归方式，此时就会返回到上一层也就是父节点的地方。但是以下面的的一张图为例，有着两种不同的情况：

 

        如果当前结点为1，那么++后就是3结点。 但是如果当前结点为4的话，那么++后的结点就应该是5结点。此时找的条件就是孩子不是父右子树的节点。一直找到空表示此时中序遍历到空了。

        -- 是完全反过来的，首先当前结点，那么右子树已经遍历过了，此时找到左子树的最右结点。如果为空，那么就找到孩子不是父左子树的结点即可。

简单代码实现：

	Self& operator++()
	{
		// 中序访问-只不过是碎片化的进行访问
		if (node->_right)
		{
			// 找到右子树最左结点 -- 
			node = node->_right;
			while (node->_left) node = node->_left;
		}
		else
		{
			// 右子树为空，直接访问父节点吗？不一定哦，需要向上找孩子不是父亲的右结点的那个祖先
			RBTreeNode<T>* parent = node->_parent;
			while (parent && parent->_right == node)
			{
				node = parent;
				parent = node->_parent;
			}
			node = parent;
		}
		return *this;
	}

	Self& operator--()  // 反过来了
	{
		if (node->_left)
		{
			node = node->_left;
			while (node->_right) node = node->_right;
		}
		else
		{
			// 右子树为空，直接访问父节点吗？不一定哦，需要向上找孩子不是父亲的右结点的那个祖先
			RBTreeNode<T>* parent = node->_parent;
			while (parent && parent->_left == node)
			{
				node = parent;
				parent = node->_parent;
			}
			node = parent;
		}
		return *this;
	}

3.map、set上层对红黑树迭代器的相关封装：

        在实现了红黑树的迭代器后，就可以具体写出begin和end了，begin就当前红黑树存储的根结点。end只需要给一个空结点过去即可。

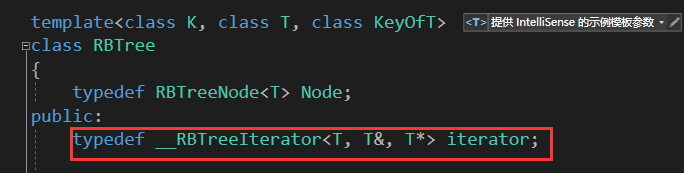
         map和set首先对此红黑树类型中的iterator类型进行重命名。由于是通过域访问符::进行访问的，所以编译器编译的时候不好判断其究竟是静态变量还是类型，所以类型的前面就需要加上typename表示这是一个类型以保证编译过的去：

// map		
    typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;
// set
    typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;

        那么对于插入insert，我们的返回值可以是一个pair，里面存放迭代器和一个bool值。插入失败就返回对应元素的迭代器和false，插入成功就返回插入新结点的迭代器和true值。

		pair<iterator, bool>insert(const K& key)
		{
			return _t.Insert(key);
		}

        对于map来说，此结构还可以方便我们实现[]重载。因为在之前的使用中，我们发现对于map的[]，如果对应key数据存在就返回其对应的value值，如果不存在就会创建新的键值对。实际上就是在调用[]调用红黑树的inset，传入key和利用其V的默认构造进行插入，传入失败就说明存在元素，然后返回对应的迭代器的value值即可，插入成功同样返回迭代器的value值即可：

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = _t.Insert(pair<K, V>(key, V()));
			return ret.first->second;
		}

        find同样的类似实现，返回迭代器即可。

4.mapset综合简单封装代码：

// map.h
#pragma once
#include "RBTree.h"

// 利用自己实现的红黑树去封装map
// 实验基本功能：数据不冗余，基本实现insert、[]等功能 
namespace YuShen
{
	template<class K, class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)  // 重载()
			{
				return kv.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}
		iterator end()
		{
			return _t.end();
		}
		pair<iterator, bool> insert(const pair<K, V>& kv)
		{
			return _t.Insert(kv);
		}

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = _t.Insert(pair<K, V>(key, V()));
			return ret.first->second;
		}

		iterator find(const K& key)
		{
			return _t.find(key);
		}
	private:
		RBTree<K, pair<K, V>, MapKeyOfT> _t; // 红黑树结构
	};
}

// set.h
#pragma once

namespace YuShen
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};

	public:
		typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;

		pair<iterator, bool>insert(const K& key)
		{
			return _t.Insert(key);
		}

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		iterator find(const K& key)
		{
			return _t.find(key);
		}
	private:
		RBTree<K, K, SetKeyOfT> _t;
	};
}

另外，加上红黑树中的find实现：

	iterator find(const K& key)
	{
		Node* tmp = _root;
		KeyOfT kot;
		while (tmp)
		{
			if (key > kot(tmp->_data)) tmp = tmp->_right;
			else if (key < kot(tmp->_data)) tmp = tmp->_left;
			else return iterator(tmp);
		}
		return iterator(nullptr);
	}