Opencv之RANSAC算法用于直线拟合及特征点集匹配详解
-
- 讲述Ransac拟合与最小二乘在曲线拟合上的优缺点
-
- 讲述在进行特征点匹配时,最近邻匹配与Ransac匹配的不同之处
-
- 另外,Ransac也被用于椭圆拟合、变换矩阵求解等
1. 直线拟合
1.1 原理
-
RANSAC(RANdom SAmple Consensus,随机采样一致)算法是从一组含有“外点”(outliers)的数据中正确估计数学模型参数的迭代算法。“外点”一般指的的数据中的噪声,比如说匹配中的误匹配和估计曲线中的离群点。故RANSAC也是一种“外点”检测算法。同时RANSAC是一个非确定性算法,在某种意义上说,它会产生一个在一定概率下合理的结果,其允许使用更多次的迭代来使其概率增加。
-
RANSAC算最早是由Fischler和Bolles在SRI上提出用来解决LDP(Location Determination Problem,位置确定问题)问题的。
-
对于RANSAC算法来说一个基本的假设就是数据是由“内点”和“外点”组成的。“内点”就是组成模型参数的数据,“外点”就是不适合模型的数据。同时RANSAC假设:在给定一组含有少部分“内点”的数据,存在一个程序可以估计出符合“内点”的模型
-
算法主要思想:
- 给定一个数据集S,从中选择建立模型所需的最小样本数(空间直线最少可以由两个点确定,所以最小样本数是2,空间平面可以根据不共线三点确定,所以最小样本数为3,拟一个圆时,最小样本数是3),记选择数据集为S1
使用选择的数据集S1计算得到一个数学模型M1- 用计算的模型M1去测试数据集中剩余的点,如果测试的数据点在误差允许的范围内,则将该数据点判为内点(inlier),否则判为外点(outlier),记所有内点组成的数据集为S1*,S1* 称作 S1的一致性集合
- 比较当前模型和之前推出的最好的模型的“内点”的数量,记录最大“内点”数量时模型参数和“内点”数量
- 重复1-4步,直到迭代结束或者当前模型已经足够好了(“内点数目大于设定的阈值”);每次产生的模型要么因为内点太少而被舍弃,要么因为比现有的模型更好而被选用
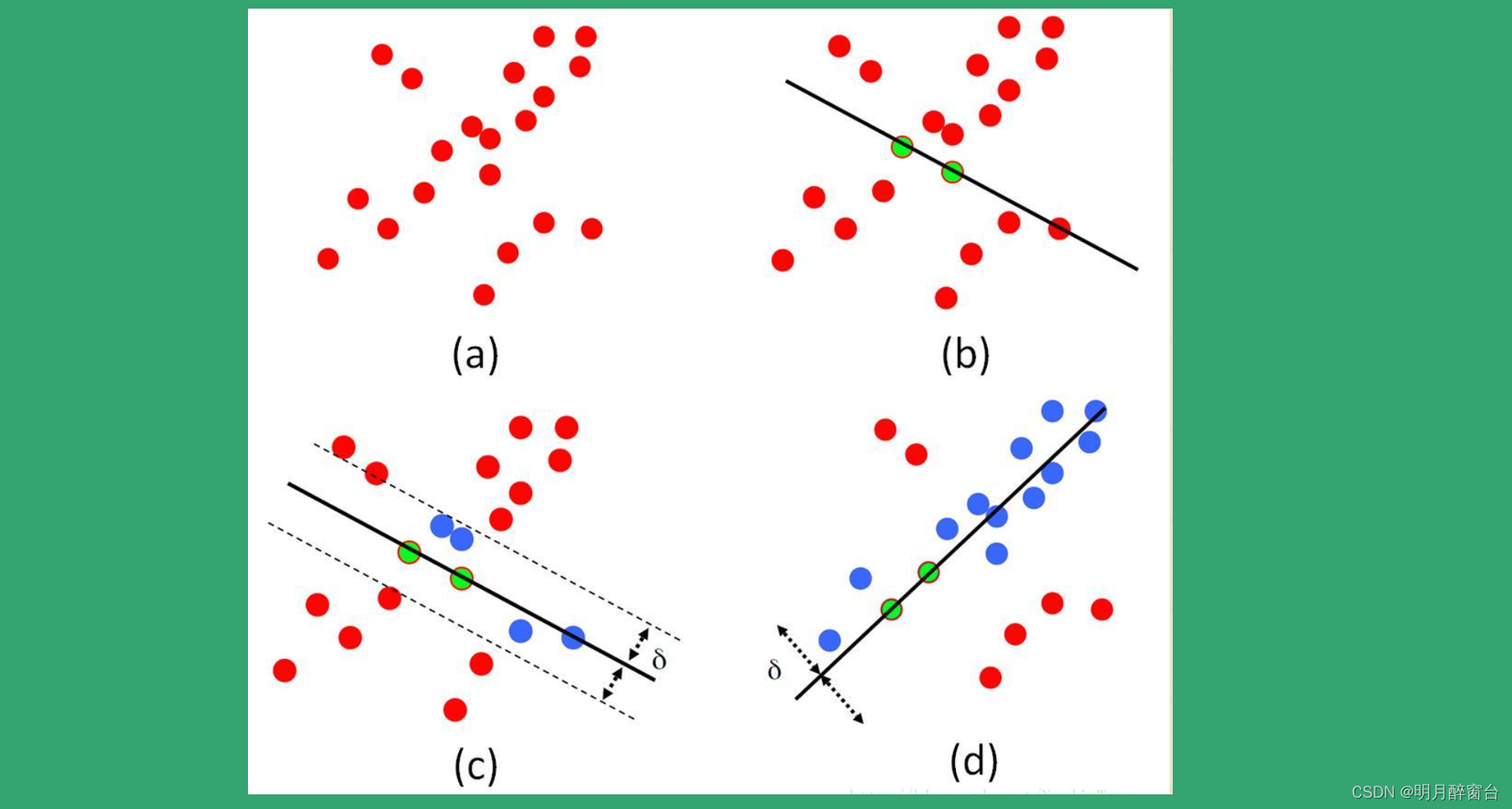
- 其过程如下图所示:
取点集中的两点确定一条直线,然后通过设定规则选取筛选内殿,拿最多的内点拟合出来的模型作为最终的可用模型
1.2 迭代次数推导
- 根据上面RANSAC基本原理的介绍,在这算法流程中存在两个重要的参数需要设置,迭代次数(采样次数)和距离阈值。
迭代的次数我们应该选择多大呢?这个值是否可以事先知道应该设为多少呢?还是只能凭经验决定呢? 这个值其实是可以估算出来的。下面来推算一下。

内点的概率t通常是一个先验值。然后P 是我们希望RANSAC得到正确模型的概率。如果事先不知道t 的值,可以使用自适应迭代次数的方法。也就是一开始设定一个无穷大的迭代次数,然后每次更新模型参数估计的时候,用当前的内点比值当成t 来估算出迭代次数。
1.3 与最小二乘区别
- 最小二乘法尽量去适应包括外点在内的所有点。因此,最小二乘法只适合与误差较小的情况。假使需要从一个噪音较大的数据集中提取模型(比方说只有20%的数据时符合模型的)时,最小二乘法就显得力不从心了。
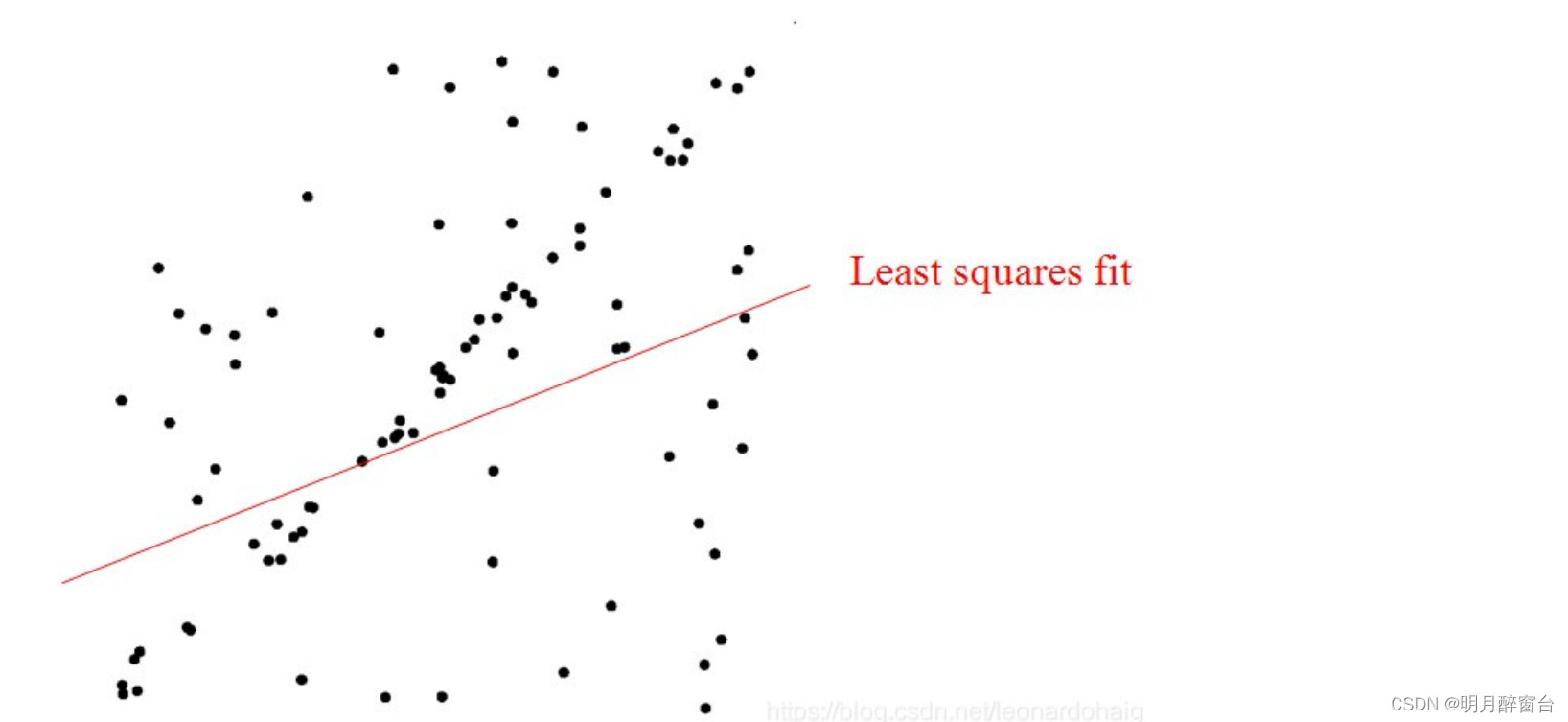
- RANSAC相当于一个概率模型,它通过计算内点出现的概率,找出噪点之外的点集拟合出的 最优模型,通常更能表示系统属性。其相当于迭代使用最小二乘法+抽样测试。
1.4 代码实现
- C++实现:
//====================================================================//
//Program:RANSAC直线拟合,并与最小二乘法结果进行对比
//====================================================================//
#include <iostream>
#include <opencv2/opencv.hpp>
//RANSAC 拟合2D 直线
//输入参数:points--输入点集
// iterations--迭代次数
// sigma--数据和模型之间可接受的差值,车道线像素宽带一般为10左右
// (Parameter use to compute the fitting score)
// k_min/k_max--拟合的直线斜率的取值范围.
// 考虑到左右车道线在图像中的斜率位于一定范围内,
// 添加此参数,同时可以避免检测垂线和水平线
//输出参数:line--拟合的直线参数,It is a vector of 4 floats
// (vx, vy, x0, y0) where (vx, vy) is a normalized
// vector collinear to the line and (x0, y0) is some
// point on the line.
//返回值:无
void fitLineRansac(const std::vector<cv::Point2f>& points,
cv::Vec4f &line,
int iterations = 1000,
double sigma = 1.,
double k_min = -7.,
double k_max = 7.)
{
unsigned int n = points.size();
if(n<2)
{
return;
}
cv::RNG rng;
double bestScore = -1.;
for(int k=0; k<iterations; k++)
{
int i1=0, i2=0;
while(i1==i2)
{
i1 = rng(n);
i2 = rng(n);
}
const cv::Point2f& p1 = points[i1];
const cv::Point2f& p2 = points[i2];
cv::Point2f dp = p2-p1;//直线的方向向量
dp *= 1./norm(dp);
double score = 0;
if(dp.y/dp.x<=k_max && dp.y/dp.x>=k_min )
{
for(int i=0; i<n; i++)
{
cv::Point2f v = points[i]-p1;
double d = v.y*dp.x - v.x*dp.y;//向量a与b叉乘/向量b的摸.||b||=1./norm(dp)
//score += exp(-0.5*d*d/(sigma*sigma));//误差定义方式的一种
if( fabs(d)<sigma )
score += 1;
}
}
if(score > bestScore)
{
line = cv::Vec4f(dp.x, dp.y, p1.x, p1.y);
bestScore = score;
}
}
}
int main()
{
cv::Mat image(720,1280,CV_8UC3,cv::Scalar(125,125,125));
//以车道线参数为(0.7657,-0.6432,534,548)生成一系列点
double k = -0.6432/0.7657;
double b = 548 - k*534;
std::vector<cv::Point2f> points;
for (int i = 360; i < 720; i+=10)
{
cv::Point2f point(int((i-b)/k),i);
points.emplace_back(point);
}
//加入直线的随机噪声
cv::RNG rng((unsigned)time(NULL));
for (int i = 360; i < 720; i+=10)
{
int x = int((i-b)/k);
x = rng.uniform(x-10,x+10);
int y = i;
y = rng.uniform(y-30,y+30);
cv::Point2f point(x,y);
points.emplace_back(point);
}
//加入噪声
for (int i = 0; i < 720; i+=20)
{
int x = rng.uniform(1,640);
int y = rng.uniform(1,360);
cv::Point2f point(x,y);
points.emplace_back(point);
}
int n = points.size();
for (int j = 0; j < n; ++j)
{
cv::circle(image,points[j],5,cv::Scalar(0,0,0),-1);
}
//RANSAC 拟合
if(1)
{
cv::Vec4f lineParam;
fitLineRansac(points,lineParam,1000,10);
double k = lineParam[1] / lineParam[0];
double b = lineParam[3] - k*lineParam[2];
cv::Point p1,p2;
p1.y = 720;
p1.x = ( p1.y - b) / k;
p2.y = 360;
p2.x = (p2.y-b) / k;
cv::line(image,p1,p2,cv::Scalar(0,255,0),2);
}
//最小二乘法拟合
if(1)
{
cv::Vec4f lineParam;
cv::fitLine(points,lineParam,cv::DIST_L2,0,0.01,0.01);
double k = lineParam[1] / lineParam[0];
double b = lineParam[3] - k*lineParam[2];
cv::Point p1,p2;
p1.y = 720;
p1.x = ( p1.y - b) / k;
p2.y = 360;
p2.x = (p2.y-b) / k;
cv::line(image,p1,p2,cv::Scalar(0,0,255),2);
}
cv::imshow("image",image);
cv::waitKey(0);
return 0;
}

- Python 实现:
#!/usr/bin/env python3
#coding=utf-8
#============================#
#Program:RANSAC_Line.py
===========#
import numpy as np
import random
import math
import cv2
def fitLineRansac(points,iterations=1000,sigma=1.0,k_min=-7,k_max=7):
"""
RANSAC 拟合2D 直线
:param points:输入点集,numpy [points_num,1,2],np.float32
:param iterations:迭代次数
:param sigma:数据和模型之间可接受的差值,车道线像素宽带一般为10左右
(Parameter use to compute the fitting score)
:param k_min:
:param k_max:k_min/k_max--拟合的直线斜率的取值范围.
考虑到左右车道线在图像中的斜率位于一定范围内,
添加此参数,同时可以避免检测垂线和水平线
:return:拟合的直线参数,It is a vector of 4 floats
(vx, vy, x0, y0) where (vx, vy) is a normalized
vector collinear to the line and (x0, y0) is some
point on the line.
"""
line = [0,0,0,0]
points_num = points.shape[0]
if points_num<2:
return line
bestScore = -1
for k in range(iterations):
i1,i2 = random.sample(range(points_num), 2)
p1 = points[i1][0]
p2 = points[i2][0]
dp = p1 - p2 #直线的方向向量
dp *= 1./np.linalg.norm(dp) # 除以模长,进行归一化
score = 0
a = dp[1]/dp[0]
if a <= k_max and a>=k_min:
for i in range(points_num):
v = points[i][0] - p1
dis = v[1]*dp[0] - v[0]*dp[1]#向量a与b叉乘/向量b的摸.||b||=1./norm(dp)
# score += math.exp(-0.5*dis*dis/(sigma*sigma))误差定义方式的一种
if math.fabs(dis)<sigma:
score += 1
if score > bestScore:
line = [dp[0],dp[1],p1[0],p1[1]]
bestScore = score
return line
if __name__ == '__main__':
image = np.ones([720,1280,3],dtype=np.ubyte)*125
# 以车道线参数为(0.7657, -0.6432, 534, 548)生成一系列点
k = -0.6432 / 0.7657
b = 548 - k * 534
points = []
for i in range(360,720,10):
point = (int((i-b)/k),i)
points.append(point)
# 加入直线的随机噪声
for i in range(360,720,10):
x = int((i-b)/k)
x = random.sample(range(x-10,x+10),1)
y = i
y = random.sample(range(y - 30, y + 30),1)
point = (x[0],y[0])
points.append(point)
# 加入噪声
for i in range(0,720,20):
x = random.sample(range(1, 640), 1)
y = random.sample(range(1, 360), 1)
point = (x[0], y[0])
points.append(point)
for point in points:
cv2.circle(image,point,5,(0,0,0),-1)
points = np.array(points).astype(np.float32)
points = points[:,np.newaxis,:]
# RANSAC 拟合
if 1:
[vx, vy, x, y] = fitLineRansac(points,1000,10)
k = float(vy) / float(vx) # 直线斜率
b = -k * x + y
p1_y = 720
p1_x = (p1_y-b) / k
p2_y = 360
p2_x = (p2_y-b) / k
p1 = (int(p1_x),int(p1_y))
p2 = (int(p2_x), int(p2_y))
cv2.line(image,p1,p2,(0,255,0),2)
# 最小二乘法拟合
if 1:
[vx, vy, x, y] = cv2.fitLine(points, cv2.DIST_L2, 0, 0.1, 0.01)
k = float(vy) / float(vx) # 直线斜率
b = -k * x + y
p1_y = 720
p1_x = (p1_y - b) / k
p2_y = 360
p2_x = (p2_y - b) / k
p1 = (int(p1_x), int(p1_y))
p2 = (int(p2_x), int(p2_y))
cv2.line(image, p1, p2, (0, 0, 255), 2)
cv2.imshow('image',image)
cv2.waitKey(0)
2. 特征匹配
- 基于特征的图像匹配中会存在误匹配对,因此为提高匹配率,在粗匹配的基础上实现精匹配,可采用下面两种方法:
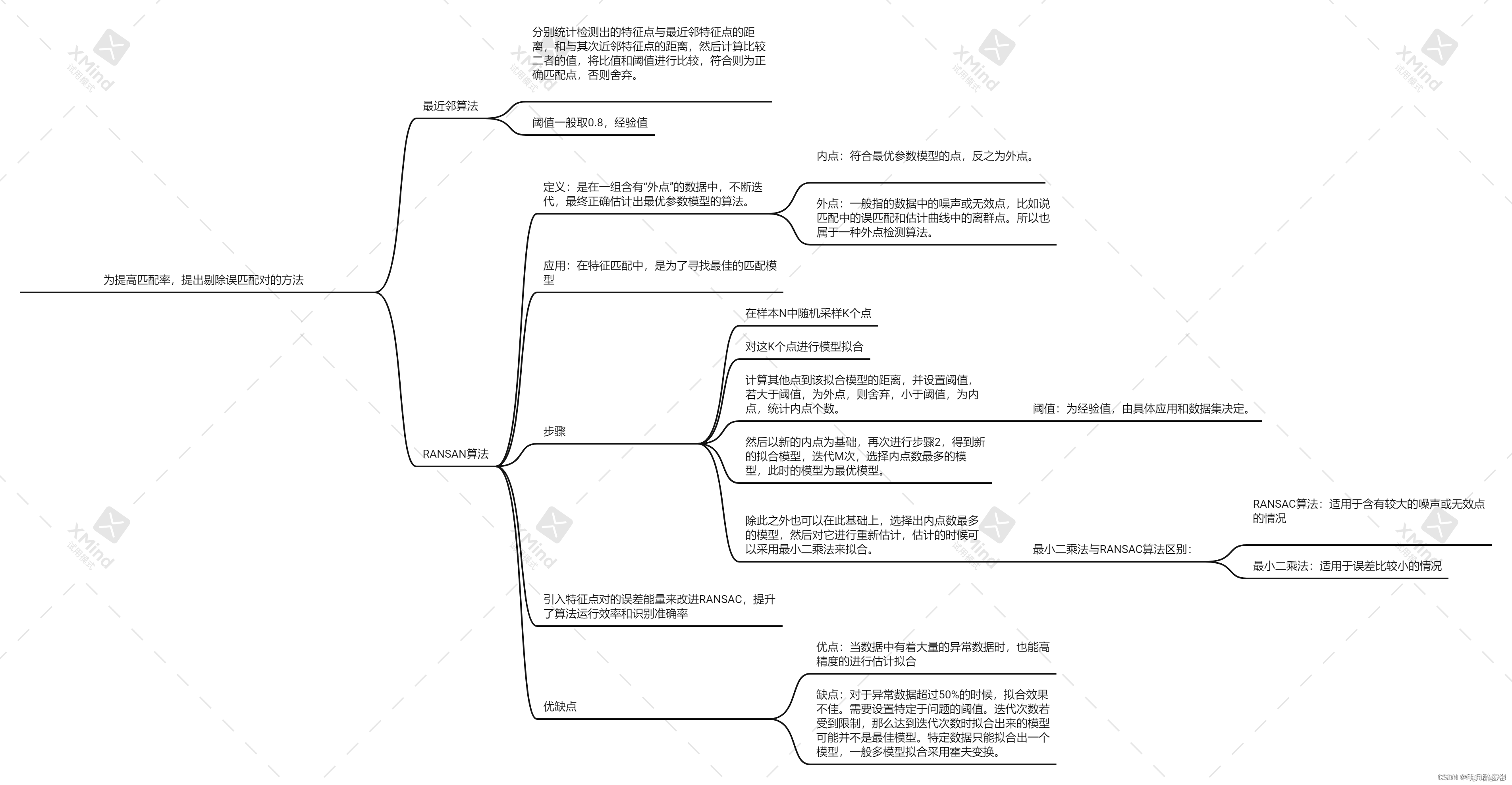
- 用RANSAC算法来寻找最佳单应性矩阵H,在此先提取SIFT特征点进行最近邻粗匹配,然后采取Ransac进行细匹配,最后再进行变换矩阵求解
- 代码实现如下:
//RANSAC算法
int main()
{
Mat img_object = imread("./data/101.png", IMREAD_GRAYSCALE);
Mat img_scene = imread("./data/100.png", IMREAD_GRAYSCALE);
if (img_object.empty() || img_scene.empty())
{
cout << "Could not open or find the image!\n" << endl;
return -1;
}
//-- Step 1: Detect the keypoints using SURF Detector, compute the descriptors
int minHessian = 800; // default: 400
Ptr<SURF> surf = SURF::create(800);
std::vector<KeyPoint> keypoints_object, keypoints_scene;
Mat descriptors_object, descriptors_scene;
surf->detectAndCompute(img_object, noArray(), keypoints_object, descriptors_object);
surf->detectAndCompute(img_scene, noArray(), keypoints_scene, descriptors_scene);
//-- Step 2: Matching descriptor vectors with a FLANN based matcher
// Since SURF is a floating-point descriptor NORM_L2 is used
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create(DescriptorMatcher::FLANNBASED);
std::vector< std::vector<DMatch> > knn_matches;
matcher->knnMatch(descriptors_object, descriptors_scene, knn_matches, 2);
//-- Filter matches using the Lowe's ratio test
const float ratio_thresh = 0.75f;
std::vector<DMatch> good_matches;
for (size_t i = 0; i < knn_matches.size(); i++)
{
if (knn_matches[i][0].distance < ratio_thresh * knn_matches[i][1].distance)
{
good_matches.push_back(knn_matches[i][0]);
}
}
//-- Draw matches
Mat img_matches;
drawMatches(img_object, keypoints_object, img_scene, keypoints_scene, good_matches, img_matches, Scalar::all(-1),
Scalar::all(-1), std::vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);
//-- Localize the object
std::vector<Point2f> obj;
std::vector<Point2f> scene;
for (size_t i = 0; i < good_matches.size(); i++)
{
//-- Get the keypoints from the good matches
obj.push_back(keypoints_object[good_matches[i].queryIdx].pt);
scene.push_back(keypoints_scene[good_matches[i].trainIdx].pt);
}
vector<uchar>inliers;
Mat H = findHomography(obj, scene, inliers, RANSAC);
//-- Draw matches with RANSAC
Mat img_matches_ransac;
std::vector<DMatch> good_matches_ransac;
for (size_t i = 0; i < inliers.size(); i++)
{
if (inliers[i])
{
good_matches_ransac.push_back(good_matches[i]);
}
}
drawMatches(img_object, keypoints_object, img_scene, keypoints_scene, good_matches_ransac, img_matches_ransac, Scalar::all(-1),
Scalar::all(-1), std::vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);
namedWindow("img_matches", WINDOW_NORMAL);
imshow("img_matches", img_matches);
imwrite("img_matches.jpg", img_matches);
namedWindow("img_matches_ransac", WINDOW_NORMAL);
imshow("img_matches_ransac", img_matches_ransac);
imwrite("img_matches_ransac.jpg", img_matches_ransac);
waitKey();
return 0;
}
- 只进行knn匹配与加上Ransac匹配的效果对比图如下:

参考:
1.https://blog.csdn.net/leonardohaig/article/details/104570965?spm=1001.2014.3001.5506
2.https://blog.csdn.net/H19981118/article/details/122014318?spm=1001.2014.3001.5506











![[原创] ElasticSearch集群故障案例分析: 警惕通配符查询](https://img-blog.csdnimg.cn/img_convert/9e5fbae978b8c8e770c7f0712392a1a9.png)