目录

一、关于公约数

二、计算最大公约数的方法 

1. 辗转相除法（欧几里得算法）

2. 更相减损法（辗转相减法）

3. 分解质因数法

4. 穷举法 

5. 递归法

6. 短除法

三、总结

---

一、关于公约数

首先 ，先介绍一下公约数：

公约数（公因数），一个能被若干个整数同时整除的的整数，公约数中最大的称为最大公约数。

公约数与公倍数相反，就是既是A的约数同时也是B的约数的数，12和15的公约数有1，3，最大公约数就是3。再举个例子，30和40，它们的公约数有1，2，5，10，最大公约数是10。

计算两个数组的最大公约数，例如计算 a,b两个数的最大公约数。

二、计算最大公约数的方法 

1. 辗转相除法（欧几里得算法）

第一步，先是两个数进行 模运算,来求余数   即 a%b

①当a可以被b整除时 （a%b == 0），直接返回 b , b就是最大公约数。例a = 4;b = 2;a%b==0,所以b = 2,就是这两个数的最大公约数。

②当a%b != 0时，则进行辗转交换，这里用第三个变量来接收 c = a%b; 用 a 来接收 b的值,用b来接收c(余数的值)。

例 a = 6,b = 12; c = a%b = 6;    a = b = 12;  b = c = 6;  a%b = 12%6 = 0。 最大公因数为 6。

共有约数中最大的一个

③重复上述①和② 

算法流程图

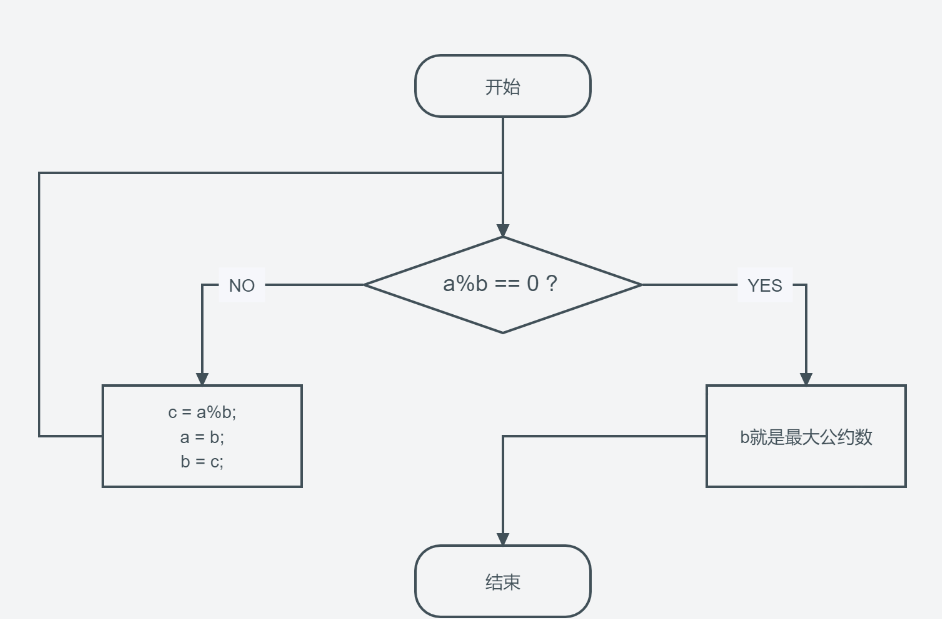
代码展示 

//求最大公约数  辗转相除法
#include <stdio.h>
int fun(int a,int b)
{
	while (a % b != 0)
	{
		int c = a % b;
		a = b;
		b = c;
	}
	return b;
}
int main() 
{
	int a = 0;
	int b = 0;
	scanf("%d %d",&a,&b);
	int ret = fun(a,b);
	printf("最大公约数为：%d",ret);
	return 0;
}

示例：

2. 更相减损法（辗转相减法）

更相减损术是出自《九章算术》的一种求最大公约数的算法，它原本是为约分而设计的，但它适用于任何需要求最大公约数的场合。

思想

原文是

可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之。

翻译：

第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；

若不是则执行第二步。

第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。

则第一步中约掉的若干个2的积与第二步中等数的乘积就是所求的最大公约数。

其中所说的“等数”，就是公约数。求“等数”的办法是“更相减损”法。

提取上述的一些思想

例 a = 12, b = 18;  b = b - a = 18 - 12 = 6; a >b; a = a - b = 12 - 6 = 6; a = b = 6; 。

算法流程图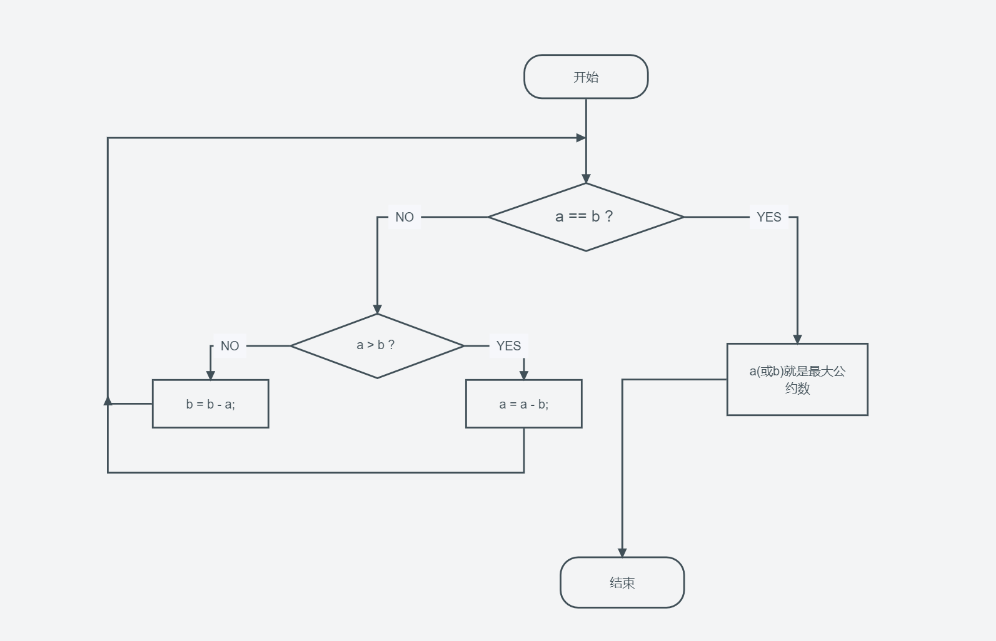

代码展示 

//更相减损法（辗转相减法）
#include<stdio.h>
int main() 
{
	int a = 0;
	int b = 0;
	scanf("%d %d",&a,&b);
	while (a != b) 
	{
		if (a > b)
			a = a - b;
		else
			b = b - a;
	}
	printf("最大公约数是：%d",a);
	return 0;
}

示例

3. 分解质因数法

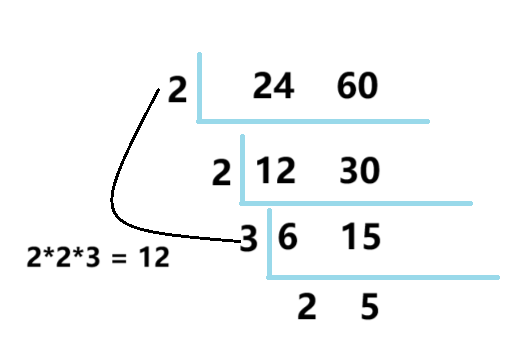
 把每个数分别分解质因数，再把各数中的全部公有质因数提取出来连乘，所得的积就是这几个数的最大公约数

例如：求24和60的最大公约数，先分解质因数，得24=2×2×2×3，60=2×2×3×5，24与60的全部公有的质因数是2、2、3，它们的积是2×2×3=12，所以，（24，60）= 12

代码展示

#include<stdio.h>
void fun(int * arr,int n)
{
	int i = 2, j = 0;
	while (n > 1)
	{
		if (n % i == 0)
		{
			arr[j++] = i;
			n /= i;
		}
		else 
		{
			i++;
		}
	}
}
int gcd(int a,int b) 
{
	//因为要进行找这个数的共有的因数，所以这里用数组来接收
	int arr_a[100] = {0};//放a的所有因数
	int arr_b[100] = {0};//放b的所有因数
	//进行放因数
	fun(arr_a,a);
	fun(arr_b,b);

	//找出公共的因数，然后相乘
	int i = 0, j = 0, ret = 1;
	while (arr_a[i] != 0 && arr_b[j] != 0) 
	{
		if (arr_a[i] == arr_b[j]) 
		{
			ret *= arr_a[i];
			i++;
			j++;
		}
		else if (arr_a[i] > arr_b[j])
		{
			j++;
		}
		else
		{
			i++;
		}
	}
	return ret;
}
int main() 
{
	int a = 0;
	int b = 0;
	scanf("%d %d",&a,&b);
	int ret = gcd(a,b);//最大公因数
	printf("%d和%d的最大公因数是：%d",a,b,ret);
	return 0;
}

 

4. 穷举法 

 穷举法的基本思想是根据题目的部分条件确定答案的大致范围，并在此范围内对所有可能的情况逐一验证，直到全部情况验证完毕。若某个情况验证符合题目的全部条件，则为本问题的一个解；若全部情况验证后都不符合题目的全部条件，则本题无解。穷举法也称为枚举法

这里的枚举法就是 先 用一个临时变量来接收（a或b） 其中的一个数，然后连个数进行模运算，两个数都模这个临时变量等于零就是最大公约数，否则临时变量每次减一,然后重复上述。

代码展示 

//穷举法
#include<stdio.h>
int main() 
{
	int a = 0;
	int b = 0;
	scanf("%d %d",&a,&b);
	int t = a;
	while (t--)
	{
		if (a % t == 0 && b % t == 0)
			break;
	}
	printf("%d",t);
	return 0;
}

5. 递归法

这里的递归法是基于辗转相除法的思想，然后通过递归来实现。

两个数的最大公约数 ，其中 较小的数  和 两个数相除的余数 的最大公约数

当 y / x%y == 0 时 ， y就是最大公约数。

不为0， 就递归 gcd(y,x%y),  gcd 下方代码有描述

算法流程图

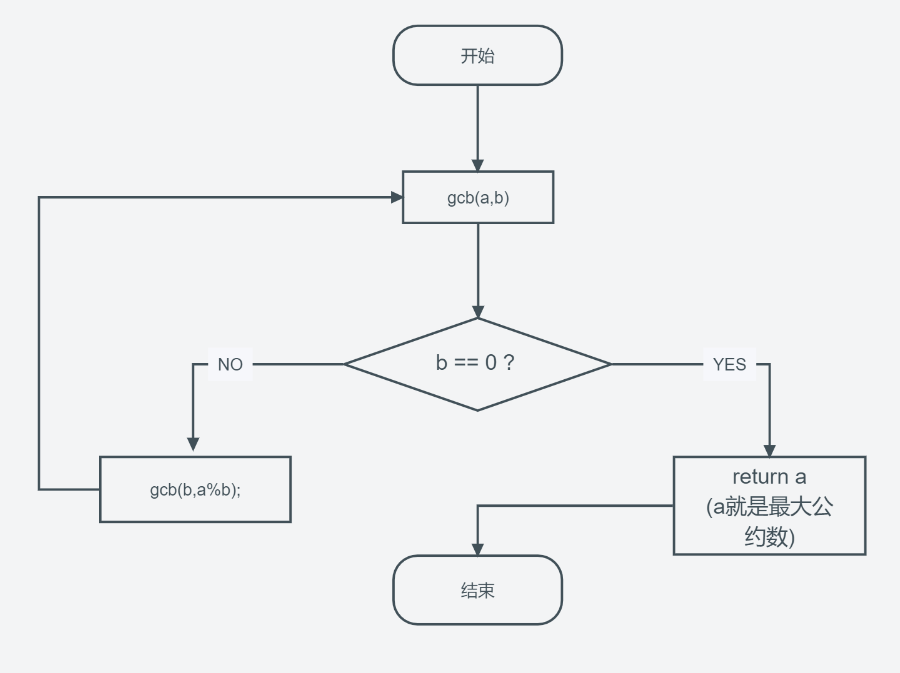
代码实现 

#include<stdio.h>
int gcd(int a, int b)
{
	if (b == 0)
		return a;
	else
		return gcd(b,a%b);
}
int main()
{
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	int ret = gcd(a,b);
	printf("%d",ret);
	return 0;
}

6. 短除法

例如：求12与18的最大公因数。以下如有约数出现则为因数

短除法例题：

12的因数有：1、2、3、4、6、12。

18的因数有：1、2、3、6、9、18。

12与18的公因数有：1、2、3、6。

12与18的最大公因数是6。

算法思想：

第一步：先是分别计算处两个数的所有因数，然后分别用数组来进行存放两个数组的所有因数（这里也可以只用一个数组）本例中为方便大家的理解采用两个数组进行存放。

注意：这里的存放也是有技巧的，这里采取的是从大到小进行排序的（当然也可以进行采取从小到大进行排序）

第二步：进行遍历找出相同的因数进行比较，使用一个临时变量用来存放最大公因数

 代码展示

#include<stdio.h>
void fac(int* arr, int n)
{
	int i = 0;
	int j = 0;
	int k = 0;
	for (i = 1; i <= n; i++)
	{
		if (n % i == 0)
		{
			arr[k++] = i;
		}
	}
}
int gcd(int a, int b)
{
	int arr1[100] = { 0 };
	int arr2[100] = { 0 };
	fac(arr1, a);
	fac(arr2, b);

	//求同找最大
	int i = 0, j = 0, max = 1;
	while (arr1[i] != 0 && arr2[j] != 0)
	{
		if (arr1[i] == arr2[j])
		{
			if (max < arr1[i])
			{
				max = arr1[i];
			}
			i++;
			j++;
		}
		else if (arr1[i] < arr2[j])
		{
			i++;
		}
		else
		{
			j++;
		}
	}
	return max;
}
int main()
{
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	int ret = gcd(a, b);
	printf("%d 和 %d 的最大公因数为 %d",a,b ,ret);
	return 0;
}

三、总结

这里比较推荐是用 辗转相除法（欧几里得算法）和 《九章算术》中的 更相减损法

多说一下，因为当时阿明浅浅学过遍辗转相除法，然后不久后就忘干净了，用的时候还要再去反复找，为了方便使用，干脆把 求解最大公约数 的几种常见的方法详细介绍一下，虽然不是最好，但是多少希望对大家有些帮助！

希望大家对这些方法，有更加深刻的印象。

加油！！！