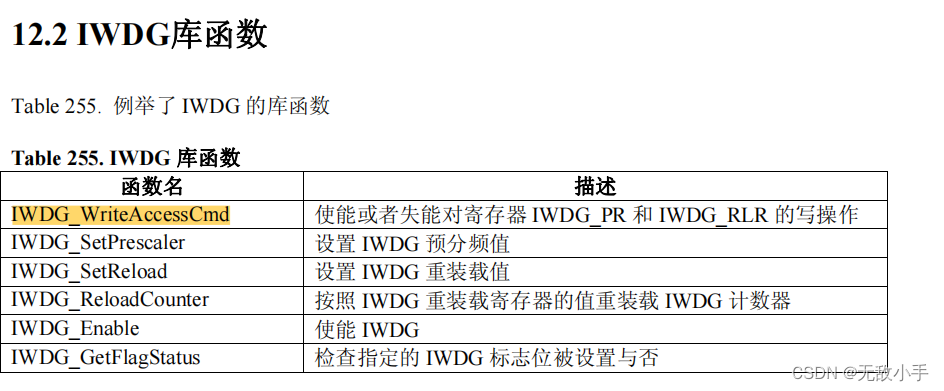
回归分析是统计学中的一个重要分支，它用于建立一个或多个自变量和一个因变量之间的关联模型。在本博客中，我们将深入探讨线性回归和逻辑回归这两种常见的回归分析方法，并通过Python示例进行分析。

---

1.线性回归

1.1 模型介绍

  线性回归是回归分析中的基本方法之一，它用于建立自变量和因变量之间的线性关系模型。在线性回归中，我们假设因变量是自变量的线性组合，即：
$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\dots +{\beta }_n{X}_n+ϵ$$
其中，$Y$ 是因变量，$X_1,X_2,\dots ,X_n$ 是自变量，${\beta }_0,{\beta }_1,{\beta }_2,\dots ,{\beta }_n$ 是回归系数，$ϵ$ 是误差项。

1.2 示例分析

现在，让我们使用Python来进行一个简单的线性回归示例：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 创建一些示例数据
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 * X + 1 + 0.1 * np.random.randn(100, 1)

# 创建线性回归模型
model = LinearRegression()

# 拟合模型
model.fit(X, y)

# 打印回归系数
print("回归系数 (斜率):", model.coef_)
print("截距:", model.intercept_)

# 绘制数据和拟合线
plt.scatter(X, y)
plt.plot(X, model.predict(X), color='red', linewidth=3)
plt.xlabel("自变量")
plt.ylabel("因变量")
plt.title("线性回归示例")
plt.show()

结果：
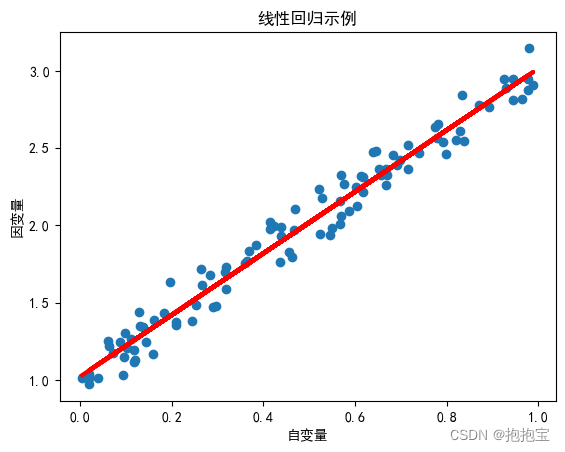该回归方程的回归系数和截距如下：
  回归系数 (斜率): [[1.9936935]]
  截距: [1.02221511]

2.逻辑回归

2.1 模型原理

  逻辑回归是一种用于解决分类问题的回归分析方法，它预测一个二进制输出（0或1）。逻辑回归基于逻辑函数（也称为S形函数），它将线性组合的结果映射到一个介于0和1之间的概率值。
逻辑回归的模型表达式如下：
$$P(Y=1)=\frac{1}{1+e^{-({\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\dots +{\beta }_n{X}_n)}}$$
其中，$P(Y=1)$ 是因变量为1的概率，$X_1,X_2,\dots ,X_n$ 是自变量，${\beta }_0,{\beta }_1,{\beta }_2,\dots ,{\beta }_n$ 是回归系数。

2.2 示例分析

下面是一个使用Python进行逻辑回归的示例：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

# 创建一个示例数据集
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建逻辑回归模型
model = LogisticRegression()

# 拟合模型
model.fit(X_train, y_train)

# 预测测试集
y_pred = model.predict(X_test)

# 绘制决策边界
xx, yy = np.meshgrid(np.linspace(X[:, 0].min() - 1, X[:, 0].max() + 1, 100),
                     np.linspace(X[:, 1].min() - 1, X[:, 1].max() + 1, 100))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=plt.cm.coolwarm)
plt.xlabel("自变量1")
plt.ylabel("自变量2")
plt.title("逻辑回归示例")
plt.show()

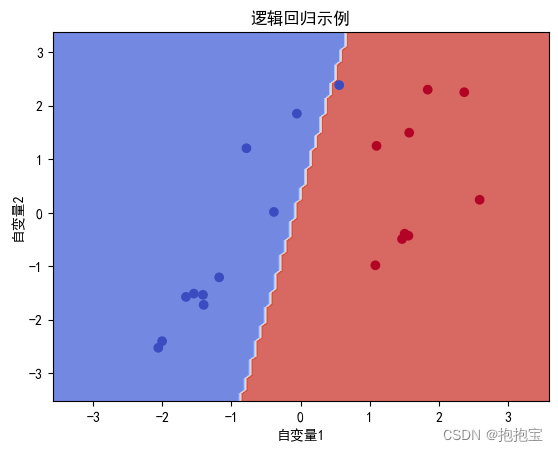
结果图：
  回归分析是数据科学和机器学习中的核心技术之一，线性回归和逻辑回归是两个常用的工具，用于建立和解释数据之间的关系。通过Python示例，我们可以更好地理解和应用这些方法，以解决实际问题。

---