文章目录
- 分类模型的评估
- 混淆矩阵
- 精确率和召回率
- 接口介绍
- 其他的补充
- 朴素贝叶斯
- 基础原理介绍
- 拉普拉斯平滑
- 下面给出应用的例子
- 朴素贝叶斯的思辨
- 决策树
- 基础使用
- 基本原理
- 信息熵
- 信息增益
- 信息增益率
- Gini指数
- 剪枝
- api介绍
- 随机森林------集成学习初识
- 基本使用
- api介绍
分类模型的评估
一般最常见使用的是准确率,即预测结果正确的百分比,我们之前写的那个KNN所使用的就是准确率,但是实际上在很多的别的使用场景上,我们关注的并不只有准确性,比如后面会举一个个人理解的例子,进行分析。
混淆矩阵
在分类任务下,预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合,构成混淆矩阵。
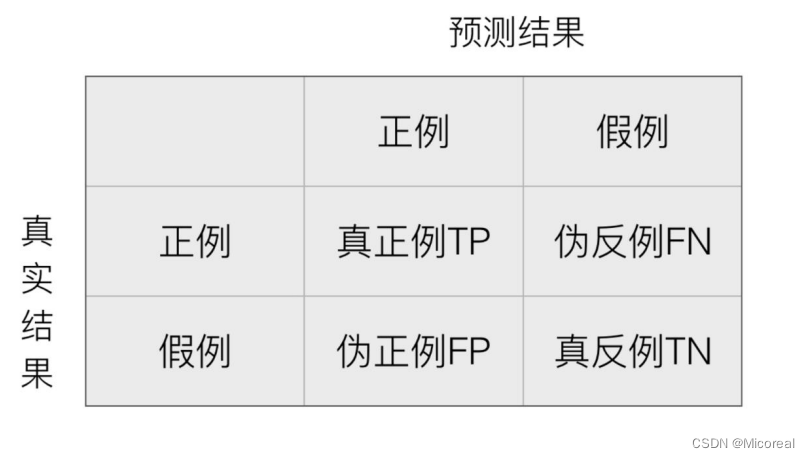
这边的理解我们带入例子,进行理解,并理解一下为什么只有准确度并不能完全说明这个模型预测的好坏,我们把这个带入医生系统,去判断病人是否有病
TP:病人有病,被你预测成有病。
TN:病人没病,被你预测成没病。
FP:病人没病,被你预测成有病。
FN:病人有病,被你预测成没病。
明显对于医生预测系统来说,我们除了关注准确度来说,FN也是一个关键值,对于一个病人有病,却被诊断为没病,这是非常致命的缺陷,我们甚至希望牺牲掉部分准确性,去提升这一事故的发生。
精确率和召回率
精确率:预测结果为正例样本中真实为正例的比例(查得准):TP/TP+FP
召回率:真实为正例的样本中预测结果为正例的比例(查的全,对正样本的区分能力):TP/TP+FN
接口介绍
这个只是做接口介绍,具体的使用放在下面的朴素贝叶斯进行使用。
sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )
y_true:真实目标值
y_pred:估计器预测目标值
labels:指定类别对应的数字
target_names:目标类别名称
return:每个类别精确率与召回率
其他的补充
参考链接:链接1
链接2
朴素贝叶斯
基础原理介绍
在学习概率论的时候,我们已经学习过了朴素贝叶斯,这是一个后验概率。
详细见链接
下面讲点,自己的理解:
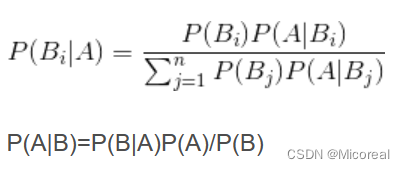
即我们对于这个公式的分类理解:
我们现在想要做一个根据文章出现的关键词,进行判断这篇文章是不是属于科技类的新闻,那么概率就是P(科技|‘云计算’ ‘高帧’ ‘计算机’···),但这个概率明显是没有办法进行求取的,但是我们可以根据这个贝叶斯公式进行转化
直接变成(P(云计算|科技) * P(科技) * ···)/ P(‘云计算’ ‘高帧’ ‘计算机’···)
这明显都可以根据已有的条件进行推出,这也就是这个公式的意义。
朴素贝叶斯的实现API:
sklearn.naive_bayes.MultinomialNB
拉普拉斯平滑
在求取概率的时候,有时候由于每个参数出现的次数太少,然后根据我们上面的公式一个为0之后,那么之后所有的样本都不用进行计算,直接全为0了,所以我们这边采用拉普拉斯平滑进行处理,让其脱离0的局限。
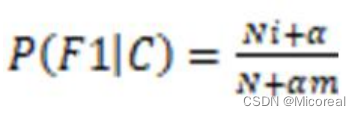
处理就是在求条件概率的时候,上方加上一个alpha,下方加上alpha*样本数目。
实现接口:
sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
下面给出应用的例子
数据就是20类新闻的那个数据。
# 朴素贝叶斯进行文本分类 以及使用检测那个混淆矩阵的 精确率和回归率
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report,roc_auc_score
# 数据准备 sklearn就是好啊,直接给的都不需要进行数据处理
news = fetch_20newsgroups(subset='all', data_home='dataset')
print(len(news.data)) # 看一下共有多少条新闻
# 进行数据分割
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25, random_state=1)
# 开始特征工程的工作 对数据集进行特征抽取 这一部分之前也讲解过,不细看,由于这个数据是纯英文的,所以不需要进行jieba分词
tfidef = TfidfVectorizer()
x_train = tfidef.fit_transform(x_train)
x_test = tfidef.transform(x_test)
# 训练 准备开始训练
# 进行朴素贝叶斯算法的预测,alpha是拉普拉斯平滑系数,分子和分母加上一个系数,分母加alpha*特征词数目
mlt = MultinomialNB(alpha=1.0)
# 开始训练
mlt.fit(x_train, y_train)
# 训练结束 开始预测
y_predict = mlt.predict(x_test)
# 得出准确率,这个是很难提高准确率,为什么呢?
print("准确率为:", mlt.score(x_test, y_test))
# 计算精准率和召回率
print("每个类别的精确率和召回率:\n", classification_report(y_test, y_predict, target_names=news.target_names))
# 把0-19总计20个分类,变为0和1 这个是计算AUC用的,AUC只能用于二分类
y_test = np.where(y_test == 0, 1, 0)
y_predict = np.where(y_predict == 0, 1, 0)
# roc_auc_score的y_test只能是二分类,针对多分类如何计算AUC
print("AUC指标:\n", roc_auc_score(y_test, y_predict))
输出:
18846
准确率为: 0.8518675721561969
每个类别的精确率和召回率:
precision recall f1-score support
alt.atheism 0.91 0.77 0.83 199
comp.graphics 0.83 0.79 0.81 242
comp.os.ms-windows.misc 0.89 0.83 0.86 263
comp.sys.ibm.pc.hardware 0.80 0.83 0.81 262
comp.sys.mac.hardware 0.90 0.88 0.89 234
comp.windows.x 0.92 0.85 0.88 230
misc.forsale 0.96 0.67 0.79 257
rec.autos 0.90 0.87 0.88 265
rec.motorcycles 0.90 0.95 0.92 251
rec.sport.baseball 0.89 0.96 0.93 226
rec.sport.hockey 0.95 0.98 0.96 262
sci.crypt 0.76 0.97 0.85 257
sci.electronics 0.84 0.80 0.82 229
sci.med 0.97 0.86 0.91 249
sci.space 0.92 0.96 0.94 256
soc.religion.christian 0.55 0.98 0.70 243
talk.politics.guns 0.76 0.96 0.85 234
talk.politics.mideast 0.93 0.99 0.96 224
talk.politics.misc 0.98 0.56 0.72 197
talk.religion.misc 0.97 0.26 0.41 132
accuracy 0.85 4712
macro avg 0.88 0.84 0.84 4712
weighted avg 0.87 0.85 0.85 4712
AUC指标:
0.8827602448315142
朴素贝叶斯的思辨
优点:
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
- 分类准确度高,速度快
缺点:
- 需要知道先验概率 P(F1,F2,…|C),因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
- 假设了文章当中一些词语另外一些是独立没关系—-如果有关系,会造成不太靠谱
- 训练集当中去进行统计词这些工作 文章收集的不好,比如有作弊文章,充斥某个词会对结果造成干扰
朴素贝叶斯常用于文本领域,但是现在神经网络的transformer做的更好,朴素贝叶斯也属于lazy learning的类型的。
决策树
基础使用
# 决策树
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier
# 获取数据 观察数据的内容
titan = pd.read_csv("./dataset/titanic/titan_train.csv")
# 确定特征值 目标值
x = titan[["Pclass", "Age", "Sex"]]
y = titan["Survived"]
print(x.info()) # 打印出来说明存在nan
print(x.shape)
print('-'*20)
# 处理空值 直接平均值填写吧
im = SimpleImputer(missing_values=np.nan, strategy='mean')
x['Age'] = im.fit_transform(x[['Age']])
# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
# 查看数据,存在字符串,所以需要转化为one-hot Dict顾名思义需要传入的是字典
transfer = DictVectorizer()
x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.fit_transform(x_test.to_dict(orient="records"))
# 决策树训练
estimator = DecisionTreeClassifier(criterion="entropy", max_depth=5)
estimator.fit(x_train, y_train)
# 模型评估
print(estimator.score(x_test, y_test))
输出:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 3 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Pclass 891 non-null int64
1 Age 714 non-null float64
2 Sex 891 non-null object
dtypes: float64(1), int64(1), object(1)
memory usage: 21.0+ KB
None
(891, 3)
--------------------
0.7757847533632287
基本原理
决策树的基本原理:
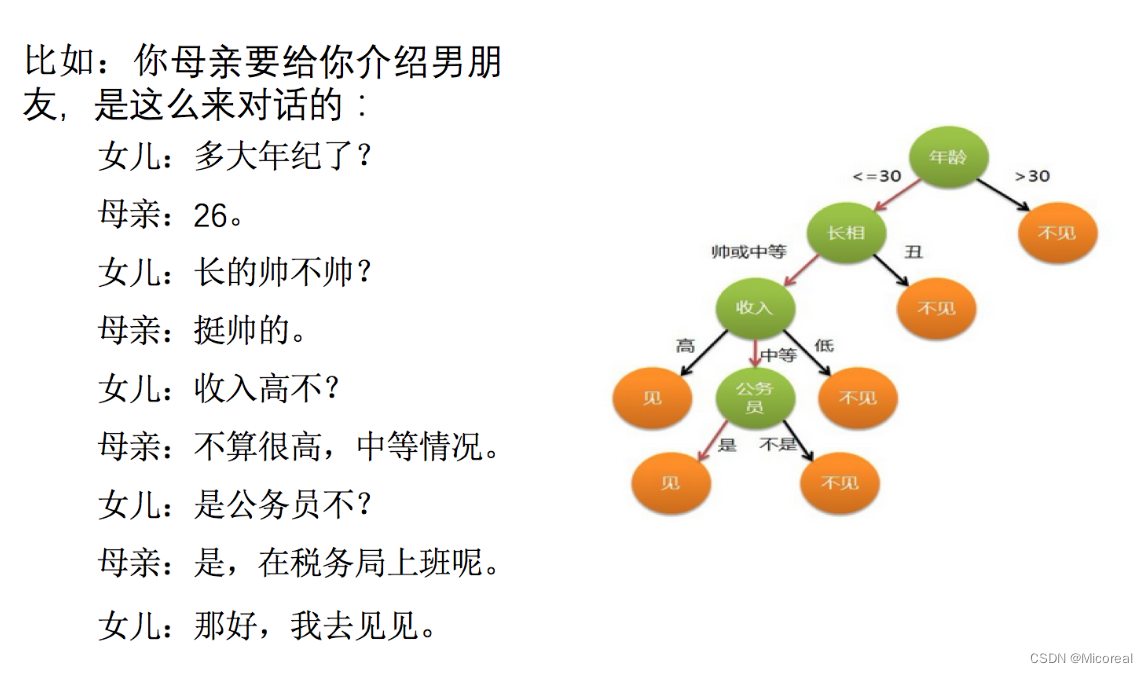
决策树的基本原理就是类似我们的if-else,从根节点开始,不断进行判断,最后走到一个叶子节点,就是我们相对应的结局,而我们需要根据自己的需要去构建出这么一棵决策树,构建决策树要根据什么原则来构建呢?实际上采用的熵
信息熵
系统越有序,熵值越低;系统越混乱或者分散,熵值越高,在之前的决策树,我们采用的是香农的信息熵公式进行判断到底是什么需要优先排在上面,什么排在下面再进行判断。
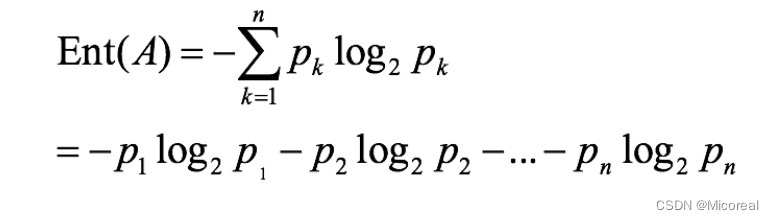
而我么进行排列的顺序一大顺序就是按照信息熵的信息增益来进行判断的。
信息增益
信息增益:以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
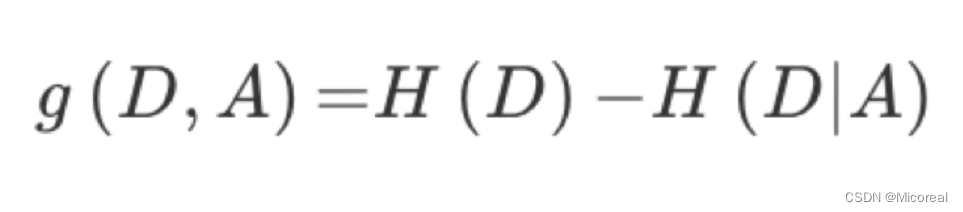
信息增益 = entroy(前) - entroy(后),然后来判断到底是哪一个来的效果更好,就是选择哪一个。
这个就是经典的id3 算法,但是对于id3算法来说,他的一个巨大的缺陷就是他受特征量多的那一个影响太严重,这个需要根据个人的想法进行判断是否采用这个算法。
信息增益率
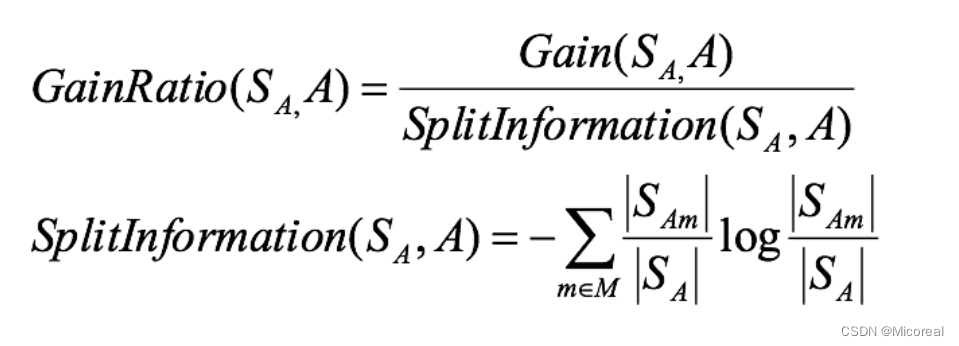
这个就是在原本的计算的时候除掉一个总数。
Gini指数
基尼值Gini(D):从数据集D中随机抽取两个样本,其类别标记不一致的概率。故,Gini(D)值越小,数据集D的纯度越高。
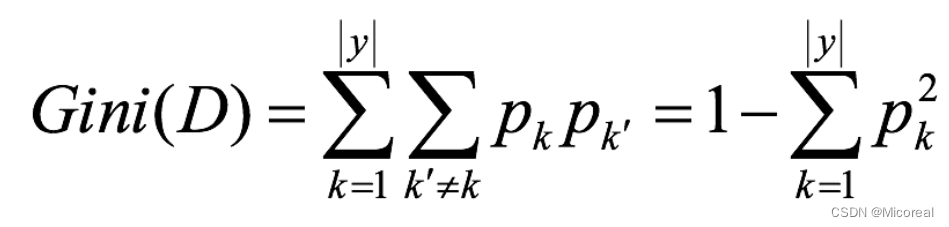
一般,选择使划分后基尼系数最小的属性作为最优化分属性
剪枝
为了防止过拟合现象,需要剪枝进行剪掉我们的部分数据。
预剪枝:
- 每一个结点所包含的最小样本数目,例如10,则该结点总样本数小于10时,则不再分
- 指定树的高度或者深度,例如树的最大深度为4
- 指定结点的熵小于某个值,不再划分。随着树的增长, 在训练样集上的精度是单调上升的, 然而在独立的测试样例上测出的精度先上升后下降。
后剪枝:
实际上就是在看到了前面的效果之后的剪枝,剪枝也跟上面是一致的。
api介绍
class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
criterion 特征选择标准
"gini"或者"entropy",前者代表基尼系数,后者代表信息增益。一默认"gini",即CART算法。
min_samples_split
内部节点再划分所需最小样本数
这个值限制了子树继续划分的条件,如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分。 默认是2.如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。我之前的一个项目例子,有大概10万样本,建立决策树时,我选择了min_samples_split=10。可以作为参考。
min_samples_leaf
叶子节点最少样本数
这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数,或者最少样本数占样本总数的百分比。如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。之前的10万样本项目使用min_samples_leaf的值为5,仅供参考。
max_depth
决策树最大深度
决策树的最大深度,默认可以不输入,如果不输入的话,决策树在建立子树的时候不会限制子树的深度。一般来说,数据少或者特征少的时候可以不管这个值。如果模型样本量多,特征也多的情况下,推荐限制这个最大深度,具体的取值取决于数据的分布。常用的可以取值10-100之间
random_state
随机数种子
随机森林------集成学习初识
基本使用
# 随机森林 使用了集成学习
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
# 还是使用上面的数据 不详细介绍
#----------------------------------------------------------------------
titan = pd.read_csv("./dataset/titanic/titan_train.csv")
x = titan[["Pclass", "Age", "Sex"]]
y = titan["Survived"]
im = SimpleImputer(missing_values=np.nan, strategy='mean')
x['Age'] = im.fit_transform(x[['Age']])
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
transfer = DictVectorizer()
x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.fit_transform(x_test.to_dict(orient="records"))
#----------------------------------------------------------------------
# 随机森林进行训练 随机森林搭配网格训练
rf = RandomForestClassifier()
# n_estimators 代表的就是有几棵树
param = {"n_estimators": [120,200,300], "max_depth": [5, 8, 15, 25, 30]}
gc = GridSearchCV(rf, param_grid=param, cv=2)
gc.fit(x_train, y_train)
print("随机森林预测的准确率为:", gc.score(x_test, y_test))
输出:
随机森林预测的准确率为: 0.7802690582959642
api介绍
sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
n_estimators:integer,optional(default = 10)森林里的树木数量120,200,300,500,800,1200
Criterion:string,可选(default =“gini”)分割特征的测量方法
max_depth:integer或None,可选(默认=无)树的最大深度 5,8,15,25,30
max_features="auto”,每个决策树的最大特征数量
If "auto", then max_features=sqrt(n_features).
If "sqrt", then max_features=sqrt(n_features)(same as "auto").
If "log2", then max_features=log2(n_features).
If None, then max_features=n_features.
bootstrap:boolean,optional(default = True)是否在构建树时使用放回抽样
min_samples_split:节点划分最少样本数
min_samples_leaf:叶子节点的最小样本数
超参数:n_estimator, max_depth, min_samples_split,min_samples_leaf