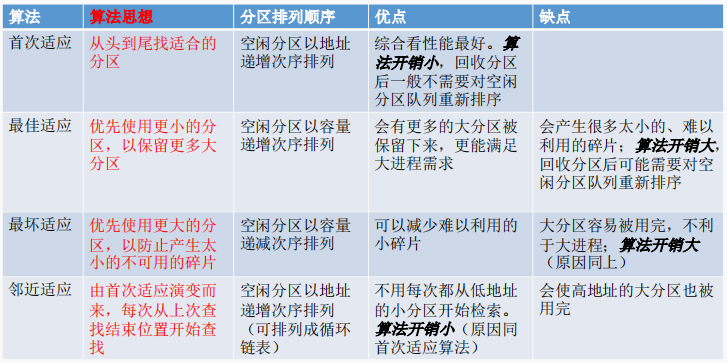
1.特点
https://blog.csdn.net/weixin_57128596/article/details/127030901?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522167176442416800188598723%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=167176442416800188598723&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2blogfirst_rank_ecpm_v1~rank_v31_ecpm-2-127030901-null-null.blog_rank_default&utm_term=B%2B&spm=1018.2226.3001.4450
1.整体有序
2.一个节点下面多个元素
3.非叶子节点没有指向当前数据的指针,叶子节点有
4.节点下的元素是有序的
5.叶子节点包含上面的所有数据,叶子节点之间是一个链表,不需要返回根节点再搜索其他节点**(核心 )**
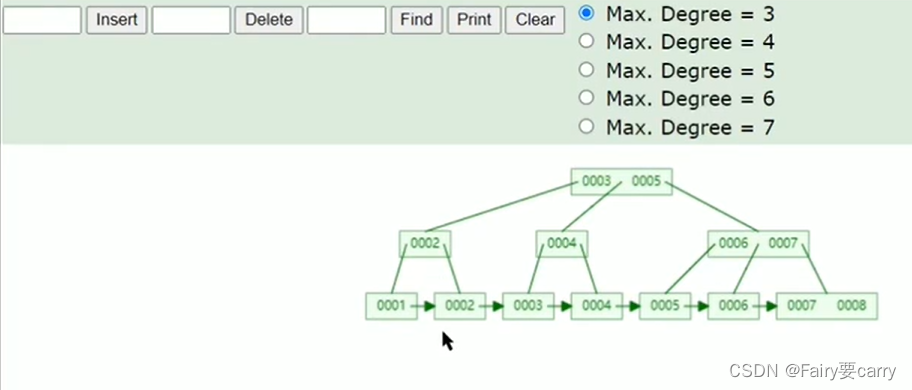
2. 抛出问题:为什么数据库插入数据会默认给你排好序
下图所示:插入了几条数据进入mysql,会根据主键进行排序,用主键效率会高一点,不然一下中间一下下面的,效率肯定受影响,自增往后面叠就行了
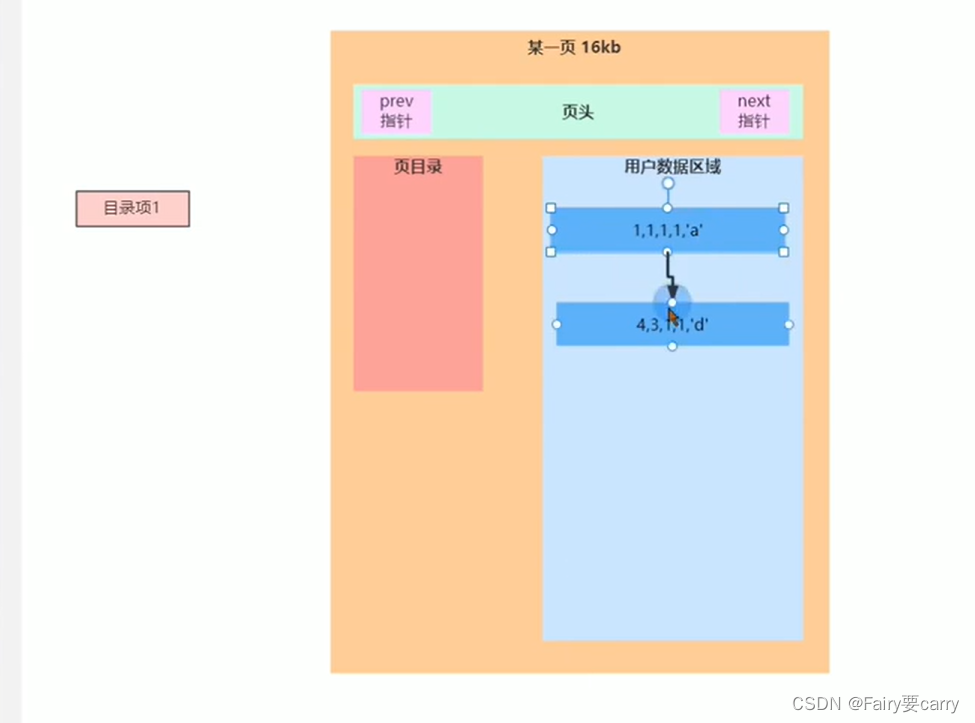
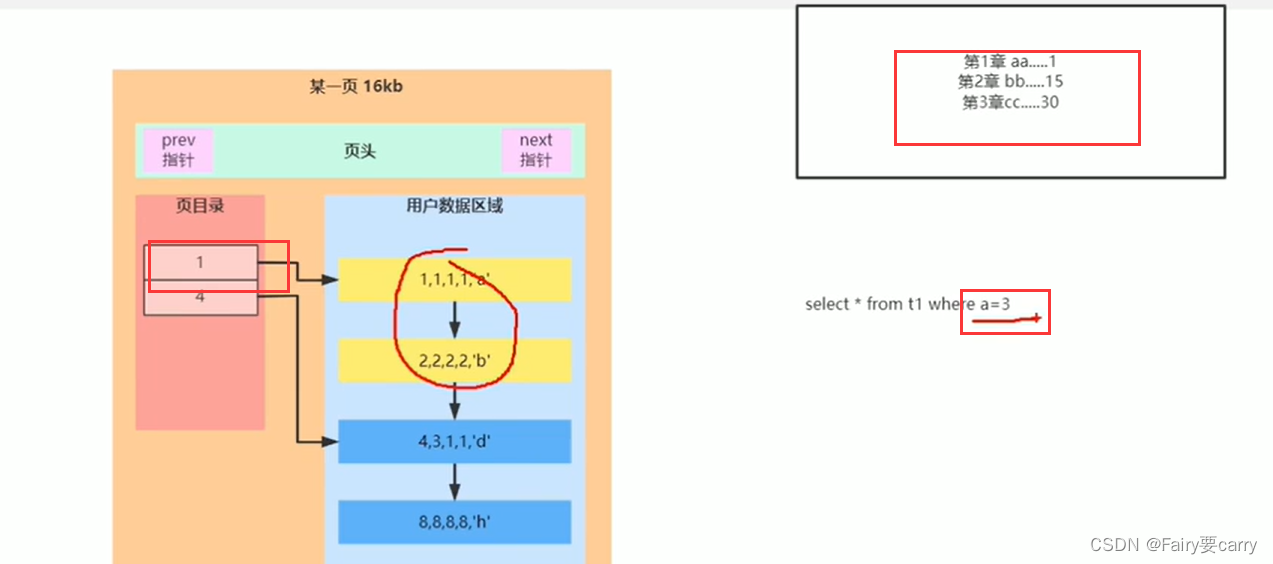
查询
在查询的时候,原先查询数据就像翻书一样一页一页翻,而我们这里你找到了就不会继续向下遍历了
更重要的是设置了目录:
会根据我们设置的主键确定目录,我们只需要判断有没有这个目录就能确定这个数据在不在这里面了,效率非常高,比如查询a=3,目录由主键确定1和4,那么a=3就会从主键为1的地方目录进行遍历寻找,如果遍历完没有就没有**(剩下了很多的遍历)**
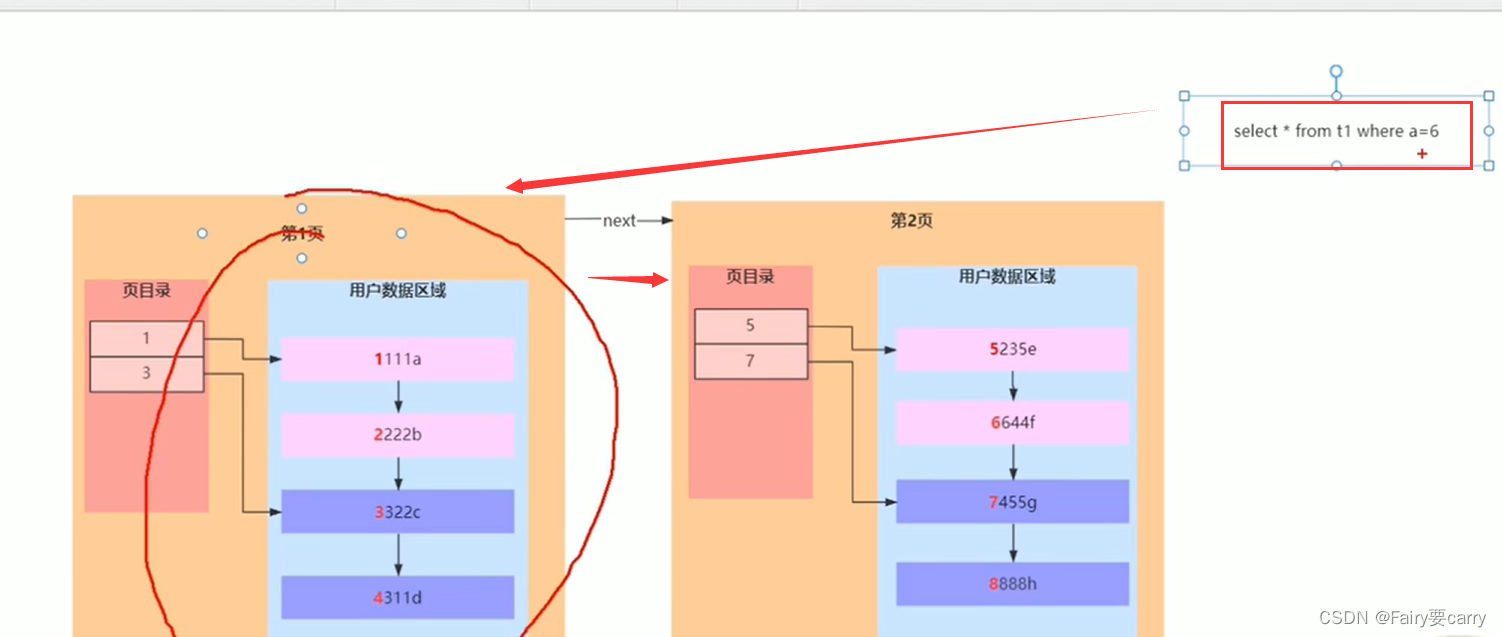
一页只要16kb满了怎么办
如果一页存储插入的数据有限,那么更多的数据就会到第二页上面
当我们进行搜寻的时候就会先遍历第一页,如果第一页没有再在第二页中搜寻——>(页数很多的情况搜索很难,比如数据在100页但是我还遍历了前99页的目录)
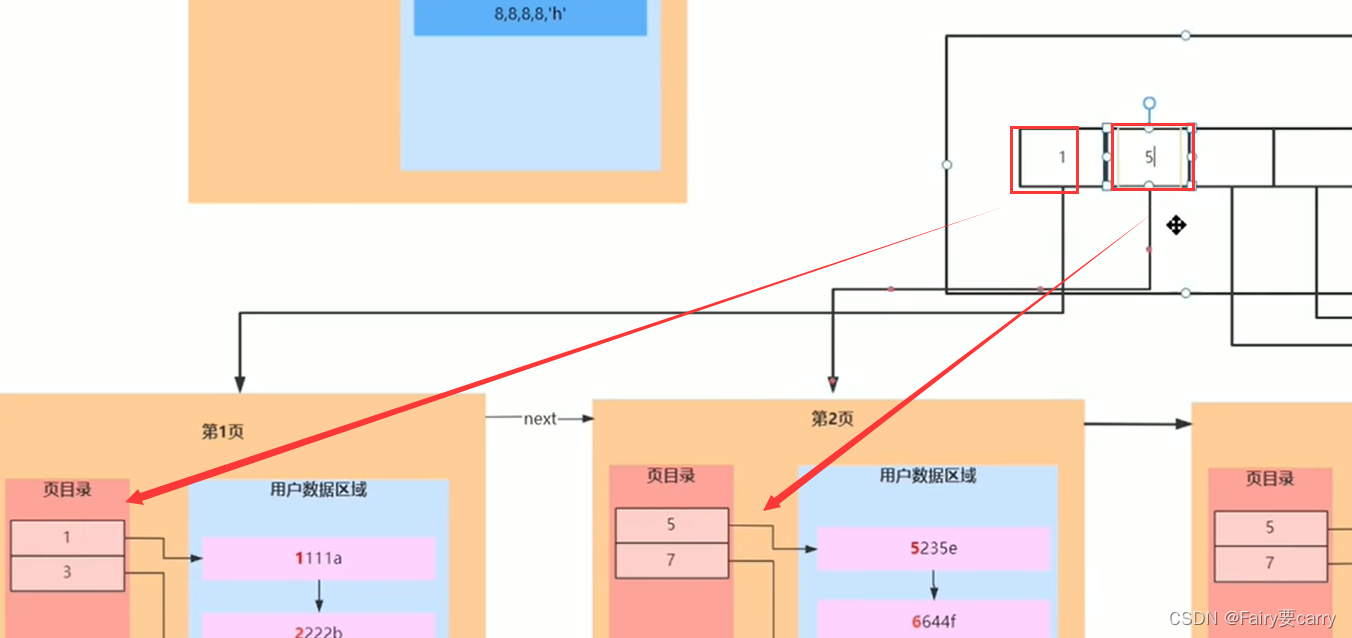
页目录优化
在创建一个目录,将每一页页目录中最小的主键放到这个目录里面,当我们进行搜索的时候可以先根据这个目录确定数据所在数据页,然后进而确定哪个位置
比如下面的你找主键id为3,就会根据主键值找到具体的数据页,然后再根据数据的页目录找到具体的用户数据
其实我们这个页目录就很像索引的建立
2.插入操作
https://zhuanlan.zhihu.com/p/149287061#:~:text=B%2B%E6%A0%91%E7%9A%84%E6%8F%92%E5%85%A5%E6%93%8D%E4%BD%9C%201%20%E6%8F%92%E5%85%A5%E7%9A%84%E6%93%8D%E4%BD%9C%E5%85%A8%E9%83%A8%E9%83%BD%E5%9C%A8%E5%8F%B6%E5%AD%90%E7%BB%93%E7%82%B9%E4%B8%8A%E8%BF%9B%E8%A1%8C%EF%BC%8C%E4%B8%94%E4%B8%8D%E8%83%BD%E7%A0%B4%E5%9D%8F%E5%85%B3%E9%94%AE%E5%AD%97%E8%87%AA%E5%B0%8F%E8%80%8C%E5%A4%A7%E7%9A%84%E9%A1%BA%E5%BA%8F%EF%BC%9B,2%20%E7%94%B1%E4%BA%8E%20B%2B%E6%A0%91%E4%B8%AD%E5%90%84%E7%BB%93%E7%82%B9%E4%B8%AD%E5%AD%98%E5%82%A8%E7%9A%84%E5%85%B3%E9%94%AE%E5%AD%97%E7%9A%84%E4%B8%AA%E6%95%B0%E6%9C%89%E6%98%8E%E7%A1%AE%E7%9A%84%E8%8C%83%E5%9B%B4%EF%BC%8C%E5%81%9A%E6%8F%92%E5%85%A5%E6%93%8D%E4%BD%9C%E5%8F%AF%E8%83%BD%E4%BC%9A%E5%87%BA%E7%8E%B0%E7%BB%93%E7%82%B9%E4%B8%AD%E5%85%B3%E9%94%AE%E5%AD%97%E4%B8%AA%E6%95%B0%E8%B6%85%E8%BF%87%E9%98%B6%E6%95%B0%E7%9A%84%E6%83%85%E5%86%B5%EF%BC%8C%E6%AD%A4%E6%97%B6%E9%9C%80%E8%A6%81%E5%B0%86%E8%AF%A5%E7%BB%93%E7%82%B9%E8%BF%9B%E8%A1%8C%20%E2%80%9C%E5%88%86%E8%A3%82%E2%80%9D%EF%BC%9B
在B+树中插入关键字时,需要注意以下几点:
1.插入的操作全部都在叶子结点上进行,且不能破坏关键字自小而大的顺序;
2.由于 B+树中各结点中存储的关键字的个数有明确的范围,做插入操作可能会出现结点中关键字个数超过阶数的情况,此时需要将该结点进行 “分裂”;
我们依旧以之前介绍查找操作时使用的图对插入操作进行说明,需要注意的是,B+树的阶数 M = 3 ,且 ⌈M/2⌉ = 2(取上限) 、⌊M/2⌋ = 1(取下限) :
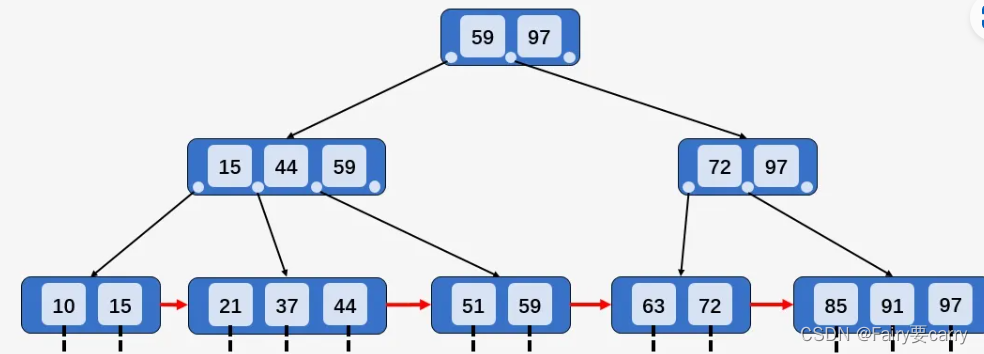
B+树中做插入关键字的操作,有以下 3 种情况:
1、 若被插入关键字所在的结点,其含有关键字数目小于阶数 M,则直接插入;
比如插入关键字 12 ,插入关键字所在的结点的 [10,15] 包含两个关键字,小于 M ,则直接插入关键字 12
2、 若被插入关键字所在的结点,其含有关键字数目等于阶数 M;
则需要将该结点分裂为两个结点,一个结点包含 ⌊M/2⌋ ,另一个结点包含 ⌈M/2⌉ 。同时,将⌈M/2⌉的关键字上移至其双亲结点。假设其双亲结点中包含的关键字个数小于 M,则插入操作完成。
插入关键字 95 ,插入关键字所在结点 [85、91、97] 包含 3 个关键字,等于阶数 M ,则将 [85、91、97] 分裂为两个结点 [85、91] 和结点 [97] , 关键字 95 插入到结点 [95、97] 中,并将关键字 91 上移至其双亲结点中,发现其双亲结点 [72、97] 中包含的关键字的个数 2 小于阶数 M ,插入操作完成
3、在第 2 情况中,如果上移操作导致其双亲结点中关键字个数大于 M,则应继续分裂其双亲结点。
插入关键字 40 ,按照第 2 种情况将结点分裂,并将关键字 37 上移到父结点,发现父结点 [15、37、44、59] 包含的关键字的个数大于 M ,所以将结点 [15、37、44、59] 分裂为两个结点 [15、37] 和结点 [44、59] ,并将关键字 37 上移到父结点中 [37、59、97] . 父结点包含关键字个数没有超过 M ,插入结束。
3.时间复杂度:
B+树插入删除时间复杂度为0(1)
搜索的时间复杂度为0(logn)
4.代码
package com.wyh.bootmath_java.Treap;
/**
* 实现B+树
*
* @param <T> 指定值类型
* @param <V> 使用泛型,指定索引类型,并且指定必须继承Comparable
*/
public class BPlusTree <T, V extends Comparable<V>>{
//B+树的阶
private Integer bTreeOrder;
//B+树的非叶子节点最小拥有的子节点数量(同时也是键的最小数量)
//private Integer minNUmber;
//B+树的非叶子节点最大拥有的节点数量(同时也是键的最大数量)
private Integer maxNumber;
private Node<T, V> root;
private LeafNode<T, V> left;
//无参构造方法,默认阶为3
public BPlusTree(){
this(3);
}
//有参构造方法,可以设定B+树的阶
public BPlusTree(Integer bTreeOrder){
this.bTreeOrder = bTreeOrder;
//this.minNUmber = (int) Math.ceil(1.0 * bTreeOrder / 2.0);
//因为插入节点过程中可能出现超过上限的情况,所以这里要加1
this.maxNumber = bTreeOrder + 1;
this.root = new LeafNode<T, V>();
this.left = null;
}
//查询
public T find(V key){
T t = this.root.find(key);
if(t == null){
System.out.println("不存在");
}
return t;
}
//插入
public void insert(T value, V key){
if(key == null)
return;
Node<T, V> t = this.root.insert(value, key);
if(t != null)
this.root = t;
this.left = (LeafNode<T, V>)this.root.refreshLeft();
// System.out.println("插入完成,当前根节点为:");
// for(int j = 0; j < this.root.number; j++) {
// System.out.print((V) this.root.keys[j] + " ");
// }
// System.out.println();
}
/**
* 节点父类,因为在B+树中,非叶子节点不用存储具体的数据,只需要把索引作为键就可以了
* 所以叶子节点和非叶子节点的类不太一样,但是又会公用一些方法,所以用Node类作为父类,
* 而且因为要互相调用一些公有方法,所以使用抽象类
*
* @param <T> 同BPlusTree
* @param <V>
*/
abstract class Node<T, V extends Comparable<V>>{
//父节点
protected Node<T, V> parent;
//子节点
protected Node<T, V>[] childs;
//键(子节点)数量
protected Integer number;
//键
protected Object keys[];
//构造方法
public Node(){
this.keys = new Object[maxNumber];
this.childs = new Node[maxNumber];
this.number = 0;
this.parent = null;
}
//查找
abstract T find(V key);
//插入
abstract Node<T, V> insert(T value, V key);
abstract LeafNode<T, V> refreshLeft();
}
/**
* 非叶节点类
* @param <T>
* @param <V>
*/
class BPlusNode <T, V extends Comparable<V>> extends Node<T, V>{
public BPlusNode() {
super();
}
/**
* 递归查找,这里只是为了确定值究竟在哪一块,真正的查找到叶子节点才会查
* @param key
* @return
*/
@Override
T find(V key) {
int i = 0;
while(i < this.number){
if(key.compareTo((V) this.keys[i]) <= 0)
break;
i++;
}
if(this.number == i)
return null;
return this.childs[i].find(key);
}
/**
* 递归插入,先把值插入到对应的叶子节点,最终讲调用叶子节点的插入类
* @param value
* @param key
*/
@Override
Node<T, V> insert(T value, V key) {
int i = 0;
while(i < this.number){
if(key.compareTo((V) this.keys[i]) < 0)
break;
i++;
}
if(key.compareTo((V) this.keys[this.number - 1]) >= 0) {
i--;
// if(this.childs[i].number + 1 <= bTreeOrder) {
// this.keys[this.number - 1] = key;
// }
}
// System.out.println("非叶子节点查找key: " + this.keys[i]);
return this.childs[i].insert(value, key);
}
@Override
LeafNode<T, V> refreshLeft() {
return this.childs[0].refreshLeft();
}
/**
* 当叶子节点插入成功完成分解时,递归地向父节点插入新的节点以保持平衡
* @param node1
* @param node2
* @param key
*/
Node<T, V> insertNode(Node<T, V> node1, Node<T, V> node2, V key){
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1]);
V oldKey = null;
if(this.number > 0)
oldKey = (V) this.keys[this.number - 1];
//如果原有key为null,说明这个非节点是空的,直接放入两个节点即可
if(key == null || this.number <= 0){
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1] + "直接插入");
this.keys[0] = node1.keys[node1.number - 1];
this.keys[1] = node2.keys[node2.number - 1];
this.childs[0] = node1;
this.childs[1] = node2;
this.number += 2;
return this;
}
//原有节点不为空,则应该先寻找原有节点的位置,然后将新的节点插入到原有节点中
int i = 0;
while(key.compareTo((V)this.keys[i]) != 0){
i++;
}
//左边节点的最大值可以直接插入,右边的要挪一挪再进行插入
this.keys[i] = node1.keys[node1.number - 1];
this.childs[i] = node1;
Object tempKeys[] = new Object[maxNumber];
Object tempChilds[] = new Node[maxNumber];
System.arraycopy(this.keys, 0, tempKeys, 0, i + 1);
System.arraycopy(this.childs, 0, tempChilds, 0, i + 1);
System.arraycopy(this.keys, i + 1, tempKeys, i + 2, this.number - i - 1);
System.arraycopy(this.childs, i + 1, tempChilds, i + 2, this.number - i - 1);
tempKeys[i + 1] = node2.keys[node2.number - 1];
tempChilds[i + 1] = node2;
this.number++;
//判断是否需要拆分
//如果不需要拆分,把数组复制回去,直接返回
if(this.number <= bTreeOrder){
System.arraycopy(tempKeys, 0, this.keys, 0, this.number);
System.arraycopy(tempChilds, 0, this.childs, 0, this.number);
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1] + ", 不需要拆分");
return null;
}
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1] + ",需要拆分");
//如果需要拆分,和拆叶子节点时类似,从中间拆开
Integer middle = this.number / 2;
//新建非叶子节点,作为拆分的右半部分
BPlusNode<T, V> tempNode = new BPlusNode<T, V>();
//非叶节点拆分后应该将其子节点的父节点指针更新为正确的指针
tempNode.number = this.number - middle;
tempNode.parent = this.parent;
//如果父节点为空,则新建一个非叶子节点作为父节点,并且让拆分成功的两个非叶子节点的指针指向父节点
if(this.parent == null) {
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1] + ",新建父节点");
BPlusNode<T, V> tempBPlusNode = new BPlusNode<>();
tempNode.parent = tempBPlusNode;
this.parent = tempBPlusNode;
oldKey = null;
}
System.arraycopy(tempKeys, middle, tempNode.keys, 0, tempNode.number);
System.arraycopy(tempChilds, middle, tempNode.childs, 0, tempNode.number);
for(int j = 0; j < tempNode.number; j++){
tempNode.childs[j].parent = tempNode;
}
//让原有非叶子节点作为左边节点
this.number = middle;
this.keys = new Object[maxNumber];
this.childs = new Node[maxNumber];
System.arraycopy(tempKeys, 0, this.keys, 0, middle);
System.arraycopy(tempChilds, 0, this.childs, 0, middle);
//叶子节点拆分成功后,需要把新生成的节点插入父节点
BPlusNode<T, V> parentNode = (BPlusNode<T, V>)this.parent;
return parentNode.insertNode(this, tempNode, oldKey);
}
}
/**
* 叶节点类
* @param <T>
* @param <V>
*/
class LeafNode <T, V extends Comparable<V>> extends Node<T, V> {
protected Object values[];
protected LeafNode left;
protected LeafNode right;
public LeafNode(){
super();
this.values = new Object[maxNumber];
this.left = null;
this.right = null;
}
/**
* 进行查找,经典二分查找,不多加注释
* @param key
* @return
*/
@Override
T find(V key) {
if(this.number <=0)
return null;
// System.out.println("叶子节点查找");
Integer left = 0;
Integer right = this.number;
Integer middle = (left + right) / 2;
while(left < right){
V middleKey = (V) this.keys[middle];
if(key.compareTo(middleKey) == 0)
return (T) this.values[middle];
else if(key.compareTo(middleKey) < 0)
right = middle;
else
left = middle;
middle = (left + right) / 2;
}
return null;
}
/**
*
* @param value
* @param key
*/
@Override
Node<T, V> insert(T value, V key) {
// System.out.println("叶子节点,插入key: " + key);
//保存原始存在父节点的key值
V oldKey = null;
if(this.number > 0)
oldKey = (V) this.keys[this.number - 1];
//先插入数据
int i = 0;
while(i < this.number){
if(key.compareTo((V) this.keys[i]) < 0)
break;
i++;
}
//复制数组,完成添加
Object tempKeys[] = new Object[maxNumber];
Object tempValues[] = new Object[maxNumber];
System.arraycopy(this.keys, 0, tempKeys, 0, i);
System.arraycopy(this.values, 0, tempValues, 0, i);
System.arraycopy(this.keys, i, tempKeys, i + 1, this.number - i);
System.arraycopy(this.values, i, tempValues, i + 1, this.number - i);
tempKeys[i] = key;
tempValues[i] = value;
this.number++;
// System.out.println("插入完成,当前节点key为:");
// for(int j = 0; j < this.number; j++)
// System.out.print(tempKeys[j] + " ");
// System.out.println();
//判断是否需要拆分
//如果不需要拆分完成复制后直接返回
if(this.number <= bTreeOrder){
System.arraycopy(tempKeys, 0, this.keys, 0, this.number);
System.arraycopy(tempValues, 0, this.values, 0, this.number);
//有可能虽然没有节点分裂,但是实际上插入的值大于了原来的最大值,所以所有父节点的边界值都要进行更新
Node node = this;
while (node.parent != null){
V tempkey = (V)node.keys[node.number - 1];
if(tempkey.compareTo((V)node.parent.keys[node.parent.number - 1]) > 0){
node.parent.keys[node.parent.number - 1] = tempkey;
node = node.parent;
}
else {
break;
}
}
// System.out.println("叶子节点,插入key: " + key + ",不需要拆分");
return null;
}
// System.out.println("叶子节点,插入key: " + key + ",需要拆分");
//如果需要拆分,则从中间把节点拆分差不多的两部分
Integer middle = this.number / 2;
//新建叶子节点,作为拆分的右半部分
LeafNode<T, V> tempNode = new LeafNode<T, V>();
tempNode.number = this.number - middle;
tempNode.parent = this.parent;
//如果父节点为空,则新建一个非叶子节点作为父节点,并且让拆分成功的两个叶子节点的指针指向父节点
if(this.parent == null) {
// System.out.println("叶子节点,插入key: " + key + ",父节点为空 新建父节点");
BPlusNode<T, V> tempBPlusNode = new BPlusNode<>();
tempNode.parent = tempBPlusNode;
this.parent = tempBPlusNode;
oldKey = null;
}
System.arraycopy(tempKeys, middle, tempNode.keys, 0, tempNode.number);
System.arraycopy(tempValues, middle, tempNode.values, 0, tempNode.number);
//让原有叶子节点作为拆分的左半部分
this.number = middle;
this.keys = new Object[maxNumber];
this.values = new Object[maxNumber];
System.arraycopy(tempKeys, 0, this.keys, 0, middle);
System.arraycopy(tempValues, 0, this.values, 0, middle);
this.right = tempNode;
tempNode.left = this;
//叶子节点拆分成功后,需要把新生成的节点插入父节点
BPlusNode<T, V> parentNode = (BPlusNode<T, V>)this.parent;
return parentNode.insertNode(this, tempNode, oldKey);
}
@Override
LeafNode<T, V> refreshLeft() {
if(this.number <= 0)
return null;
return this;
}
}
}