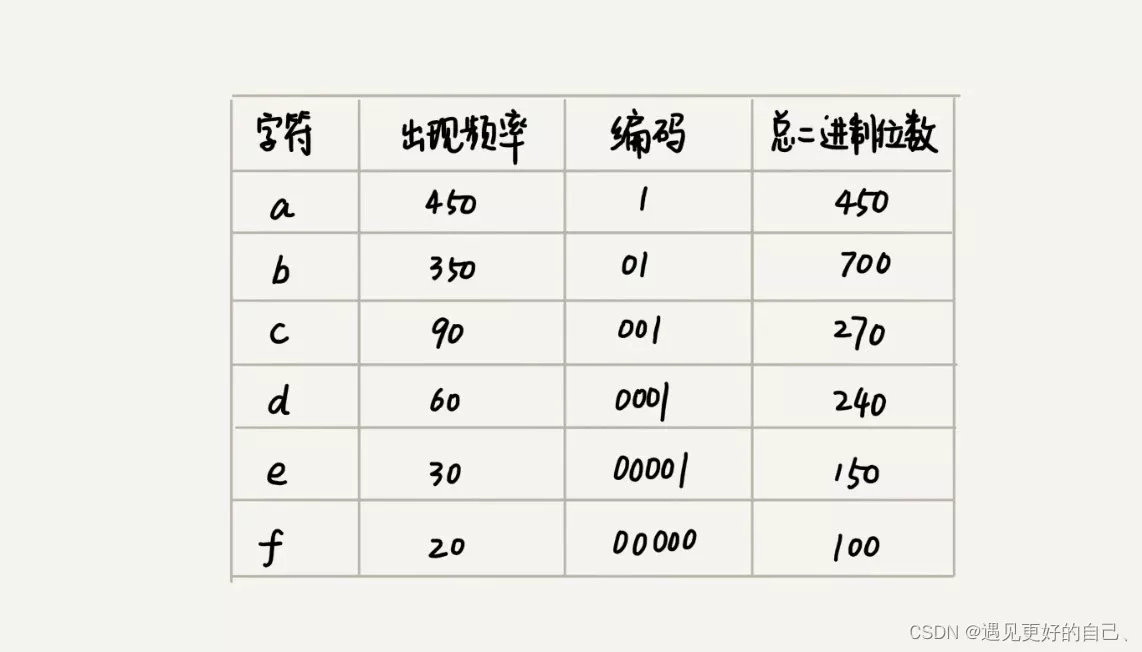
1.给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？

如何找到top K的IP？

思路：（哈希切割）

1.ip本身就是一个字符串，先把ip变成一个整数hash(ip)

2.文件的下标index = hash(ip) % 200 (把相同的字符串映射到同一个文件当中去)

3.读取每个文件的内容，统计每个文件当中，ip出现的次数。用hashmap

2.给定100亿个整数，设计算法找到只出现一次的整数？

思路：

解法一（哈希切割）

把数字哈希到对应的小文件当中，一样的数字肯定是在一起的，遍历每个小文件，统计数字出现的次数，此时，在内存中就能够知道，哪个数字出现了一次。

解法二（位图）

10 000 000 000 * 4 / 1024 / 1024 ~= 38,146.972M ~= 37.25G

100亿个整数用到位图大约10 000 000 000/8/1024/1024 ~= 1192.092M  ~= 1G

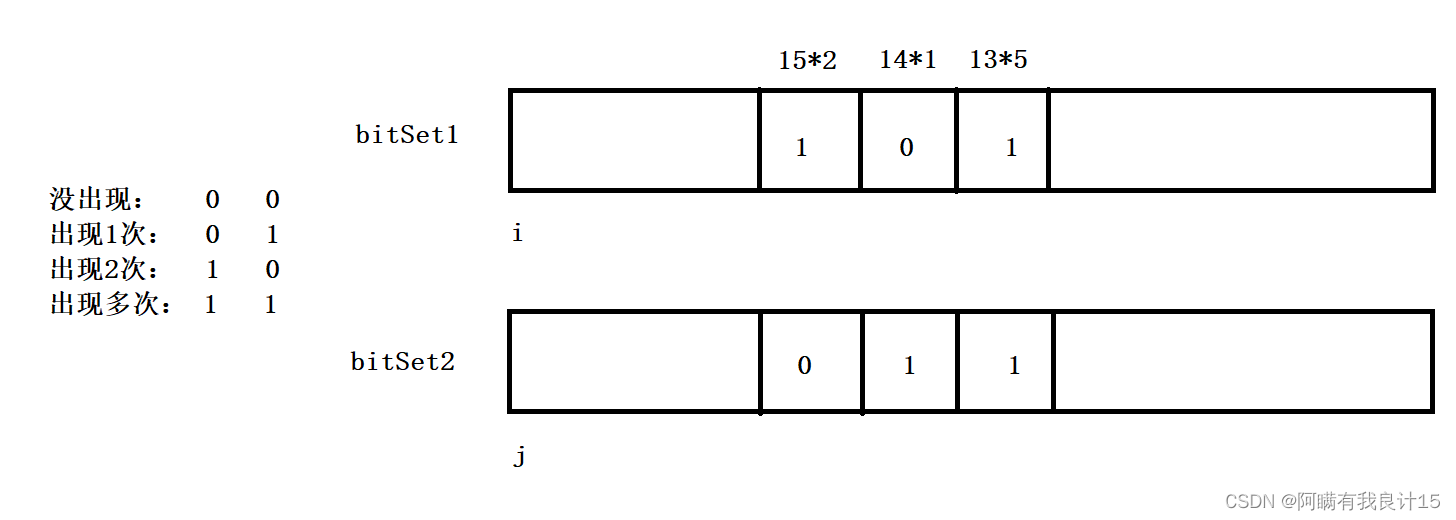
 解法三（使用一个位图）

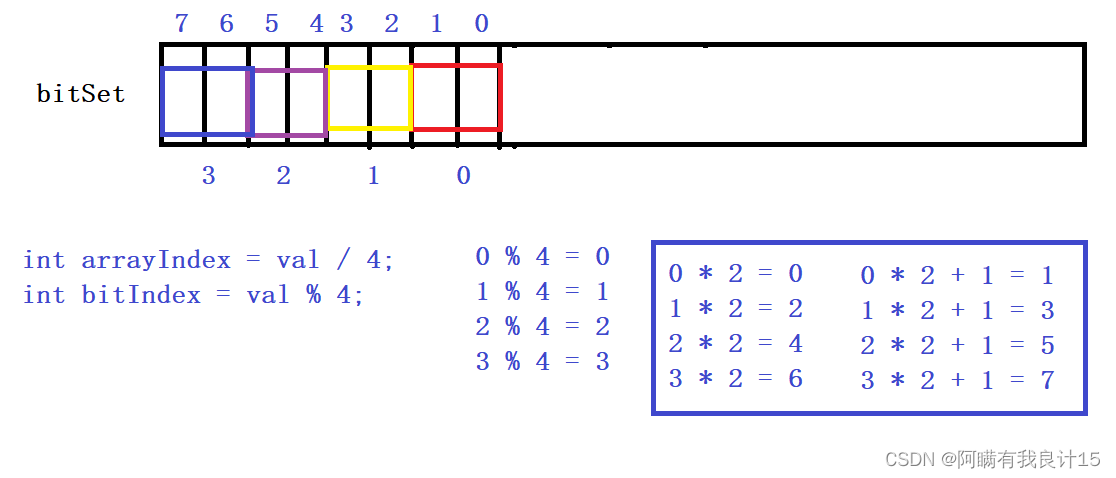
 和第二种解法一样，都能用0,1标识出现几次，这属于编码细节了，总体思路就是原来能表示8个数据，现在用俩个比特位标识。原来需要1个G,现在用这种方法得用2个G.

3. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

解法一：（哈希切割）

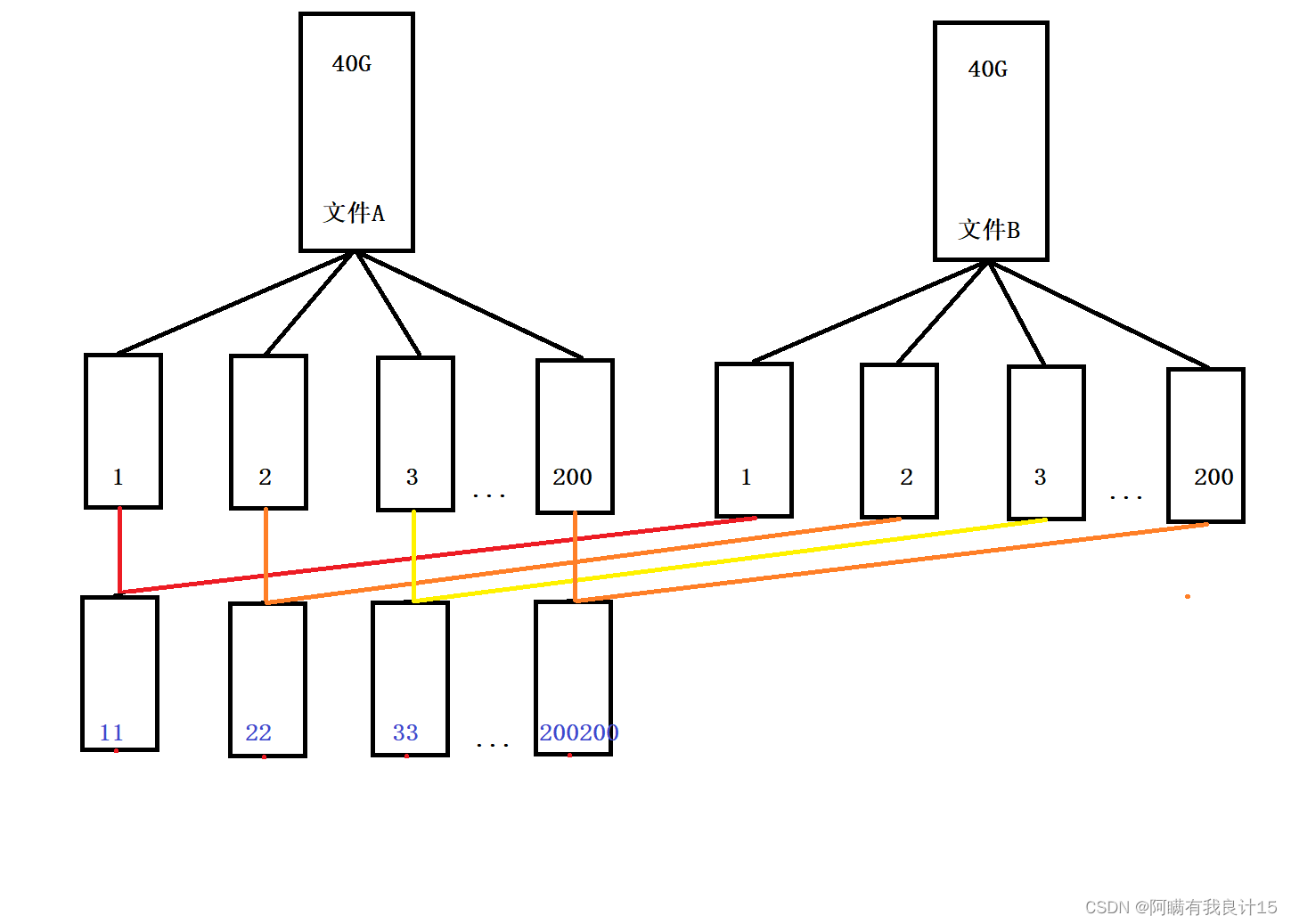
解法二：（位图）

 1.和上边第一步一样，先把40G文件分成200份小文件

2.遍历A文件的第一个文件，将第一个文件数据读取出来，存放到bitSet当中

3.遍历B文件的第一个文件，每次读取一个数据，看bitSet中，之前是否存在

4.如果存在，就是交集

如何求交集，并集，差集？

 

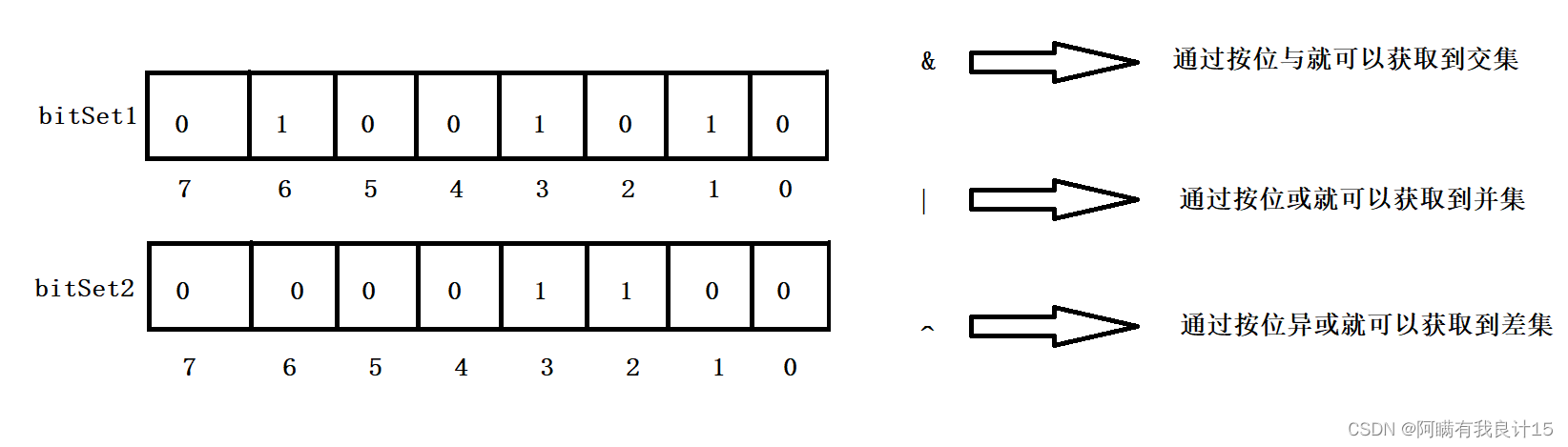
4. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

解法一（哈希切割）

解法二（位图）

用俩个bitSet,00代表0次，01代表1次，10代表2次，11代表多次，和第二题解法一样

5.给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法

1.精确算法：

哈希切割，和第三题一样

2.近似算法：

1.把第一个文件当中的query映射到布隆过滤器中

2.读取第二个文件，每个query，都去布隆过滤器中查找【会存在误判】

3.因为存在误判，所以有可能这个数据存在，但是误判成了不存在。