由数据范围反推算法复杂度以及算法内容 - AcWing
常用代码模板3——搜索与图论 - AcWing
基本思想:
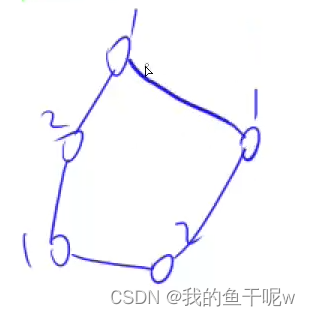
二分图:在一张图中,如果能把全部点分到两个集合,且保证两个集合内部没有任何一条边,图中的边只存在于两个集合之间,那么这张图就是二分图。
这里我们主要介绍染色法(一般用来判定二分图)和匈牙利算法(一般用来计算二分图的最大匹配数)。染色法就是用两种不同的颜色对图中的点进行染色,一个点显然不能具有两种颜色,所以如果出现这样的点,该图就不是二分图,即图中不包含奇数环;匈牙利算法是两个集合分别选一个点,两个点之间有边就确定一条关系,如果某个点的关系被确定了,他会先去看上一个点能否换其他点,如果不能,该点再去找别的点,最后得出的最多的关系数量就是最大匹配数。
860. 染色法判定二分图 - AcWing题库
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环。
请你判断这个图是否是二分图。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示点 u 和点 v 之间存在一条边。
输出格式
如果给定图是二分图,则输出 Yes,否则输出 No。
数据范围
1≤n,m≤1e5
输入样例:
4 4
1 3
1 4
2 3
2 4
输出样例:
Yes
#include<iostream> #include<algorithm> #include<cstring> using namespace std; const int N = 100010, M = 200010;//因为是存的无向图,数组就要开两倍才够用 int h[N], e[M], ne[M], idx; int color[N]; int n, m; void add(int a, int b) { e[idx] = b; ne[idx] = h[a]; h[a] = idx++; } bool dfs(int u, int c) { color[u] = c; for(int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if(!color[j]) { if(!dfs(j, 3 - c)) return false; } else if(color[j] == c) return false; } return true; } int main() { memset(h, -1, sizeof h); cin >> n >> m; while(m--) { int a, b; cin >> a >> b; add(a, b); add(b, a); } bool flag = true; for(int i = 1; i <= n; i++) { if(!color[i]) { if(!dfs(i, 1)) { flag = false; break; } } } if(flag) cout << "Yes"; else cout << "No"; return 0; }
861. 二分图的最大匹配 - AcWing题库
给定一个二分图,其中左半部包含 n1 个点(编号 1∼n1),右半部包含 n2 个点(编号 1∼n2),二分图共包含 m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
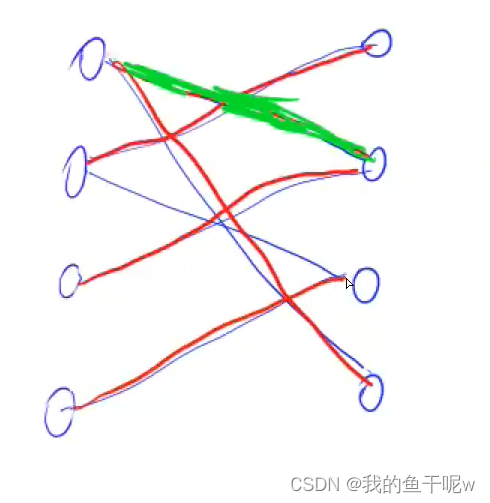
二分图的匹配:给定一个二分图 G,在 G 的一个子图 M 中,M 的边集 {E} 中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
输入格式
第一行包含三个整数 n1、 n2 和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示左半部点集中的点 u 和右半部点集中的点 v 之间存在一条边。
输出格式
输出一个整数,表示二分图的最大匹配数。
数据范围
1≤n1,n2≤500,
1≤u≤n1,
1≤v≤n2,
1≤m≤1e5,
输入样例:
2 2 4
1 1
1 2
2 1
2 2
输出样例:
2#include<iostream> #include<algorithm> #include<cstring> using namespace std; const int N = 100010, M = 200010; int n1, n2, m; int h[N], e[M], ne[M], idx; int match[N];//右边的点所对应的左边的点 bool st[N];//判重 避免重复搜索某一个点 void add(int a, int b) { e[idx] = b; ne[idx] = h[a]; h[a] = idx++; } bool find(int x) { for(int i = h[x]; ~i; i = ne[i]) { int j = e[i]; if(!st[j]) { st[j] = true; if(match[j] == 0 || find(match[j]))//左边的点连接的右边的点没有遍历 //或者该点所连的左边的点能换另一个点连接,那么目前左边的点就能与右边的该点链接 { match[j] = x; return true; } } } return false; } int main() { memset(h, -1, sizeof h); cin >> n1 >> n2 >> m; while(m--) { int a, b; cin >> a >> b; add(a, b); } int res = 0; for(int i = 1; i <= n1; i++)//遍历左边每一个点 { memset(st, false, sizeof st); if(find(i)) res++; } cout << res; return 0; }