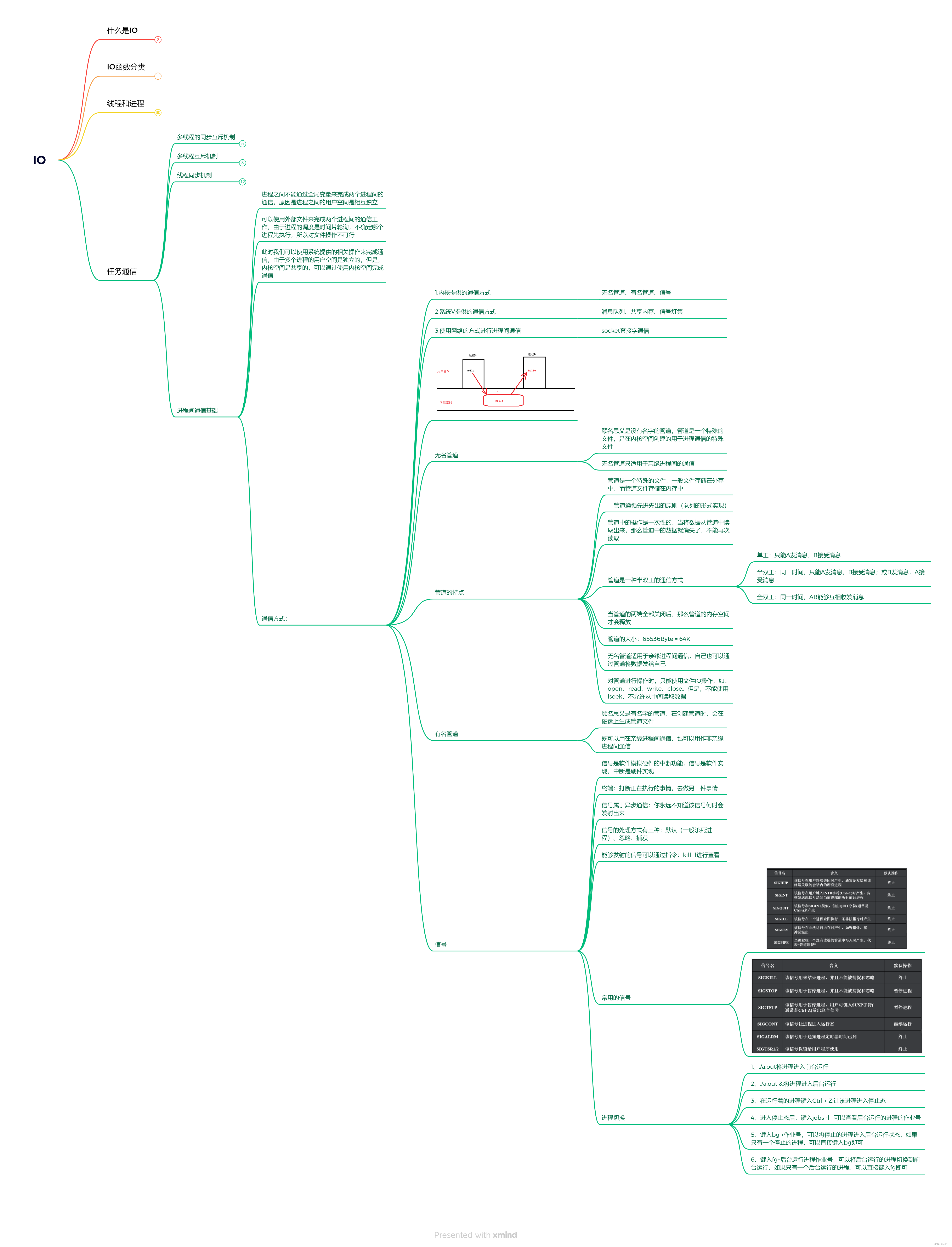
343.整数拆分

题目：
给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
题目链接：343.整数拆分
解题思路：
dp是数字n拆分后的最大乘积
递推公式 首先拆成两个数字 数字j可以拆成i ，j-i i可以继续拆 所以可以在dp[i]j-i与in-i中取最值
i*dp[i-j] 将其拆为至少是三个数
代码如下：

/初始化dp数组明白含义 正整数n拆分后的最大乘积
//确定递推公式
//初始化 dp[2]=1;
//确定遍历
class Solution {
    public int integerBreak(int n) {
        //特殊情况
        if(n==1||n==0){
            return 0;
        }
        int dp[]=new int[n+1];
        //初始化
        dp[2]=1;
        for(int i=3;i<=n;i++){
            for(int j=1;j<i;j++){
                //j*i-j 将其拆为两个数
                //j*dp[i-j] 将其拆为至少是三个数
                //*** */dp[i] 保留拆数不同结果的最大数
                
                dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));
            }
        }
        return dp[n];
    }
}

96.不同的二叉搜索树

题目：
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

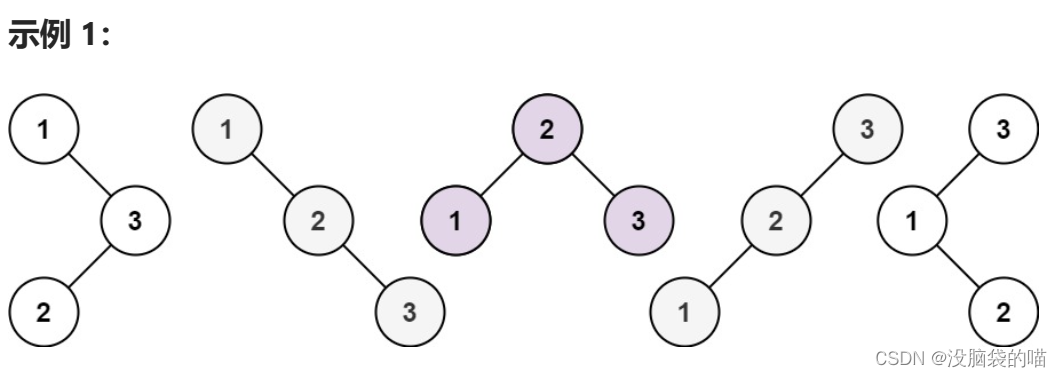
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1
代码如下：

//动规五部曲
//确定dp数组的含义 dp[i] 为 n=i时，不同搜索二叉树有多少种
//初始化 dp[0]=1 dp[1]=1 dp[2]=2
//遍历
//当n为3时，总数为头节点为1-3的个数的总和
//当头节点为1时，左边有0个子节点，右边有2个 个数=dp[0]*
//当头节点为2时，左边有1个子节点，右边有1个
//当头节点为3时，左边有2个子节点，右边有0个
class Solution {
    public int numTrees(int n) {
        int dp[]=new int[n+1];
        dp[0]=1;
        dp[1]=1;
        if(n <= 1){
            return dp[n];    
        }
        for(int temp=2;temp<=n;temp++){
            for(int i=0;i<temp;i++){
                dp[temp]+=dp[i]*dp[temp-1-i];
            }
        }
        return dp[n];
    }
}

进阶：
95. 不同的二叉搜索树 II

//动规解法
//dp数组的含义：dp[i]dp[i]dp[i]表示序列[1,2,3,...,i][1,2,3,...,i][1,2,3,...,i]能够形成的所有不同BST
//初始化：i=0 时为空树，i=1时为只有一个根节点1的树
class Solution {
    //深拷贝!!太精彩了
    TreeNode copyTree(TreeNode tmp,int j){
        if(tmp==null){
            return null;
        }
        TreeNode left=copyTree(tmp.left,j);
        TreeNode right=copyTree(tmp.right,j);
        TreeNode node=new TreeNode(tmp.val+j,left,right);
        return node;
    }
    public List<TreeNode> generateTrees(int n) {
        List<List<TreeNode>> dp=new ArrayList<>();
        ArrayList first=new ArrayList<>();
        first.add(null);
        dp.add(first);
        if(n>0){
            ArrayList second=new ArrayList<>();
            second.add(new TreeNode(1));
            dp.add(second);
        }
        for(int i=2;i<=n;i++){
            ArrayList res=new ArrayList<>();
            for(int j=1;j<=i;j++){
                //以j为中间结点的不同的右子树
                for(TreeNode right:dp.get(i-j)){
                    TreeNode rchild=copyTree(right,j);
                    for(TreeNode left:dp.get(j-1)){
                        TreeNode root =new TreeNode(j);
                        root.left=left;
                        root.right=rchild;
                        res.add(root);
                    }
                }
                
            }
            dp.add(res);
        }
        return dp.get(dp.size()-1);
    }
   
}