代码随想录算法训练营第二十六天 | LeetCode 39. 组合总和、40. 组合总和 II、131. 分割回文串

文章链接：组合总和组合总和II 分割回文串

视频链接：组合总和组合总和II 分割回文串

1. LeetCode 39. 组合总和

1.1 思路

1.2 代码

2. LeetCode 40. 组合总和 II

2.1 思路

2.2 代码

3. LeetCode 131. 分割回文串

3.1 思路

3.2 代码

1. LeetCode 39. 组合总和

1.1 思路

这题跟上面那些组合的题目的区别在于可以重复取数，而且这题抽象出来的树形结构的深度是由和来限定的。这里我们举例，数组[2,5,3]，和为4，那么我们取了2之后，子集合是[2,5,3]，因为可以重复取数，后续接着取。然后如果在第一层取5时（此时取2的路径已经走完了），子集合就是[5,3]了，这时如果再把2带上就会得到重复的组合，这也是startIndex控制的地方。这题和上面做个的类似组合问题的差别就是子集合是把已经选过的元素带上的，这样才可达到可重复选取的目的
定义两个全局变量，二维数组result存最终结果，path存放当前的单次结果。
回溯算法的返回值和参数：返回值void，参数candidates，target，sum统计path里的和，startIndex控制子集合的初始位置
终止条件：如果sum>target就return；如果sum==target就把path加入result中，然后return
单层搜索的逻辑：for循环(int i=startIndex; i<candidates.length; i++)。
注意：这里的for循环中startIndex第一次传入时是从0开始的，就是大家最常见的数组遍历方式，为什么与上面做过的那些组合的for循环不一样呢？因为上面的题取的元素都是1到9这样子的，要从1开始取之类的，而本题的数组遍历是通过下标遍历的，因此有点不一样
接上述的for循环，然后path.add(数组[i])；sum+=数组[i]；然后就递归的过程backtracking(candidates, target, sum, i)。注意这里传入的是i不是startIndex，因为传入startIndex就会一直是0，而i会在for循环里递增，那样才是正确的遍历顺序。而这里不用i+1就是可以重复取数的关键，下一层递归依然可以取同一个数
然后是回溯的过程，path.removeLast()去除最后一个元素也就是刚刚加入的元素，这样才能往树的右边搜索，并且sum-=数组[i]
剪枝优化：通常是在for循环里做文章的，剪枝就是剪去多余的分支，分支就体现在for循环上，原理就是让其少循环，上述的sum>target就是不进入循环，下面的方式就是提前退出循环。对于本题，还是上面的例子[2 ,5, 3]，先取出2和5发现已经大于4了，如果我们先排序数组，变成[2, 3, 5]那么取到2和3发现已经大于4了，那么后续的5就可以不用去搜索了。
这个操作就是写在for循环里的，如果sum+数组[i]>target了就直接break跳出循环，这就是把此树右边的分支剪去了。

1.2 代码

//
// 剪枝优化
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(candidates); // 先进行排序
        backtracking(res, new ArrayList<>(), candidates, target, 0, 0);
        return res;
    }

    public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {
        // 找到了数字和为 target 的组合
        if (sum == target) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = idx; i < candidates.length; i++) {
            // 如果 sum + candidates[i] > target 就终止遍历
            if (sum + candidates[i] > target) break;
            path.add(candidates[i]);
            backtracking(res, path, candidates, target, sum + candidates[i], i);
            path.remove(path.size() - 1); // 回溯，移除路径 path 最后一个元素
        }
    }
}

2. LeetCode 40. 组合总和 II

2.1 思路

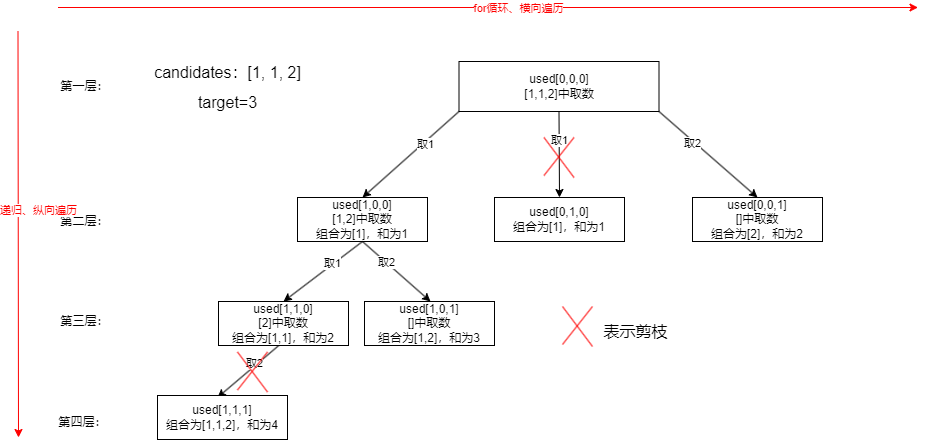
这题和上述的组合类的题目的区别在于题目给的数组是有重复元素的，上面做过的是没有的，而且题目要求组合中不可以有重复的组合，即答案里的数组可以出现[1,1,6]但不同出现[1,1,6],[1,1,6]，因此要去重
举个例子，数组[10, 1, 2, 7, 6, 1, 5]，和为8，这里就会出现两个1和7组成组合然后和为8，因此要做去重，而且题目要求同一个元素在单个组合中只能使用一次。大逻辑就是取过的元素就不要再取了（好像是废话）。
本题科普两个概念：树层去重，树枝去重。我们要考虑这两个维度，从这两个上考虑去重
我们需要定义一个boolean数组used，长度和题目给的数组是一样大的，如果对应下标的数组元素使用过就定义为true否则为false。再举个例子如上图所示，排好序的数组[1, 1, 2]，和为3。取1后used[0]=true，子集合为[1, 2]，以此类推，同样需要startIndex控制起始位置，for循环往右搜索的过程，起始位置都是不断+1的，只是我们要用used标记取过的数为true
树枝去重：树枝上我们第一层取了1之后，第二层也是可以取1的，这两个1不会是同一个元素的，因为传入的是i+1
树层去重：树层上我们左边第一个分支取1了，第二个分支还取1虽然不是同一个元素的，但是我们都是从这个1后面开始取的，也就是比如[1, 1, 2,......]这里的第一个1和第二个1虽然不同，但是后面的是相同的，我们可能取后面的元素，就可能重复了。因此关键在树层去重
定义两个全局变量result存放全部结果、path存放单个结果
回溯函数的参数和返回值：返回值void，参数candidates，target，sum计算path里的和，startIndex控制子集合的起始位置，为了防止组合里出现重复元素，boolean数组used标记哪个元素用过。不过我们在进入这个回溯函数之前要在主函数先给数组排序，因为去重是在这个前提下进行的
终止条件：如果sum>target就return。如果sum==target就把path加入result中，然后return
单层搜索的逻辑：for(int i=startIndex;i<candidates.length;i++)。首先是树层去重的逻辑，如果（i>0&&candidates[i]==candidates[i-1]&&!used[i-1]）避免i-1为负数，首先要求i>0，然后是如果前后两个元素相等了就不能再取了，不然就重复了，然后下一个条件是前一个元素不能用过，这里是为了往下递归时，举例，取了一个1后，还能取多个1，这里的多个1不是同一个1，只是数值相同，这个条件不是为了树层去重的，而是为了取数找到结果。如果符合条件就continue跳过此次循环，继续往后取。
然后就是继续收集元素的过程path.add(数组[i])；sum+=数组[i]，used[i]=true；然后就递归的过程backtracking(candidates, target, sum, i+1, used)。然后就是回溯的过程，path.removeLast()去除最后一个元素也就是刚刚加入的元素，这样才能往树的右边搜索，并且sum-=数组[i]，used[i]=false。这里又变为false是为了往右搜索，逻辑和第一层往右搜索的原因是一样的

2.2 代码

//
class Solution {
  LinkedList<Integer> path = new LinkedList<>();
  List<List<Integer>> ans = new ArrayList<>();
  boolean[] used;
  int sum = 0;

  public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    used = new boolean[candidates.length];
    // 加标志数组，用来辅助判断同层节点是否已经遍历
    Arrays.fill(used, false);
    // 为了将重复的数字都放到一起，所以先进行排序
    Arrays.sort(candidates);
    backTracking(candidates, target, 0);
    return ans;
  }

  private void backTracking(int[] candidates, int target, int startIndex) {
    if (sum == target) {
      ans.add(new ArrayList(path));
    }
    for (int i = startIndex; i < candidates.length; i++) {
      if (sum + candidates[i] > target) {
        break;
      }
      // 出现重复节点，同层的第一个节点已经被访问过，所以直接跳过
      if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
        continue;
      }
      used[i] = true;
      sum += candidates[i];
      path.add(candidates[i]);
      // 每个节点仅能选择一次，所以从下一位开始
      backTracking(candidates, target, i + 1);
      used[i] = false;
      sum -= candidates[i];
      path.removeLast();
    }
  }
}

3. LeetCode 131. 分割回文串

3.1 思路

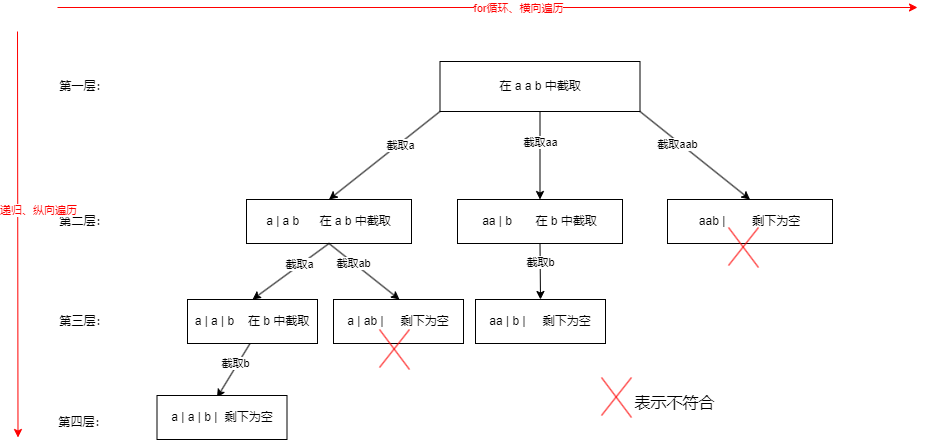
大概是分两步，先求出所有分割后的结果，在叶子节点的位置，然后在这个位置判断是否都是回文
回溯函数的参数和返回值：返回值void。要先定义两个全局变量，一维数组path收集路径即单个结果，存放的是字符串，二维数组result收集全部结果。函数参数：字符串s，startIndex控制取了一个字符后，剩下的要在这个字符后面的字符串中取
终止条件：上面参数startIndex就相当于我们图里画是那条切割的竖线“|”，当这条线“|”到了最后的位置说明到叶子节点了，也就是要处理的结果了。if(startIndex==s.length())就是到了叶子节点，然后result里加入path。我们这里是把判断是否回文的逻辑放在了“单层搜索的逻辑”中了，如果不是回文就不会进行下一层的递归
单层搜索的逻辑：for(int i=startIndex;i<s.length();i++)，这里我们要先判断切割的子串是否为回文串，是才加入到path。上面说过startIndex就是我们切割的线，那么[startIndex，i]这个左闭右闭的区间，就是切割的子串。这里startIndex在for循环里是一个固定的值，i是不断++的，因此他们之间的范围包括两端就是我们要搜索的范围。
这里定义个函数isPalindrome(s, startIndex, end)分别表示字符串，起始位置，终止位置，来判断这个区间内是否是回文的。如果是回文的，就path.add(子串)，否则就continue跳过此次循环。
然后是递归的逻辑backtracking(s，i+1)为什么i+1是因为切割过的不能重复切割。然后是回溯的过程，path.removeLast()，继续向右搜索。
判断函数就是用双指针，同时向中间遍历，如果都相等就是回文子串

3.2 代码

//
class Solution {
    List<List<String>> lists = new ArrayList<>();
    Deque<String> deque = new LinkedList<>();

    public List<List<String>> partition(String s) {
        backTracking(s, 0);
        return lists;
    }

    private void backTracking(String s, int startIndex) {
        //如果起始位置大于s的大小，说明找到了一组分割方案
        if (startIndex >= s.length()) {
            lists.add(new ArrayList(deque));
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            //如果是回文子串，则记录
            if (isPalindrome(s, startIndex, i)) {
                String str = s.substring(startIndex, i + 1);
                deque.addLast(str);
            } else {
                continue;
            }
            //起始位置后移，保证不重复
            backTracking(s, i + 1);
            deque.removeLast();
        }
    }
    //判断是否是回文串
    private boolean isPalindrome(String s, int startIndex, int end) {
        for (int i = startIndex, j = end; i < j; i++, j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        return true;
    }
}