前言

正则路径查询（Regular Path Query, RPQ）为带标签的图数据上重要的查询类型之一，旨在找出由至少一条满足条件的路径相连接的结点对，其中需满足的条件以正则表达式表达。当前对 RPQ 的研究以提升查询效率为目的，主要关注两方面：一是建何种索引，二是使用何种查询计划。本文将从这两方面入手，对当前最前沿的 RPQ 相关工作进行简要介绍。

问题定义

给定一张边上带标签的有向图、一个以边上标签为字母表的正则表达式，RPQ 要求返回所有由至少一条满足正则表达式的路径所连接的结点对，其中满足正则表达式指路径中边标签依次连接而成的字符串在该表达式给定的语言中。

本文仅考虑不使用硬件加速技巧的串行精确算法。

索引

RPQ 索引存储某些正则表达式在当前图上的查询结果（可能在此基础上进行压缩），其动机为期望查询中的正则表达式包含索引所存储的，则可避免在原图中搜索、只需读取索引就能得到该部分结果。

索引选取的方法分根据查询负载和根据图数据两类。

• 根据查询负载的方法：假设在开始查询之前，能够获取负载（即一个作为参考的查询集合，后续查询全部或几乎全属于此集合）。这类方法将索引选取视作一个优化问题。一些方法将最小化索引的空间占用作为优化目标：[13] 给出了一个精确的最优化算法，但其复杂度较高，需要调用一个 PSPACE 完全的子例程指数次；[5] 给出了一种贪心算法，在预先建立多种索引、以它们为基础运行部分示例查询的基础上，贪心地选择查询加速比-空间开销比率最高的索引，直至内存空间耗尽。
• 根据图数据的方法：此类方法选择图中部分满足条件的路径来建索引。[6] 对所有能形成 2 跳路径的边标签的 Kleene 闭包（如 $a^{\ast }$）建索引；[3] 对所有至多 k 跳路径的边标签序列建索引（其中 k 为参数）；[4] 对所有至多 k 跳的频繁路径的边标签序列建索引。

不论以何种方法选取，所建的索引均可分为两类：针对 Kleene 闭包的索引，和针对其他类型正则表达式的索引（其中可包含 Kleene 闭包，但最外层运算符非 *）。

针对 Kleene 闭包的索引包括：（仅介绍当前实验表现最优的工作，下同）

• DLCR [1]：可对形如 $(a_1|a_2|\cdots |a_k{)}^{\ast }$ 的 Kleene 闭包建索引。索引结构为添加了边标签信息的两跳标签（2-hop labeling），对于每个结点 v 有 $L_{out}(v)$ 和 $L_{in}(v)$ 两个集合，其中每个条目包含一个结点 s 和标签集合 ${\Psi }_s$ ，表示 v 通过边上标签集合包含于 ${\Psi }_s$ 的路径可达 s （对于 $L_{in}(v)$ ，表示 s 通过这样的路径可达 v）；这样的索引具有全局健全性（soundness）和完整性（completeness），即可以保证 u, v 为这种形式的 Kleene 闭包的 RPQ 查询结果当且仅当 $L_{out}(u)$ 和 $L_{in}(v)$ 中包含关于某个公共结点 s 的条目，且对应的 ${\Psi }_s$ 均包含于 { a 1 , a 2 , ⋯   , a k } \{a_1, a_2, \cdots, a_k\} {a1​,a2​,⋯,ak​} 。索引构建算法为从每个结点出发的正向和反向标签约束的广度优先搜索（Label-Constrained BFS, LC-BFS），对每个访问到的结点添加由 LC-BFS 起始结点和所走的路径相对应的索引条目；在添加新的条目前，首先检查当前已有的条目是否能推断出此条目，若能则不再添加，以保证索引的全局极小性（minimality），减小空间开销。
• RTC [2]：可对任意 Kleene 闭包（以下用 $R^{\ast }$ 表示）建索引。索引结构为缩减（reduce）后图的传递闭包矩阵。索引构建算法对图依次做以下两种缩减操作：边级别缩减，即将满足 $R$ 的路径缩为一条边；结点级别缩减，即将上一步缩减得到的图中的每个强连通分量缩为一个结点。最终计算此缩减图的传递闭包；传递闭包矩阵中为 1 的元素对应的结点对在原图中通过满足 $R^{\ast }$ 的路径可达。
• RDF-3X [6] ：可对形如 $(a_1|a_2|\cdots |a_k{)}^{\ast }$ 的 Kleene 闭包建索引。索引结构为 { a 1 , a 2 , ⋯   , a k } \{a_1, a_2, \cdots, a_k\} {a1​,a2​,⋯,ak​} 的诱导子图（induced subgraph ，即仅保留以集合元素为边标签的边及其端点的图）上的一种可达性索引，称为 FERRARI [7] 。获得诱导子图后在其上运行 FERRARI 的构建算法即可构建此索引。

针对其他类型正则表达式的索引包括：（均可对任意正则表达式建索引）

• [3] ：索引结构为有序表，每个条目形如 $⟨l,s,t⟩$ ，其中 $s$, $t$ 为路径的起始和目标结点，$l$ 为路径边上标签依次连接而成的字符串。索引构建算法即为：对每条长度至多为 $k$ （参数）的路径，将相应的 $⟨l,s,t⟩$ 保序地插入到表中。
• PAIRPQ [4] ：索引结构与 [3] 相同。区别在于索引构建算法中，首先通过贪心算法选出长度至多为 $k$ 的路径中较为频繁的（贪心思想体现在假设更长的频繁路径必由更短的频繁路径连接而成），再如 [3] 对这些频繁路径构建索引。
• MR-index [5] ：索引结构为经过 [2] 中边级别缩减的图，其邻接矩阵的压缩形式。（根据 $R$ 缩减的邻接矩阵中为 1 的元素对应的结点对在原图中通过满足 $R$ 的路径可达。）索引构建算法首先执行边级别缩减，然后对得到的图的邻接矩阵进行压缩。压缩方法称为 $K^2$ -树，针对稀疏 1-0 矩阵设计；其递归分割矩阵，每步将矩阵尽量等分为 $K^2$ 块，若一块中所有元素均为 0 ，则以树中的叶子结点表示，否则以内部结点表示，继续进行分割，分割出的小块矩阵在树中表示为其孩子结点。

查询计划

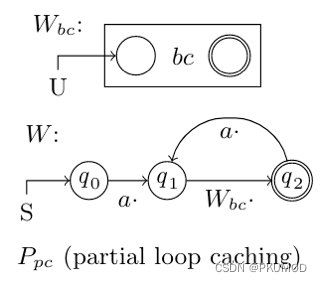
前人工作中主要有两类 RPQ 的查询计划：一类为基于有限自动机的计划，将查询中给定的正则表达式转换为确定性或非确定性有限自动机，以此指导图上的搜索；另一类为基于扩展关系代数的计划，在传统关系代数中加入表示传递闭包的运算符 $\alpha$ ，任意正则表达式即能转换为关系代数表达式树，自下而上执行。[9] 中提出了一种称为 Waveplan 的计划空间，其真包含以上的两类计划。例如下图 [9] 中的 $P_1$ 和 $P_2$ 即分别对应 $(ab{)}^{+}$ 基于有限自动机和扩展关系代数的计划：

同时，此计划空间中也存在前两类计划空间无法表达的计划，例如下述对应 $(abc{)}^{+}$ 的计划：

许多工作中提到了启发式的计划优化策略，如从图中较低频的边标签开始搜索 [9] [11-12] 、分割查询以对中间结果及时去重 [9] 等。

目前尚未有针对 RPQ 的查询计划代价估计和选择的统一框架。[9] 提出了一种代价模型，但没有给出代价估计的具体算法；[10] 给出了完整的代价模型和代价估计算法，但不能处理 Kleene 闭包。

总结

目前最前沿的 RPQ 相关工作主要关注索引构建和查询计划选择两方面，给出了多种对查询速度有实际提升效果的索引结构和相应的构建算法，并给出了统一的查询计划空间和启发式的计划优化策略；较为欠缺的方面包括没有统一考虑索引构建和查询计划选择、没有给出计划代价估计和选择的统一框架等。

参考文献

[1] X. Chen, Y. Peng, S. Wang, and J. X. Yu, “DLCR: efficient indexing for label-constrained reachability queries on large dynamic graphs,” Proc. VLDB Endow., vol. 15, no. 8, pp. 1645–1657, Apr. 2022.

[2] I. Na, I. Yi, K.-Y. Whang, Y.-S. Moon, and S. J. Hyun, “Regular Path Query Evaluation Sharing a Reduced Transitive Closure Based on Graph Reduction,” arXiv:2111.06918 [cs], Nov. 2021, Accessed: Dec. 20, 2021. [Online]. Available: http://arxiv.org/abs/2111.06918

[3] G. Fletcher, J. Peters, and A. Poulovassilis, “Efficient regular path query evaluation using path indexes.” OpenProceedings.org, 2016. doi: 10.5441/002/EDBT.2016.67.

[4] B. Liu, X. Wang, P. Liu, S. Li, and X. Wang, “PAIRPQ: An Efficient Path Index for Regular Path Queries on Knowledge Graphs,” in Web and Big Data, vol. 12859, L. H. U, M. Spaniol, Y. Sakurai, and J. Chen, Eds. Cham: Springer International Publishing, 2021, pp. 106–120. doi: 10.1007/978-3-030-85899-5_8.

[5] F. Tetzel, H. Voigt, M. Paradies, and W. Lehner, “An Analysis of the Feasibility of Graph Compression Techniques for Indexing Regular Path Queries,” in Proceedings of the Fifth International Workshop on Graph Data-management Experiences & Systems, Chicago IL USA, May 2017, pp. 1–6. doi: 10.1145/3078447.3078458.

[6] A. Gubichev, S. J. Bedathur, and S. Seufert, “Sparqling kleene: fast property paths in RDF-3X,” in First International Workshop on Graph Data Management Experiences and Systems, New York New York, Jun. 2013, pp. 1–7. doi: 10.1145/2484425.2484443.

[7] S. Seufert, A. Anand, S. Bedathur, and G. Weikum, “FERRARI: Flexible and efficient reachability range assignment for graph indexing,” in 2013 IEEE 29th International Conference on Data Engineering (ICDE), Brisbane, QLD, Apr. 2013, pp. 1009–1020. doi: 10.1109/ICDE.2013.6544893.

[8] Z. Abul-Basher, “Multiple-Query Optimization of Regular Path Queries,” in 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, Apr. 2017, pp. 1426–1430. doi: 10.1109/ICDE.2017.205.

[9] N. Yakovets, P. Godfrey, and J. Gryz, “Query Planning for Evaluating SPARQL Property Paths,” in Proceedings of the 2016 International Conference on Management of Data, San Francisco California USA, Jun. 2016, pp. 1875–1889. doi: 10.1145/2882903.2882944.

[10] V.-Q. Nguyen, Q.-T. Huynh, and K. Kim, “Estimating searching cost of regular path queries on large graphs by exploiting unit-subqueries,” J Heuristics, vol. 28, no. 2, pp. 149–169, Apr. 2022, doi: 10.1007/s10732-018-9402-0.

[11] A. Koschmieder and U. Leser, “Regular Path Queries on Large Graphs,” in Scientific and Statistical Database Management, vol. 7338, A. Ailamaki and S. Bowers, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012, pp. 177–194. doi: 10.1007/978-3-642-31235-9_12.

[12] D. Arroyuelo, A. Hogan, G. Navarro, and J. Rojas-Ledesma, “Time- and Space-Efficient Regular Path Queries on Graphs,” arXiv:2111.04556 [cs], Nov. 2021, Accessed: Dec. 26, 2021. [Online]. Available: http://arxiv.org/abs/2111.04556

[13] S. Afonin, “The View Selection Problem for Regular Path Queries,” in LATIN 2008: Theoretical Informatics, vol. 4957, E. S. Laber, C. Bornstein, L. T. Nogueira, and L. Faria, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2008, pp. 121–132. doi: 10.1007/978-3-540-78773-0_11.

[14] A. Skubella, D. Janke, and S. Staab, “BeSEPPI: Semantic-Based Benchmarking of Property Path Implementations,” in The Semantic Web, vol. 11503, P. Hitzler, M. Fernández, K. Janowicz, A. Zaveri, A. J. G. Gray, V. Lopez, A. Haller, and K. Hammar, Eds. Cham: Springer International Publishing, 2019, pp. 475–490.

[15] G. Bagan, A. Bonifati, R. Ciucanu, G. H. L. Fletcher, A. Lemay, and N. Advokaat, “gMark: Schema-Driven Generation of Graphs and Queries,” IEEE Trans. Knowl. Data Eng., vol. 29, no. 4, pp. 856–869, Apr. 2017, doi: 10.1109/TKDE.2016.2633993.

[16] Erling, Orri, et al. “The LDBC social network benchmark: Interactive workload.” Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data. 2015.