💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

文献来源：

@article{gu2022multi,
  title={Multi-level Adaptation for Automatic Landing with Engine Failure under Turbulent Weather},
  author={Gu, Haotian and Jafarnejadsani, Hamidreza},
  journal={arXiv preprint arXiv:2209.04132},
  year={2022}
}

运行MASC示例
1.打开定义引擎输出纬度、经度和高度的程序。然后首先把飞机放到发动机坏掉的地方。然后单击右上角的停止按钮×平面窗口的角落。
2在故障位置配置块中设置发动机输出全局位置

3.在simulink框架中设置机场坐标
4.单击运行按钮，首先启动模拟模型。
 

📚2 运行结果

 

 

 

 

部分代码：

tic
e = zeros(1,8000);
c = zeros(1,8000);
aileron_e = zeros(1,8000);
psi_ref = zeros(1,8000);
gamma_ref = zeros(1,8000);
%% This function is for testing for converge to planned straight line
xb = 31018;
yb = -23100;
xf = 34018;
yf = -27100;
Rl = 1016; % R value can not be small otherwise, the path following result is not good
psif = 0;
xl         =   xf + 4 * Rl * cos(psif - pi);
yl         =   yf + 4 * Rl * sin(psif - pi);
xu = xl + Rl * cos(psif - pi);
yu = yl + Rl * sin(psif - pi);
%Ru         =   sqrt((xl + Rl * cos(psif - pi) - xi)^2 + (yl + Rl * sin(psif - pi) - yi)^2);
%thetau     =   atan2( yi - yl - Rl * sin(psif - pi), xi - xl - Rl * cos(psif - pi));
%%
r = Rl; %radius of loiter curve
O = [xl yl]; %center of loiter or circular orbit
g = 9.81;%gravitational acceleration

%p = [curr_x curr_y];
p = [96900/3.2808 -84870/3.2808]; %UAV start position
psi = 4; %start heading
delta = 0.3; %look ahead position
%^^^^^^^^^^^^^^^^definition of controller parameters^^^^^^^^^^^^^^^^^^^^^^^
k_p=0.8;    %proportional gain
k_i=0.01;   %integral gain
k_d=1;      %derivative gain
%^^^^^^^^^^^^^^^^^^Specification of time step^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
dt=0.1  % this is a time unit which shoud match simulator x-plane
U_0=400; %initial UAV speed
U_d=435.9;%desired UAV speed
theta = atan2((p(2)-O(2)),(p(1)-O(1)));%Calculation of LOS angle
%^^^^^^^^^^^^^^^^^^^^^^^Definition of the look ahead point^^^^^^^^^^^^^^^^^
x_i = ((r*(cos(theta+delta)))+O(1));
y_i = ((r*(sin(theta+delta)))+O(2));
psi_d = atan2((y_i-p(2)),(x_i-p(1))); %commanded heading angle
u = (psi_d-psi); %controller input for changing heading angle
%^^^^^^^^^^^^^^^^^^^^^^^^^^^Motion of UAV^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
x_d=U_0*(cos(psi_d))*dt;
y_d=U_0*(sin(psi_d))*dt;
%^^^^^^^^^^^^^^^estimation of heading angle and position^^^^^^^^^^^^^^^^^^^
P_new = [(p(1)+x_d),(p(2)+y_d)];
psi_new = (psi+u);
%^^^^^^^^^^^^^^^^^^^^^over time positioning and heading of UAV^^^^^^^^^^^^^
X=[p(1)];
Y=[p(2)];
S=511; %area of  UAV wing
rho=0.3045; %density of air
b=59.64; %span of wing
mass = 333400  %mass of UAV 

I_xx=0.247e8; %inertial moment
L_p=-1.076e7; %rolling moment

Cl_da=0.668e-2;  %roll moment due to aileron deflection coefficient
Q_dS=1/2*rho*U_0^2*S; %dynamic pressure
L_da=Q_dS*b*Cl_da; %roll moment due to aileron
%^^^^^^^^^^^^^^^^^^^^^^^^^initialising controller^^^^^^^^^^^^^^^^^^^^^^^^^^
roll_ref=0; %initial UAV roll position
rollrate_ref=0; %initial UAV rollrate
t_ei=0; %thrust PI integrator
ei=0; %aileron PID integrator
%^^^^^^^^^^^^^^^^^^^estimation of stability derivatives^^^^^^^^^^^^^^^^^^^^
a=L_p/I_xx;
beta=L_da/I_xx;
roll_d=atan(u*U_0/g); %desired roll calculation
if abs(roll_d) > 1.5;
   if roll_d < 0;
      roll_d = -1.5;
   else if roll_d>0;
      roll_d = 1.5;
       end
   end
end
rollrate_d=roll_d*dt; %desired rollrate

aileron = k_p*(roll_d-roll_ref)+(k_i*ei)+k_d*(rollrate_d-rollrate_ref);
%deflection of aileron
rollrate_new = (((a*rollrate_ref)+(beta*aileron))*dt); %new roll rate output
roll_new = (rollrate_new/dt)+roll_ref; %new roll output
roll_old=roll_ref; %initialising old roll for feedback
rollrate_old=rollrate_ref; %initiallising old rollrate for feedback
%^^^^^^^^^^^^^^^^^^^^^^^^^control of thurst^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
t_ei=t_ei+(U_d-U_0)*dt;
thrust=k_p*(U_d-U_0)+(k_i*t_ei);
V_new=U_0+(thrust*dt);
V_old=V_new;
count = 0
while count<1000
Ru = abs ((((P_new(1) - O(1))^2) + ((P_new(2) - O(2))^2)) ^(1/2)-r);
%Calculation of UAV distance from center
theta_new = atan2((P_new(2)-O(2)),(P_new(1)-O(1))); %new path angle calculation

x_i = ((r*(cos(theta_new+delta)))+O(1));
y_i = ((r*(sin(theta_new+delta)))+O(2));
psi_d = atan2((y_i-P_new(2)),(x_i-P_new(1)));%calculation of desired heading angle
u = wrapToPi(psi_d-psi_new); %controller input for changing heading angle
ei=ei+((roll_d-roll_old)*dt); %updating the integrator
roll_d=atan(u*V_old/g); %desired roll calculation
if abs(roll_d) > 1.5; %limit of roll
    if roll_d < 0;
       roll_d = -1.5;
    else if roll_d>0;
       roll_d = 1.5;
        end
    end
end
rollrate_d=(roll_d-roll_old)*dt; %calculation of desired rollrate
aileron = (k_p*(roll_d-roll_old)+(k_i*ei)+(k_d*(rollrate_d-rollrate_old))); %calculation of deflection of aileron
rollrate_new = (((a*rollrate_old)+(beta*aileron))*dt); %new rollrate calculation

roll_new = (rollrate_new/dt)+roll_old; %new roll angle calculation
rollrate_old=rollrate_new; %rollrate as feedback

roll_old=roll_new; %roll angle as feedback
 
psi_old = psi_new; %UAV heading as feedback

psi_b=g/V_old*(tan(roll_new));
%due to new roll change in heading
psi_new = wrapToPi(psi_new+psi_b); %calculation of new heading angle
gamma_new = -15*pi/180;
Q_dS=1/2*rho*V_old^2*S; %calculation of dynamic pressure
L_da=Q_dS*b*Cl_da;
%due to aileron calculation of roll moment
beta=L_da/I_xx;
a=L_p/I_xx;
%^^^^^^^^^^^^^^^^^^^^^Calculation of UAV movements^^^^^^^^^^^^^^^^^^^^^^^^^
x_d=V_old*(cos(psi_new))*dt;
y_d=V_old*(sin(psi_new))*dt;
P_new = [(P_new(1)+x_d) (P_new(2)+y_d)];
%^^^^^^^^^^^^^^^^^^^^^^^^^contorl of thrust^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
t_ei=t_ei+(U_d-V_old)*dt;
thrust=k_p*(U_d-V_old)+(k_i*t_ei);
V_new=V_old+(thrust*dt);
V_old=V_new;
figure(1)
Y=[ Y P_new(2)];
X=[ X P_new(1)];
plot(X,Y)
hold on
Q = 0 : 0.01 : 2*pi;
W_c = (r * (cos(Q)))+O(1);
A_c = (r * (sin(Q)))+O(2);
plot(W_c,A_c,':')

xlim([xl-2*Rl xl+2*Rl])
ylim([yl-2*Rl yl+2*Rl])
xlabel('x-direction in ft')
ylabel('y-direction in ft')
title('Followed path using carrot chasing algorithm')
drawnow
count = count+1
hold on
for j = count;
%array of measurements
d = (abs(((O(1)-P_new(1))^2)+((O(2)-P_new(2))^2))^(1/2)) ;
e(1,j) = u;
c(1,j) = Ru;
aileron_e(1,j) = aileron;
if psi_d >=0
    psi_ref(1,j) = psi_d;
elseif psi_new < 0
    psi_ref(1,j) = psi_d+2*pi;
end
%psi_ref(1,j) = psi_new;
DesiredHeading = psi_ref(1,j);
disp(DesiredHeading)
gamma_ref(1,j) = gamma_new;
DesiredFlightPath = gamma_ref(1,j);
disp(DesiredFlightPath)
end
hold off
end
toc
%^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^measurment plots^^^^^^^^^^^^^^^^^^^^^^^^^^^^
figure(2)
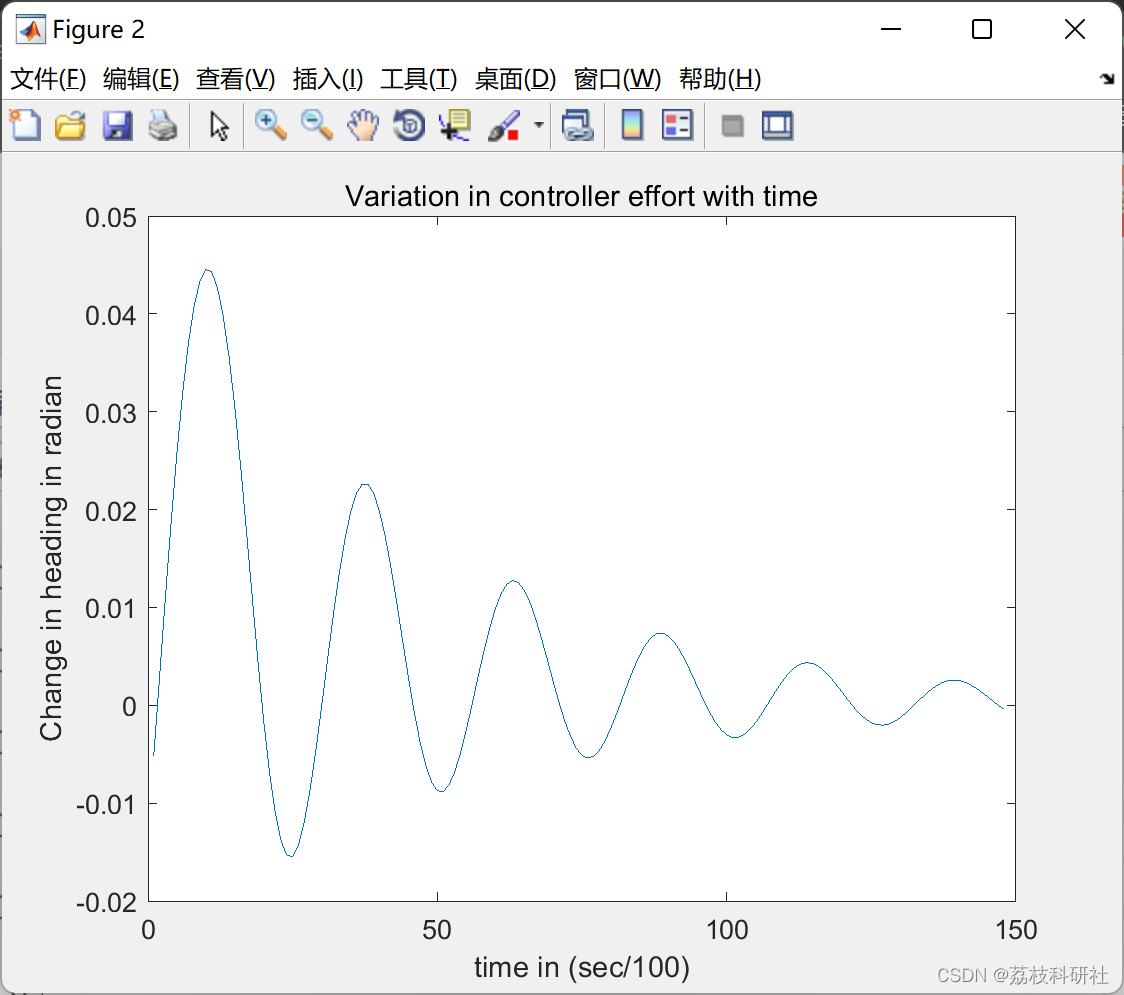
f = [1:1:count];
plot(f,e)
xlabel('time in (sec/100)')
ylabel('Change in heading in radian')
title('Variation in controller effort with time')
figure(3)
plot(f,c)
xlabel('time in (sec/100)')
ylabel('cross track deviation(ft)')
title('Variation of cross track deviation with time')
figure(4)
plot(f,aileron_e)
xlabel('time in (sec/100)')
ylabel('Deflection of aileron in radian')
title('Variation in aileron control with time')
figure(5)
plot(f,psi_ref)
xlabel('time in (sec/100)')
ylabel('heading new in radian')
title('Variation in controller effort with time')
figure(6)
plot(f,gamma_ref)
xlabel('time in (sec/100)')
ylabel('pitch angle in radian')
title('Variation in controller effort with time')
time=count*dt

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

@article{gu2022multi,
  title={Multi-level Adaptation for Automatic Landing with Engine Failure under Turbulent Weather},
  author={Gu, Haotian and Jafarnejadsani, Hamidreza},
  journal={arXiv preprint arXiv:2209.04132},
  year={2022}
}

🌈4 Matlab代码实现