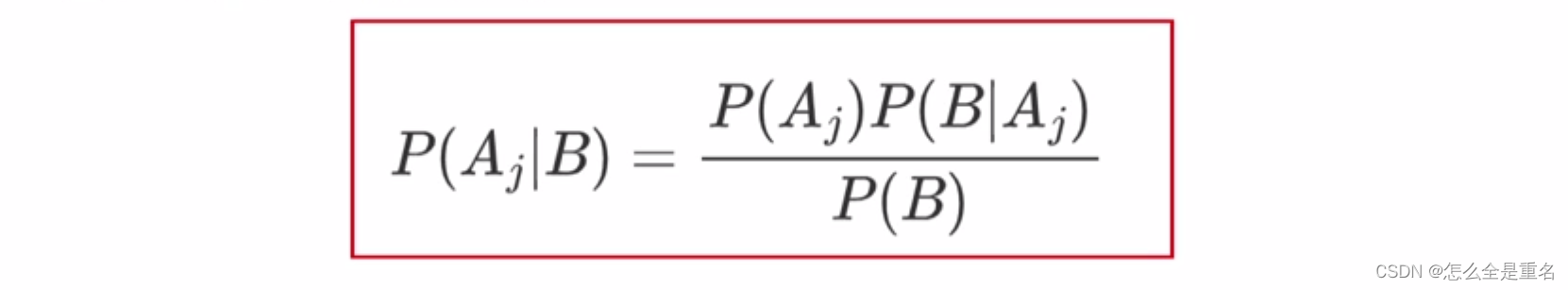
释义

贝叶斯定理是“由果溯因”的推断，所以计算的是"后验概率"
其中：
P(A|B) 表示在事件 B 已经发生的条件下，事件 A 发生的概率。
P(B|A) 表示在事件 A 已经发生的条件下，事件 B 发生的概率。
P(A) 和 P(B) 分别表示事件 A 和事件 B 单独发生的概率

简单代码实例

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 文本数据集
documents = [
    "这是一个正面文本。",
    "这是一个负面文本。",
    "这是一个正面文本。",
    "这是一个负面文本。",
    "这是一个正面文本。"
]

# 对应的标签
labels = [1, 0, 1, 0, 1]

# 将文本转换为词袋表示
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(documents)

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, labels, test_size=0.2, random_state=42)

# 创建朴素贝叶斯分类器
clf = MultinomialNB()

# 训练分类器
clf.fit(X_train, y_train)

# 使用分类器进行预测
y_pred = clf.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("准确率:", accuracy)