---

引言

以前学概率论的时候，不知道后面的数理统计是什么，所以简称都把后面的省略掉了。现在接触的学科知识多了，慢慢就对数理统计有了直观印象。

尤其是第一次参加数模比赛的时候，各种统计方法，不知如何下手。不过利用像 Spss 这样的软件，只要把数据导进来，点点就能实现复杂统计处理。但是我还是心里发虚，因为不知道如何解释这些软件统计出来的结果。看着出来的各种 p 值，Sig. 等等，只会照猫画虎学网上说怎么怎么样。

扯远了，不过对这一章我还是很有学习欲望的，希望能顺利掌握考试所需要的知识点，同时也为以后打下一个统计学基础。

---

一、基本概念

1.1 总体

我们经常需要研究某类特定对象的某一特征，如全国的粮食产量、青少年的身高、体重等指标。所研究对象的某项指标的全体称为总体，记为 $X$ ，其中构成总体的每个元素称为个体。

从本质上来说，总体即一个随机变量。

1.2 样本

对于总体数量太多，如全国商品的价格波动、某个企业生产的所有照明灯的寿命，对每个个体进行研究会花费大量人力物力，所以我们往往只研究一定数量的具有代表性的个体的特征，来大致反映总体的特征。

从总体中随机抽取若干个个体构成的几何，称为总体的一个样本。

设总体为 $X$ ，从总体 $X$ 中取出含 $n$ 个个体的样本（$X_1,X_2,\cdots ,X_n$），$n$ 称为样本的容量，若样本（$X_1,X_2,\cdots ,X_n$）满足：

1. $X_1,X_2,\cdots ,X_n$相互独立；
2. 样本 $X_1,X_2,\cdots ,X_n$ 中每个个体与总体 $X$ 分布相同，

称（$X_1,X_2,\cdots ,X_n$）为来自总体 $X$ 的简单随机样本。设 $x_1,x_2,\cdots ,x_n$ 为样本的一组抽样取值，称其为样本（$X_1,X_2,\cdots ,X_n$）的一组观察值。

1.3 统计量

设 $X$ 为总体，（$X_1,X_2,\cdots ,X_n$）为来自总体 $X$ 的简单随机样本，以样本（$X_1,X_2,\cdots ,X_n$）为变量所构造的不含任何参数的函数称为统计量。其本质是随机变量。

如 $(X_1+X_2)/2,X_1^2+X_2^2+X_3^2$ 等等都不含参数，故都是统计量；以下为一些常见的统计量：

1. 样本均值 $$\overline{X}=\frac{1}{n}\sum _{i=1}^n{X}_i;$$
2. 样本的 $k(k=1,2,\cdots )$ 阶原点矩 $$A_k=\frac{1}{n}\sum _{i=1}^n{X}_i^k;$$
3. 样本的 $k(k=1,2,\cdots )$ 阶中心矩 $$B_k=\frac{1}{n}\sum _{i=1}^n(X_i-\overline{X}{)}^k;$$
4. 样本方差 $$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\overline{X}{)}^2=\frac{1}{n-1}{B}_2,$$ 其中 $S$ 称为样本均方差。

设 $X$ 为总体，且 $(X_1,X_2,\cdots ,X_n)$ 为来自总体 $X$ 的简单随机样本，且 $E(X)=\mu ,D(X)={\sigma }^2$ ，则 $$E(\overline{X})=\mu ,D(\overline{X})=\frac{{\sigma }^2}{n},E(S^2)={\sigma }^2.$$ 咱可以简单证明一下。

对 $E(\overline{X})=\mu$ ，即样本均值的期望为总体的期望，证明如下：$$E(\overline{X})=\frac{1}{n}\sum _{i=1}^{n}E(X_i)=\frac{n\mu }{n}=\mu .$$ 主要是利用了独立变量 $E(X_1+X_2+\cdots +X_n)=E(X_1)+\cdots +E(X_n)$ 。

对 $D(\overline{X})=\frac{{\sigma }^2}{n}$ ，即样本均值的方差为总体方差的均值，证明如下：$$D(\overline{X})=D(\frac{1}{n}(X_1+X_2+\cdots +X_n))=\frac{1}{n^2}\sum _{i=1}^{n}D(X_i)=\frac{n{\sigma }^2}{n^2}=\frac{{\sigma }^2}{n}.$$ 同样也只是利用独立变量方差加和的性质。

对 $E(S^2)={\sigma }^2$ ，即样本方差的期望为总体的方差，证明如下：

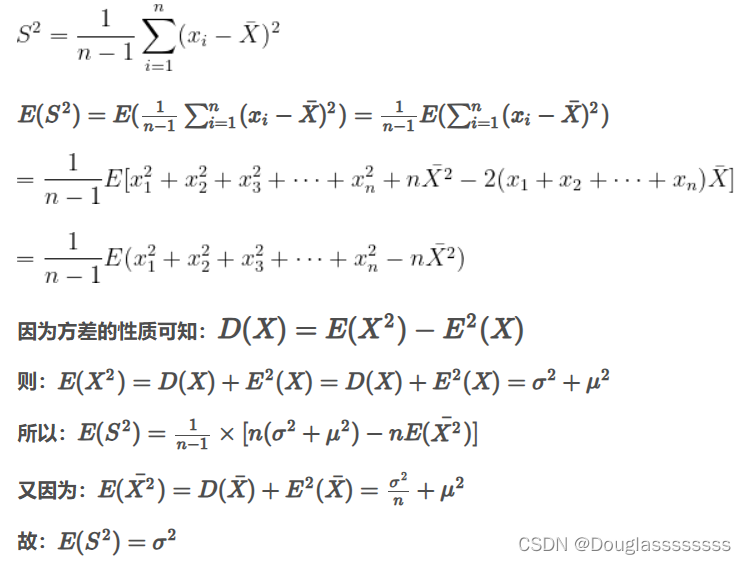
1.4 顺序统计量

设 $X$ 为总体，且 $(X_1,X_2,\cdots ,X_n)$ 为来自总体 $X$ 的简单随机样本，将 $(X_1,X_2,\cdots ,X_n)$ 按照样本观察值大小进行排序，称为顺序统计量。

称 $\min (X_1,X_2,\cdots ,X_n)$ 为最小统计量，$\max (X_1,X_2,\cdots ,X_n)$ 为最大顺序统计量。

---

写在最后

基本概念就到这里，下一篇我们来看看三个重要的抽样分布。