最近在用JavaScript刷动态规划的题组,刷了一半感觉只刷题不写笔记的话印象没那么深刻,所以从今天开始来记录一下刷题情况。
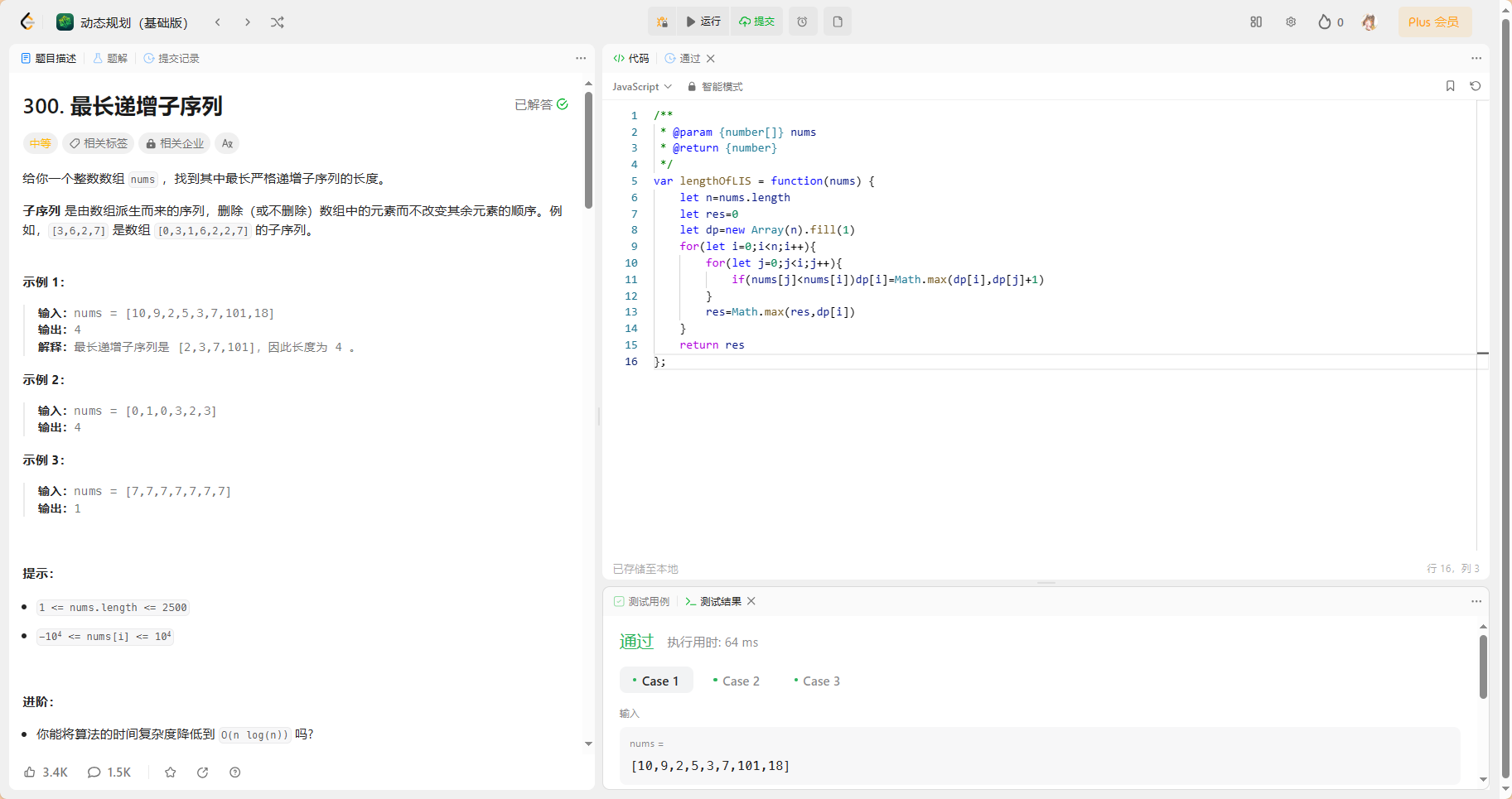
力扣T300 300. 最长递增子序列
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。
这道题的思路是:
判断以第i个元素为结尾的最长子序列的长度
dp【i】的含义是以第i个元素为结尾的最长子序列的长度
在动态规划过程中,我们依次遍历每个元素,在遍历当前元素时,让该元素与之之前的每个元素大小作比较,如果nums【i】元素大于nums【j】元素,说明nums【i】可以在已经以nums【j】为结尾的最长子序列基础上接上去构成+1大小的最长子序列。并且在内循环遍历过程中要不断和自身dp【i】做比较看是否需要更新最长子序列长度。
遍历完一个元素的情况之后要更新当前获取的最长子序列长度
/**
* @param {number[]} nums
* @return {number}
*/
var lengthOfLIS = function(nums) {
let n=nums.length
let res=0
let dp=new Array(n).fill(1)
for(let i=0;i<n;i++){
for(let j=0;j<i;j++){
if(nums[j]<nums[i])dp[i]=Math.max(dp[i],dp[j]+1)
}
res=Math.max(res,dp[i])
}
return res//更新当前获取的最长子序列长度
};在此题的基础上,变化一下要求,要求获得的不是最长递增子序列的长度,而是该长度的子序列的个数,就变成了下面这道题:
力扣T673 l673. 最长递增子序列的个数
给定一个未排序的整数数组
nums, 返回最长递增子序列的个数 。注意 这个数列必须是 严格 递增的。
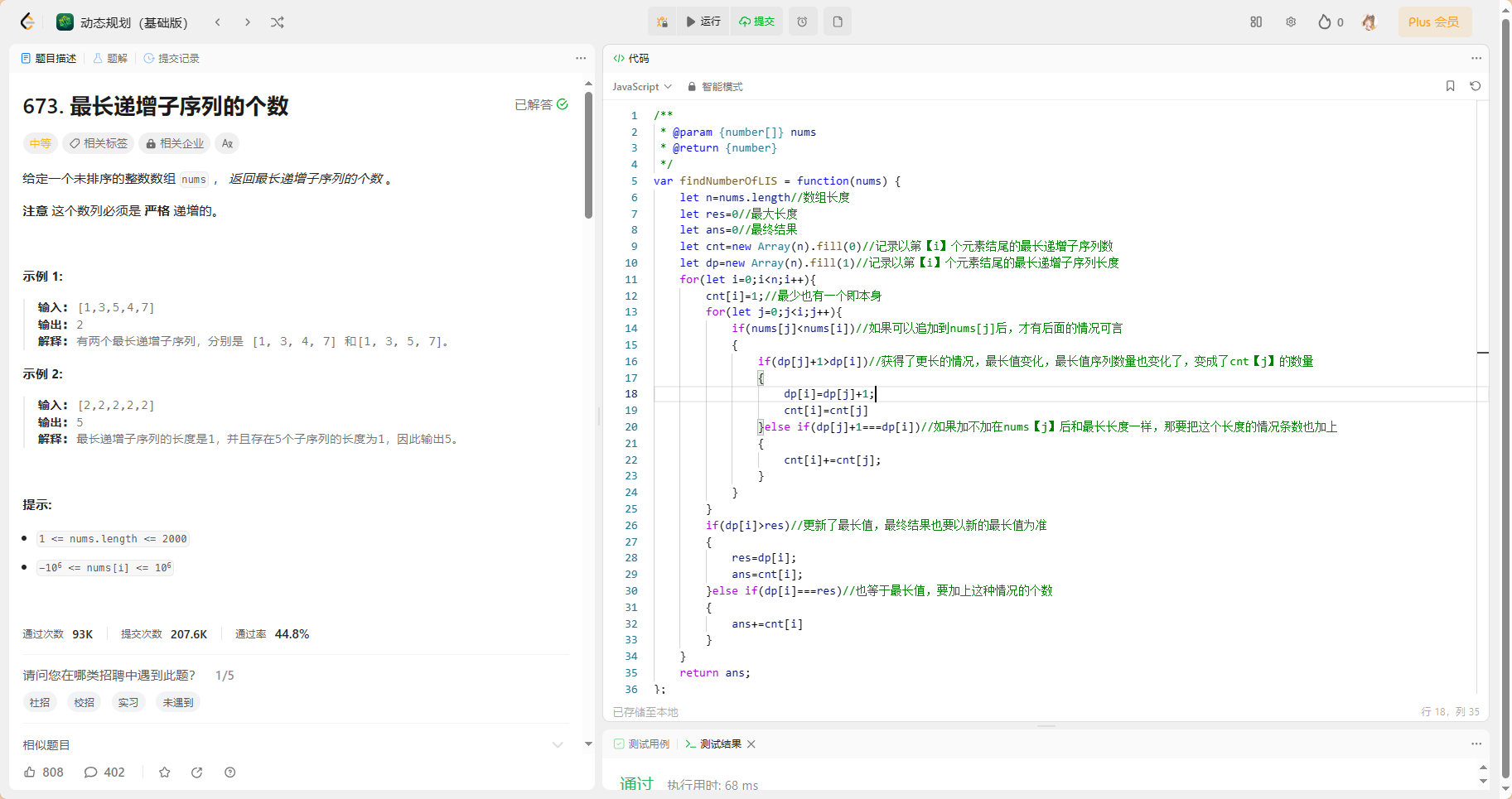
在上一题的基础上,这题需要增加一个记录以每个元素为结尾的最长子序列的个数数组cnt
在每轮遍历更新最大值时,要随后更新对应的个数。
注意初始化数组dp和cnt时需要赋初值为1
因为对于每个元素本身,dp【i】和cnt【i】最少为1
相对上一道题,这里需要考虑更新最大值时,dp【i】=dp【j】+1的情况
如果dp【i】<dp【j】+1,可以放心大胆的换新的dp和cnt
但 如果等于时,相当于不影响最长值但有同样长度效果的另一种情况,所以要加上这种情况的个数
在每次遍历完当前元素更新最大值时,也需要进行这样的判断才不会漏掉情况。
/**
* @param {number[]} nums
* @return {number}
*/
var findNumberOfLIS = function(nums) {
let n=nums.length//数组长度
let res=0//最大长度
let ans=0//最终结果
let cnt=new Array(n).fill(1)//记录以第【i】个元素结尾的最长递增子序列数
let dp=new Array(n).fill(1)//记录以第【i】个元素结尾的最长递增子序列长度
for(let i=0;i<n;i++){
for(let j=0;j<i;j++){
if(nums[j]<nums[i])//如果可以追加到nums[j]后,才有后面的情况可言
{
if(dp[j]+1>dp[i])//获得了更长的情况,最长值变化,最长值序列数量也变化了,变成了cnt【j】的数量
{
dp[i]=dp[j]+1;
cnt[i]=cnt[j]
}else if(dp[j]+1===dp[i])//如果加不加在nums【j】后和最长长度一样,那要把这个长度的情况条数也加上
{
cnt[i]+=cnt[j];
}
}
}
if(dp[i]>res)//更新了最长值,最终结果也要以新的最长值为准
{
res=dp[i];
ans=cnt[i];
}else if(dp[i]===res)//也等于最长值,要加上这种情况的个数
{
ans+=cnt[i]
}
}
return ans;
};