损失函数

• 损失函数$L(y_i,{\hat{y}}_i)$用来描述神经网络的输出${\hat{y}}_i$和基本事实（Ground Truth，GT）$y_i$的差异
• 对于回归问题，常用均方误差（Mean Square Error，MSE）损失函数
  $$L(y_i,{\hat{y}}_i)={\Vert y_i-{\hat{y}}_i\Vert }_2^2$$
• 神经网络的训练过程就是寻找一组参数$\theta$，使得神经网络在一个batch的训练上，损失函数的和最小
  $$\theta =\arg \underset{\theta }{\min }\sum _{i=1}^{N}L(y_i,{\hat{y}}_i)$$
• 对于说话人识别，通常有两种类型的损失函数
  • 将说话人识别看作一个多说话人分类问题，即模拟说话人辨认问题
  • 将说话人识别看作一个二值决策问题，即模拟说话人验证问题

多说话人分类

• 在该问题中，假设不同的说话人属于不同的类
• 训练时
  • 每个说话人都有一个全局唯一标签
  • 每个话语（Utterance）都有一个说话人标签
• 运行时
  • 需要识别在训练集中未出现过的说话人，因此无法使用训练数据的标签作为输出
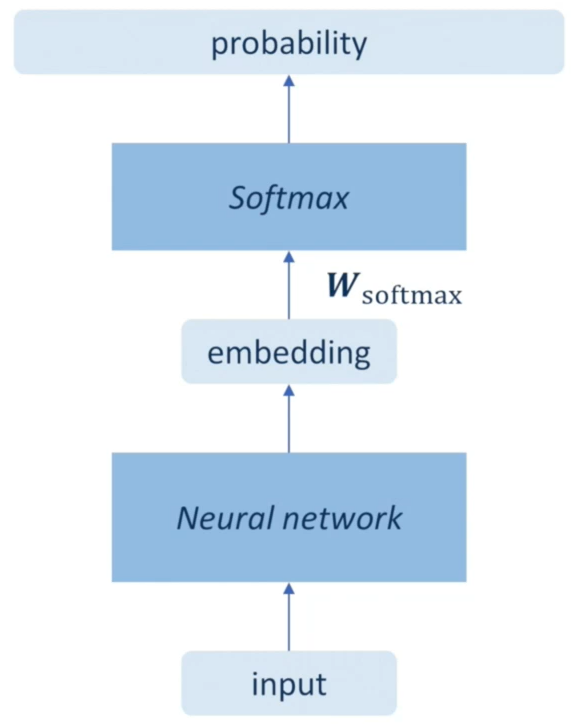
• 得到嵌入码之后，需要经过一个MLP（该MLP的激活函数是Softmax），得到该嵌入码属于训练数据中哪一个说话人的概率分布
  

Cross Entropy Loss

• 得到概率分布后，使用交叉熵（Cross Entropy，CE）损失函数，计算预测的概率分布，与真实的概率分布之间的差距，假设概率分布的向量维度为K
  $$H(p,q)=-\sum _{i=1}^K{p}_i\cdot \ln q_i$$
  其中，
  • $p$是真实的概率分布，采用独热向量（One-hot Vector），即只有真实说话人对应的值为1，其他的值都为0
  • $q$是预测的概率分布，经过Softmax激活函数之后，最大值接近1，所有值求和等于1
  • 由于$p$为独热向量，所以损失函数简化为$H(p,q)=-\ln q_j$，$q_j$指预测的概率分布中，真实说话人对应的概率
  • $H(p,q)$的值越小，代表两个分布越接近
• 训练时：在训练数据上，最小化$H(p,q)$来优化参数
• 运行时：直接使用嵌入码，用于说话人识别（可用余弦相似度、欧氏距离等）
• 这种方法的缺点
  • 用于计算概率分布的MLP，其参数会随着训练数据说话人数量线性增加
  • 例如嵌入码的维度是1280，训练数据有1000人，那么MLP的参数矩阵$W_{Softmax}\in R^{1000\times 1280}$，光是MLP的参数量就达到了128万
  • 训练集中，部分说话人的数据量较少，这意味着$W_{Softmax}$中，有部分参数极少发挥作用，但是前向传播时每次都需要计算整个矩阵，这导致训练过程中，花费了大量的资源用于优化几乎没有用的参数
  • $W_{Softmax}$只在训练时发挥作用，与运行时的相似度计算不完全一致，这会导致网络难以泛化到训练集中未出现过的说话人

Angular Softmax

• 为了改善训练和运行时，目标不匹配的问题，Softmax有一个变种，叫做Angular Softmax，思路如下：
  1. 将$W_{Softmax}$中的每个行向量$w_r$都限制为单位长度的向量，设嵌入码为$e$，那么$w_r\cdot e=||e||\cos {\theta }_i$
  2. $W_{Softmax}\cdot e$的运算结果，就是$e$的范数，乘以一个余弦值，此时的优化过程，会与运行时的相似度计算更加一致
• 注意，关于Softmax的计算，如果幂的值很大，取指数会导致溢出（即便是Python也要考虑这个问题），此时需要令输入向量中的每一个值，都减去向量中的最大值，然后再进行标准的Softmax运算，这不影响运算结果，但是保证了数值计算的稳定，原因如下
  $$\begin{array}{rl}{y}_i& =\frac{exp(x_i-x_{max})}{{\sum }_{j=i}^{K}exp(x_j-x_{max})}\\ & =\frac{exp(x_i)/exp(x_{max})}{{\sum }_{j=i}^K[exp(x_j)/exp(x_{max})]}\\ & =\frac{exp(x_i)}{{\sum }_{j=i}^{K}exp(x_j)}\end{array}$$

二值决策

• 针对多说话人分类方法，训练和运行时，目标不匹配的问题，研究人员提出二值决策方法
• 给定两个话语，网络对这两个话语进行二值决策：
  • 0，表示两个话语来自不同的说话人
  • 1，表示两个话语来自同一个说话人
• 损失函数必须基于，由至少两个话语组成的样本，来定义

Pairwise Loss

• 假设有两个输入$x_i$和$x_j$，它们都进入同一个网络，得到两个嵌入码，两个嵌入码的余弦相似度是$s_{ij}$，假设GT表示为：
  $$y_{ij}=\{\begin{array}{c}0,若x_i和x_j来自不同的说话人\\ 1,若x_i和x_j来自同一个说话人\end{array}$$
• 对应的损失函数为$L(s_{ij},y_{ij})$
• 可以将这个问题视为二分类问题，使用二元交叉熵（Binary Cross Entropy，BCE）损失函数
  $$L_{BCE}(s,y)=-y\ln s-(1-y)\ln (1-s)$$
• 由于要对余弦相似度取对数，而余弦相似度可能为负数，所需需要将$s$变换为正数，常见做法：
  $$s^{\prime }=\sigma (ws+b)=\frac{1}{1+exp(-(ws+b))}$$
  其中，$w$和$b$都是可学习参数，$w>0$，$\sigma (\cdot )$是Sigmoid函数。从而，损失函数变为$L_{BCE}(s^{\prime },y)$，这就是基于样本对的损失函数Pairwise Loss
• 缺点：由于网络参数随训练过程变化，所以难以平衡正样本和负样本在训练过程中的数量平衡

Triplet Loss

• 针对Pairwise Loss的缺点，研究人员提出了基于三元组的损失函数Triplet Loss
• 先思考：在设计损失函数时，我们希望给网络的监督信息的效果是什么？
  • 对于同一个说话人的嵌入码，我们希望这两个嵌入码在嵌入码空间中越接近越好
  • 对于不同的说话人的嵌入码，我们希望这两个嵌入码在嵌入码空间中越远离越好
• 针对上述思考，Triplet Loss需要挑选三个话语：
  1. 锚样本（Anchor）$x^a$
  2. 正样本（Positive）$x^p$，和锚样本来自同一个说话人
  3. 负样本（Negative）$x^n$，和锚样本来自不同的说话人
• 那么，这三个话语的嵌入码，经过参数更新后效果如下图所示：
  
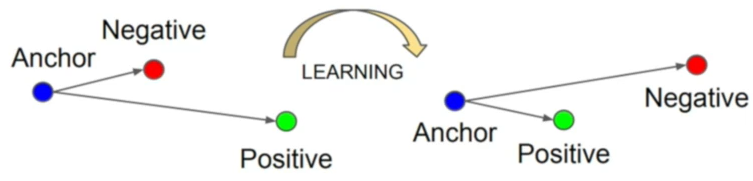
• 数学形式
  $$L=[{\Vert f(x^a)-f(x^p)\Vert }_2^2-{\Vert f(x^a)-f(x^n)\Vert }_2^2+\alpha {]}_{+}$$
  其中，
  • $f(x)$表示$x$的嵌入码
  • $\alpha \ge 0$，是预先定义的超参数，表示正样本，相对于负样本，更靠近锚样本的距离
  • $[x{]}_{+}$表示函数$max(x,0)$
  • ${\Vert \Vert }_2^2$表示欧氏距离的平方
• 上述形式的Triplet Loss常用于人脸识别，对于说话人识别，会将欧氏距离改为余弦相似度：
  $$L=[\cos (f(x^a),f(x^n))-\cos (f(x^a),f(x^p))+\alpha {]}_{+}$$
  
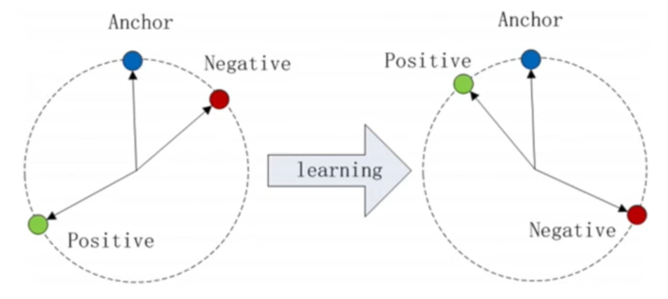
• 注意，由于欧氏距离是越小越靠近，而余弦相似度是越大越靠近，所以对比上一个式子，正样本对之间的距离，和负样本对之间的距离，要交换位置
• 关键点
  • 正样本对和负样本对的选择，对于训练的效率非常关键
  • 需要挖掘困难样本，至少使$[x{]}_{+}$是正数，否则不会有梯度信息
  • 由于网络参数随训练过程变化，所以难以提前找到困难样本
  • 困难样本挖掘的办法：
    • 离线挖掘：每训练一定的步数，根据当前的网络参数，计算训练集的嵌入码，根据此时的嵌入码选取困难样本
    • 在线挖掘：对每个batch，计算里面每个样本的嵌入码，构造一个最困难的样本

端到端的说话人识别系统

• 对于端到端的定义，业界尚无明确定论，一般而言：
  • 第一个“端”，是指系统的输入，如音频数据
  • 第一个“端”，是指系统的输出，如预测结果
• 端到端系统应满足下列条件：
  • 除了神经网络外，不再使用任何其他模型，不能有GMM、因子分析、PLDA等
  • 采用单一的一个神经网络进行推理
  • 采用一个损失函数进行参数优化
• 端到端的损失函数，能够在训练时，完全模拟运行时的情况。说话人识别在运行时的特点：
  • 注册阶段，有多个注册话语，需要对这些话语提取嵌入码，然后聚合
  • 识别阶段，话语可能来自真实说话人或仿冒说话人，需要给出二值决策

端到端的损失函数

• 在训练时，使用$N+1$个话语
  • 其中$N$个话语来自真实说话人
  • 另外一个话语来自真实说话人或仿冒说话人
• 这$N+1$个话语，经过同一个神经网络，其中来自真实说话人的$N$个话语的嵌入码，被聚合（通常是取平均），成为说话人模型
• 另外一个嵌入码，与说话人模型计算余弦相似度
• 余弦相似度经过变换成为正数，然后计算二元交叉熵损失
  $$\begin{array}{rl}{s}^{\prime }& =\sigma (ws+b)=\frac{1}{1+exp(-(ws+b))}\\ L_{BCE}(s^{\prime },y)& =-y\ln s^{\prime }-(1-y)\ln (1-s^{\prime })\end{array}$$
  
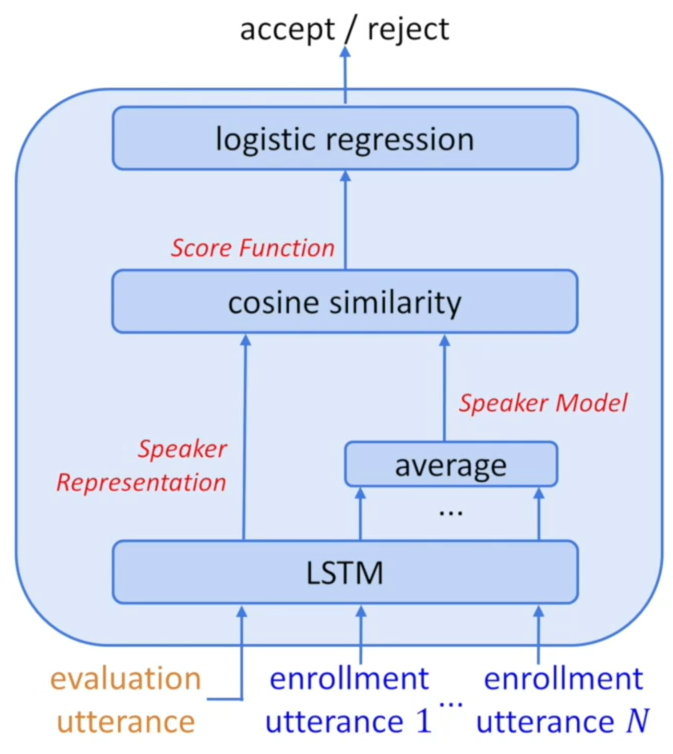
• 最后的损失函数计算过程，非常类似Pairwise Loss，只不过端到端系统的输入是$N+1$个话语，而不是两个话语
• x-vector系统采用的是类似上述的端到端损失函数，不过将余弦相似度，替换成了另一种相似性度量：
  $$L(e_1,e_2)=e_1^T{e}_2-e_1^{T}S{e}_1-e_2^{T}S{e}_2+b$$
  其中，
  • 矩阵$S$和标量$b$都是可学习参数
  • 这是基于PLDA所衍生出来的一种相似性度量
• 关键点
  • 关于$N$的选定，可以按照运行时的情况来决定，如果不确定运行时会有几个注册话语，则取平均值或者中间值
  • 如何平衡正负样本比例？这是常见的问题，通常负样本数远远多于正样本数，常见的做法是：在负样本的损失函数上，乘以一个常数$K，0<K<1$

广义端到端损失函数（Generalized End-to-End Loss，GE2E）

• 基本思想
  • 通过减少一个batch中的重复计算，使训练更加高效
  • 对于一个batch中的所有负样本而言，只关注最困难的那个样本，利用最大间隔原理（梦回SVM）
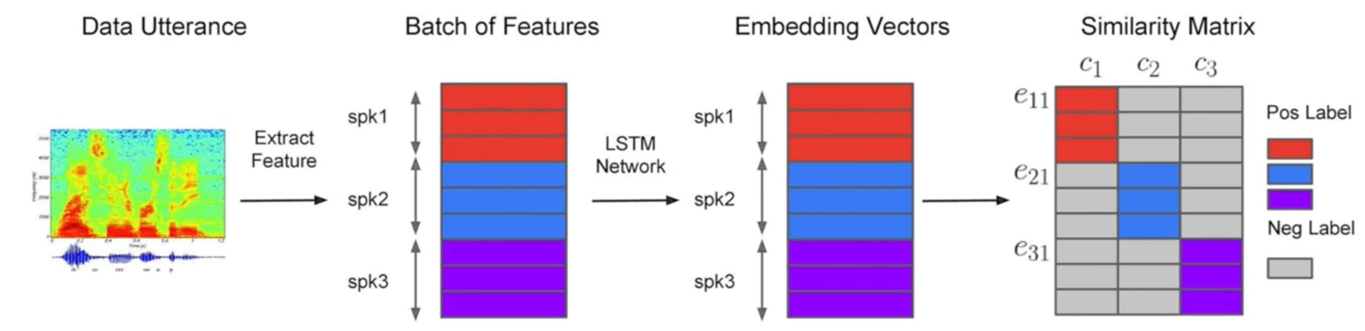
• 接下来将视角放在一个batch的数据中：
  
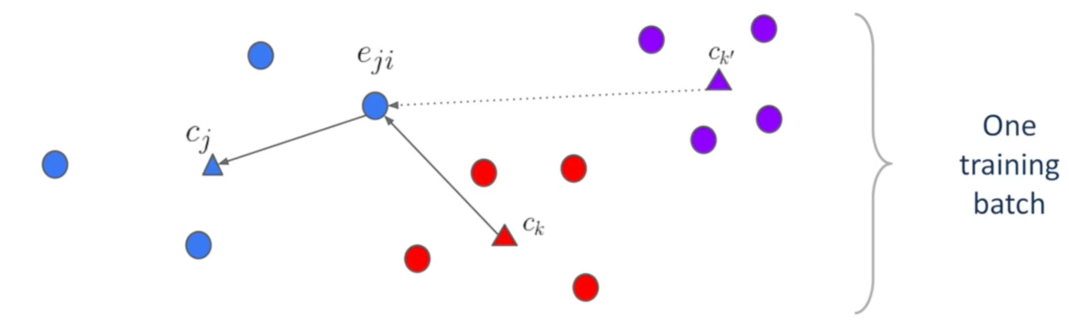
• 上图中，每个圆圈是一个话语的嵌入码，不同的颜色表示该话语来自不同的说话人。可见上图中有三个说话人，每个说话人对应四个嵌入码
• 用正三角形表示每个说话人的嵌入码的中心点（也叫质心，论文中叫Centroid）
• 将嵌入码记为$e_{ji}$，$j$表示说话人，$i$表示属于第$j$个说话人的第$i$个话语；某个说话人的嵌入码中心记为$c_j$
• 基本思想，具体而言：
  • 对于每一个$e_{ji}$而言，我们希望它与$c_j$靠近，与其他的$c_k、c_{k^{\prime }}$远离
  • 在一个batch内，对于一个$e_{ji}$而言，会出现多个其他说话人的中心点，如$c_k、c_{k^{\prime }}$
  • 根据最大间隔原理，只关注距离该$e_{ji}$最接近的其他说话人的中心，从图中来看，则是只关注$c_k$，不关注$c_{k^{\prime }}$
  • 对神经网络而言，$c_k$是区分$e_{ji}$属于$c_j$，最困难的一个其他说话人。也就是说，对于$e_{ji}$而言，$c_k$是支持说话人（Support Speaker）
• 计算损失函数前的准备工作
  • 假设，一个batch的维度为$N\times M$，$N$表示该batch包含的说话人个数，$M$表示该batch中每个说话人的话语数
  • 该batch的数据，经过神经网络后，每个话语都向量化，得到嵌入码$e_{ji}$，从而：
    $$c_j=\frac{1}{M}\sum _{i=1}^M{e}_{ji}$$
  • 对整个batch，计算相似度矩阵，维度为$NM\times N$：
    $$S_{ji,k}=w\cdot \cos (e_{ji},c_k)+b$$
    其中，
    • $w>0，w、b$都是可学习参数
    • 相似度矩阵，表示batch中的每一个嵌入码$e_{ji}$，与batch内所有说话人的中心点$c_k$，计算相似度，然后进行线性变换，因此维度是$NM\times N$
• 损失函数的定义：有两种方法实现最大间隔原理

1. 基于对比的方法：对于每一个$e_{ji}$而言，损失函数为
   $$L(e_{ji})=1-\sigma (S_{ji,j})+\underset{1\le k\le N,k\ne j}{\max }\sigma (S_{ji,k})$$
   其中，
   • $1-\sigma (S_{ji,j})$表示正样本对的余弦相似度越接近1越好
   • ${\max }_{1\le k\le N,k\ne j}\sigma (S_{ji,k})$表示最困难负样本对的余弦相似度越小越好
   • 这种同时考虑正样本对和负样本对的思想，与Triplet Loss类似，不同之处在于：
     • 使用中心点，模拟运行时的说话人嵌入码
     • 负样本对的优化，只针对支持说话人
   • 缺点：使用了$\max (\cdot )$，这是不可导的函数
2. 基于Softmax的方法，针对方法1的缺点，采用$\max (\cdot )$的可微分版本——Softmax来改进
   $$\begin{array}{rl}L(e_{ji})& =-S_{ji,j}+\ln \sum _{k=1}^N\exp (S_{ji,k})\\ & =-\ln (\exp (S_{ji,j}))+\ln \sum _{k=1}^N\exp (S_{ji,k})\\ & =\ln \frac{{\sum }_{k=1}^N\exp (S_{ji,k})}{\exp (S_{ji,j})}\\ & =-\ln \frac{\exp (S_{ji,j})}{{\sum }_{k=1}^N\exp (S_{ji,k})}\end{array}$$
   这个损失函数，将每个嵌入码推到其对应说话人中心点附近，并将其拉离所有其他说话人中心点

• 关键点
  • 神经网络在优化时，会收敛到一个平凡解（Trivial Solutions），类似于微分方程的特解，会导致所有嵌入码都变成相同的值
  • 为了避免平凡解，一个重要的技巧是：在计算$e_{ji}$的损失函数时，对于$c_j$的计算，不要将$e_{ji}$本身加进去，新的$c_j$表达式如下，式中的$(-i)$表示排除$i$
    $$c_j^{(-i)}=\frac{1}{M-1}\sum _{m=1,m\ne i}^M{e}_{jm}$$
• 步骤总结
  • 对每一个batch，经过神经网络，得到嵌入码
  • 计算batch内每个说话人的中心点
  • 计算相似度矩阵
  • 根据相似度矩阵，计算每个嵌入码的损失函数，对batch内所有嵌入码的损失函数求和，得到一个batch的总损失
    
• 优点
  • 动态地挖掘困难样本，每次参数优化都有足够的监督信息
  • 训练时，神经网络前向推理次数，等于样本数，而不是排列组合数，比其他基于二值决策的损失函数更加高效

其他广义端到端损失函数

• Dynamic-additive-margin Softmax（DAM-Softmax）
• Angular Margin Centroid Loss（AMCL）

总结

损失函数	多说话人交叉熵	Pairwise Loss	Triplet Loss	End-to-End Loss	Generalized End-to-End Loss
输入	单个话语	两个话语	三个话语	$N+1$个话语	$N\times M$个话语
中心点使用	否	否	否	使用一个说话人的中心点	使用一个batch中所有说话人的中心点
实现方式	Softmax	BCE	对比	BCE	对比或Softmax